Trắc nghiệm Toán 10 Cánh diều Bài 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm (Phần 2) có đáp án
Trắc nghiệm Toán 10 Cánh diều Bài 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm (Phần 2) có đáp án (Thông hiểu)
-
807 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Sản lượng lúa (đơn vị là tạ) của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Phương sai của bảng số liệu trên là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có số trung bình cộng:
\(\begin{array}{l}\overline x = \frac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}}\\ = 22,1\end{array}\)
Phương sai:
\(\begin{array}{l}{s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_n}{{\left( {{x_n} - \overline x } \right)}^2}}}{n}\\ = \frac{{5.{{\left( {20 - 22,1} \right)}^2} + 8.{{\left( {21 - 22,1} \right)}^2} + 11.{{\left( {22 - 22,1} \right)}^2} + ...... + 6.{{\left( {24 - 22,1} \right)}^2}}}{{40}}\\ = 1,54\end{array}\)
Câu 2:
41 học sinh của một lớp kiểm tra chất lượng đầu năm thang điểm 30. Kết quả như sau:

Phương sai của bảng số liệu trên là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có số trung bình cộng:
\(\begin{array}{l}\overline x = \frac{{9.3 + 11.6 + 14.4 + 16.4 + 17.6 + 18.7 + 20.3 + 21.4 + 23.2 + 25.2}}{{41}}\\ \approx 16,61\end{array}\)
Phương sai:
\(\begin{array}{l}{s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_n}{{\left( {{x_n} - \overline x } \right)}^2}}}{n}\\ = \frac{{3.{{\left( {9 - 16,61} \right)}^2} + 6.{{\left( {11 - 16,61} \right)}^2} + ... + 2.{{\left( {25 - 16,61} \right)}^2}}}{{41}}\\ = 11,24\end{array}\)
Câu 3:
41 học sinh của một lớp kiểm tra chất lượng đầu năm thang điểm 30. Kết quả như sau:

Khoảng tứ phân vị của bảng số liệu trên là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Do cỡ mẫu n = 41. Nên ta có:
Tứ phân vị thứ hai bằng trung vị là: Q2 = 17 (số thứ tự thứ 21)
Tứ phân vị thứ nhất bằng trung vị của dãy số liệu có số thứ tự từ 1 đến 20, có 20 số liệu, do đó, Q1 = (14 + 14) : 2 = 14 (số thứ tự thứ 10 là 14 và số thứ tự thứ 11 là 14)
Tứ phân vị thứ ba bằng trung vị của dãy số liệu có số thứ tự từ 22 đến 41, có 20 số liệu, do đó, Q3 = (20 + 20) : 2 = 20 (số thứ tự thứ 31 là 20 và số thứ tự thứ 32 là 20)
Khoảng tứ phân vị là: ΔQ = Q3 – Q1 = 20 – 14 = 6.
Câu 4:
Điều tra về số học sinh của một trường THPT ta có bảng như sau:
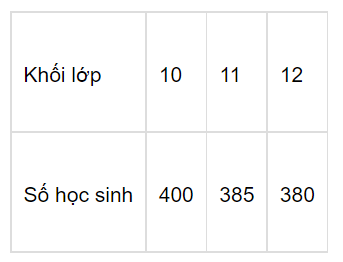
Phương sai của bảng số liệu trên là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có số trung bình cộng:
\(\overline x = \frac{{10.400 + 11.385 + 12.380}}{{400 + 385 + 380}} \approx 10,98\)
Phương sai:
\(\begin{array}{l}{s^2} = \frac{{{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_n}{{\left( {{x_n} - \overline x } \right)}^2}}}{n}\\ = \frac{{400{{\left( {10 - 10,98} \right)}^2} + 385{{\left( {11 - 10,98} \right)}^2} + 380{{\left( {12 - 10,98} \right)}^2}}}{{400 + 385 + 380}}\\ = 0,669\end{array}\)
Câu 5:
Điều tra về số học sinh của một trường THPT ta có bảng như sau:
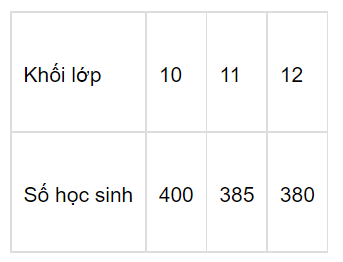
Khoảng tứ phân vị của bảng số liệu này là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Bảng số liệu trên có n = 400 + 385 + 380 = 1165.
Sắp xếp số liệu thành dãy không giảm và đánh số thứ tự từ 1 đến 1165
Tứ phân vị thứ hai bằng trung vị là: Q2 = 11 (số thứ tự thứ 583)
Tứ phân vị thứ nhất bằng trung vị của dãy số liệu có số thứ tự từ 1 đến 582, có 582 số liệu, do đó, Q1 = (10 + 10) : 2 = 10 (số thứ tự thứ 291 là 10 và số thứ tự thứ 292 là 10)
Tứ phân vị thứ ba bằng trung vị của dãy số liệu có số thứ tự từ 584 đến 1165, có 582 số liệu, do đó, Q3 = (12 + 12) : 2 = 12 (số thứ tự thứ 874 là 12 và số thứ tự thứ 875 là 12)
Khoảng tứ phân vị là: ΔQ = Q3 – Q1 = 12 – 10 = 2.
Câu 6:
Cho mẫu số liệu: {10; 8; 6; 2; 4}. Phương sai là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có số trung bình cộng:
\(\overline x = \frac{{10 + 8 + 6 + 2 + 4}}{5} = 6\).
Phương sai:
\(\begin{array}{l}{s^2} = \frac{{{{\left( {{x_1} - \overline x } \right)}^2} + {{\left( {{x_2} - \overline x } \right)}^2} + ... + {{\left( {{x_n} - \overline x } \right)}^2}}}{n}\\ = \frac{{{{\left( {10 - 6} \right)}^2} + {{\left( {8 - 6} \right)}^2} + ... + {{\left( {4 - 6} \right)}^2}}}{5}\\ = 8\end{array}\)
Câu 7:
Tốc độ phát triển của một loại virus trong 10 ngày với các điều kiện khác nhau (đơn vị: nghìn con) được thống kê lại như sau:
|
20 |
100 |
30 |
980 |
440 |
20 |
20 |
150 |
60 |
270 |
Khoảng tứ phân vị của mẫu số liệu trên là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Bảng số liệu trên có n = 10
Sắp xếp số liệu thành dãy không giảm ta có:
20; 20; 20; 30; 60; 100; 150; 270; 440; 980.
Tứ phân vị thứ hai bằng trung vị là: Q2 = (60 + 100) : 2 = 80 (số thứ tự thứ 5 là 60, số thứ tự thứ 6 là 100)
Tứ phân vị thứ nhất bằng trung vị của dãy số liệu: 20; 20; 20; 30; 60. Có 5 số liệu, do đó, Q1 = 20
Tứ phân vị thứ ba bằng trung vị của dãy số liệu 100; 150; 270; 440; 980. có 5 số liệu, do đó, Q3 = 270
Khoảng tứ phân vị là: ΔQ = Q3 – Q1 = 270 – 20 = 250 nghìn.
Câu 8:
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
|
Năng suất lúa (tạ/ha) |
25 |
30 |
35 |
40 |
45 |
|
Tần số |
4 |
7 |
9 |
6 |
5 |
Khoảng tứ phân vị của bảng số liệu trên là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Sắp thứ tự mẫu số liệu gồm n = 31 số liệu thành một dãy không giảm ta có:
25; 25; 25; 25; 30; 30; 30; 30; 30; 30; 30; 35; 35; 35; 35; 35; 35; 35; 35; 35; 40; 40; 40; 40; 40; 40; 45; 45; 45; 45; 45.
Tứ phân vị thứ hai Q2 là: 35
Q1 bằng trung vị của nửa dãy phía dưới (không bao gồm Q2) tức là trung vị của dãy số liệu: 25; 25; 25; 25; 30; 30; 30; 30; 30; 30; 30; 35; 35; 35; 35. Vậy Q1 = 30.
Q3 bằng trung vị của nửa dãy phía trên (không bao gồm Q2) tức là trung vị của dãy số liệu: 35; 35; 35; 35; 35; 40; 40; 40; 40; 40; 40; 45; 45; 45; 45. Vậy Q3 = 40.
Khoảng tứ phân vị là: ΔQ = Q3 – Q1 = 40 – 30 = 10.
