Trắc nghiệm Toán 10 CTST Bài tập cuối chương 7 (Vận dụng) có đáp án
-
796 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho f(x) = (m – 3)x2 + (m + 3)x – (m + 1). Để f(x) là một tam thức bậc hai và có nghiệm kép thì:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét f(x) = (m – 3)x2 + (m + 3)x – (m + 1).
Ta có:
∆ = (m + 3)2 – 4.(m – 3).[–(m + 1)]
= m2 + 6m + 9 + 4.(m – 3)(m + 1)
= m2 + 6m + 9 + 4(m2 – 2m – 3)
= 5m2 – 2m – 3.
Ta có f(x) là một tam thức bậc hai và có nghiệm kép khi và chỉ khi a ≠ 0 và ∆ = 0.
Vậy ta chọn phương án D.
Câu 2:
Cho f(x) = x2 + 2(m – 1)x + m2 – 3m + 4. Giá trị của m để f(x) không âm với mọi giá trị của x là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét f(x) = x2 + 2(m – 1)x + m2 – 3m + 4.
Ta có:
∆’ = (m – 1)2 – 1.(m2 – 3m + 4)
= m2 – 2m + 1 – m2 + 3m – 4
= m – 3.
Yêu cầu bài toán ⇔ Tìm m để f(x) ≥ 0 với mọi giá trị của x.
Ta có f(x) ≥ 0, với mọi giá trị của x.
⇔ a > 0 và ∆’ ≤ 0.
⇔ 1 > 0 (luôn đúng) và m – 3 ≤ 0.
⇔ m ≤ 3.
Vậy m ≤ 3 thỏa mãn yêu cầu bài toán.
Ta chọn phương án D.
Câu 3:
Cho f(x) = mx2 – 2mx + m – 1. Giá trị nào của m để f(x) ≥ 0 vô nghiệm?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Nếu m = 0 ta có f(x) = –1 < 0 khi đó f(x) ≥ 0 vô nghiệm.
Do đó m = 0 thỏa mãn yêu cầu đề bài.
Nếu m ≠ 0 thì f(x) = mx2 – 2mx + m – 1 là tam thức bậc hai.
Ta có:
∆’ = (–m)2 – m.(m – 1)
= m2 – m2 + m
= m.
Ta có f(x) ≥ 0 vô nghiệm. Nghĩa là, f(x) < 0, với mọi giá trị của x.
⇔ a < 0 và ∆’ < 0
⇔ m < 0 và m < 0
⇔ m < 0.
Vậy m ≤ 0 thỏa mãn yêu cầu bài toán.
Ta chọn phương án A.
Câu 4:
Tập hợp các giá trị của m để hàm số có tập xác định là ℝ là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số đã cho có tập xác định là ℝ khi và chỉ khi (2 – 3m)x2 + 2mx + m – 1 > 0 với mọi x ∈ ℝ.
Đặt f(x) = (2 – 3m)x2 + 2mx + m – 1.
Trường hợp 1: a = 0 ⇔ 2 – 3m = 0 ⇔ m = .
Với , ta có
.
Do đó không thỏa mãn.
Trường hợp 2: a ≠ 0.
Khi đó f(x) là tam thức bậc hai có:
∆’ = m2 – (2 – 3m)(m – 1)
= m2 – (–3m2 + 5m – 2)
= 4m2 – 5m + 2.
Để f(x) > 0 với mọi x ∈ ℝ thì a > 0 và ∆ < 0.
(1)
Ta giải bất phương trình 4m2 – 5m + 2 < 0 như sau:
Tam thức bậc hai g(m) = 4m2 – 5m + 2 có ∆ = (–5)2 – 4.4.2 = –7 < 0.
Do đó g(m) vô nghiệm.
Ta lại có am = 4 > 0.
Vì vậy g(m) > 0, với mọi giá trị của m ∈ ℝ.
Do đó không có giá trị nào của m thỏa mãn g(m) = 4m2 – 5m + 2 < 0.
Vì vậy không có giá trị nào của m để (1) thỏa mãn.
Kết hợp cả hai trường hợp, ta thu được m ∈ ∅.
Vậy ta chọn phương án C.
Câu 5:
Số giao điểm giữa đồ thị hàm số và đồ thị hàm số y = x – 3 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Phương trình hoành độ giao điểm của hai đồ thị là: .
Bình phương hai vế của phương trình trên, ta được 3x – 4 = (x – 3)2
⇒ 3x – 4 = x2 – 6x + 9
⇒ x2 – 9x + 13 = 0
⇒ hoặc .
Với , ta có (đúng)
Với , ta có (sai)
Vì vậy khi thay lần lượt và vào phương trình , ta thấy chỉ có thỏa mãn.
Vậy hai đồ thị cắt nhau tại một giao điểm.
Do đó ta chọn phương án D.
Câu 6:
Tổng bình phương các nghiệm của phương trình bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có
⇔ x – 2 = 0 hoặc
⇔ x = 2 hoặc (2)
Giải (2):
Bình phương hai vế của phương trình (2), ta được:
2x + 7 = (x + 2)2
⇒ 2x + 7 = x2 + 4x + 4
⇒ x2 + 2x – 3 = 0
⇒ x = 1 hoặc x = –3.
Với x = 1, ta có (đúng)
Với x = –3, ta có (sai)
Vì vậy khi thay lần lượt các giá trị x = 1 và x = –3 vào phương trình (2), ta thấy chỉ có x = 1 thỏa mãn.
Do đó phương trình (2) có nghiệm là x = 1.
Vậy phương trình đã cho có nghiệm là x = 2 hoặc x = 1.
Khi đó tổng bình phương các nghiệm của phương trình đã cho là: 22 + 12 = 5.
Vậy ta chọn phương án B.
Câu 7:
Lợi nhuận I thu được từ việc giảm giá một loại xe gắn máy của một doanh nghiệp tư nhân là một tam thức bậc hai I(x) = 200x2 – 1400x + 2400, trong đó x là số tiền giảm giá (triệu đồng) và 0 ≤ x ≤ 5. Với số tiền giảm giá là bao nhiêu thì doanh nghiệp đó không có lãi?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Tam thức bậc hai I(x) = 200x2 – 1400x + 2400 có:
∆’ = (–700)2 – 200.2400 = 10 000 > 0.
Suy ra I(x) có hai nghiệm phân biệt là:
Ta lại có a = 200 > 0 và 0 ≤ x ≤ 5.
Vì vậy ta có bảng xét dấu sau:

Theo bảng xét dấu ta có:
⦁ I(x) dương với mọi x thuộc hai khoảng [0; 3) và (4; 5];
⦁ I(x) âm với mọi x thuộc khoảng (3; 4);
⦁ I(x) = 0 khi x = 3 hoặc x = 4.
Do đó doanh nghiệp đó không có lãi khi và chỉ khi I(x) ≤ 0.
Tức là khi x ∈ [3; 4].
Hay ta có thể nói là khi cửa hàng giảm giá từ 3 đến 4 triệu đồng thì doanh nghiệp đó không có lãi.
Vậy ta chọn phương án B.
Câu 8:
Một mảnh đất hình chữ nhật có chu vi là 150 m. Để diện tích của mảnh đất đó lớn hơn 650 m2 thì chiều dài của mảnh đất phải:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Gọi x (m) là chiều dài của mảnh đất hình chữ nhật (x > 0).
Mảnh đất hình chữ nhật có chu vi là 150 m nên có nửa chu vi là 75 m.
Khi đó chiều rộng của mảnh đất là: 75 – x (m).
Do chiều dài luôn lớn hơn chiều rộng nên x > 75 – x hay x > 37,5.
Diện tích của mảnh đất là: x(75 – x) = –x2 + 75x (m2).
Theo đề ta có diện tích của mảnh đất đó lớn hơn 650 m2.
⇔ –x2 + 75x > 650.
+) Xét tam thức bậc hai f(x) = –x2 + 75x – 650 có:
∆ = 752 – 4.(–1).(–650) = 3025 > 0.
Suy ra f(x) có hai nghiệm phân biệt là:
Ta lại có a = –1 < 0 và x > 37,5 nên:
⦁ f(x) âm với mọi x thuộc hai khoảng (0; 37,5) và (65; +∞);
⦁ f(x) dương với mọi x thuộc khoảng (37,5; 65);
⦁ f(x) = 0 khi x = 37,5 hoặc x = 65.
Do đó bất phương trình –x2 + 75x – 650 ≥ 0 có tập nghiệm là [37,5; 65].
Khi đó chiều dài của mảnh đất phải từ 37,5 m đến 65 m thì diện tích của mảnh đất đó lớn hơn 650 m2.
Vậy ta chọn phương án D.
Câu 9:
Cho ∆MNP vuông tại M có MN dài hơn MP 10 cm. Biết chu vi của ∆MNP là 50 cm. Độ dài của cạnh NP bằng khoảng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Theo đề, ta có MN dài hơn MP 10 cm nên MN = MP + 10.
Xét ∆MNP vuông tại M có MN2 + MP2 = NP2 (Định lí Pythagore)
Suy ra (MP + 10)2 + MP2 = NP2
Hay MP2 + 20MP + 100 + MP2 = NP2
Do đó NP2 = 2MP2 + 20MP + 100
Nên
• Ta có chu vi của ∆MNP là 50 cm.
Suy ra: MN + NP + MP = 50.
Khi đó
(1)
Bình phương hai vế của phương trình trên ta được:
2MP2 + 20MP + 100 = 1600 – 160MP + 4MP2
Þ 2MP2 – 180MP + 1500 = 0
Þ MP ≈ 80,71 hoặc MP ≈ 9,29.
Thay lần lượt các giá trị trên vào phương trình (1), ta thấy chỉ có MP ≈ 9,29 thỏa mãn.
Do đó NP ≈ 21,41 cm.
Vậy ta chọn phương án A.
Câu 10:
Khoảng cách từ nhà An ở vị trí A đến nhà Bình là 200 m. Từ nhà, nếu An đi x mét theo phương tạo với AB một góc 120° thì sẽ đến nhà bác Mai ở vị trí M và nếu đi thêm 300 m nữa thì sẽ đến siêu thị ở vị trí S.
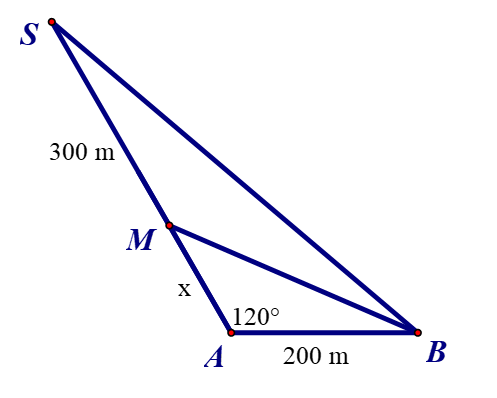
Biết rằng quãng đường từ nhà Bình đến siêu thị gấp đôi quãng đường từ nhà Bình đến nhà bác Mai. Khi đó quãng đường từ nhà An đến nhà bác Mai là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng định lí côsin cho ∆ABM, ta có:
BM2 = AM2 + AB2 – 2AM.AB.cosA
= x2 + 2002 – 2x.200.cos120°
= x2 + 40 000 + 200x
Do đó
Áp dụng định lí côsin cho ∆ABS, ta được:
BS2 = AS2 + AB2 – AS.AB.cosA
= (x + 300)2 + 2002 – 2.(x + 300).200.cos120°
= x2 + 600x + 90 000 + 40 000 + 200x + 60 000
= x2 + 800x + 190 000
Do đó
Theo bài, quãng đường từ nhà Bình đến siêu thị gấp đôi quãng đường từ nhà Bình đến nhà bác Mai nên ta có:
BS = 2BM.
(1)
Bình phương hai vế của phương trình (1), ta được:
x2 + 800x + 190 000 = 4(x2 + 200x + 40 000)
⇒ –3x2 + 30 000 = 0
⇒ x = 100 (thỏa mãn x > 0) hoặc x = –100 (không thỏa mãn).
Vậy ta chọn phương án C.
