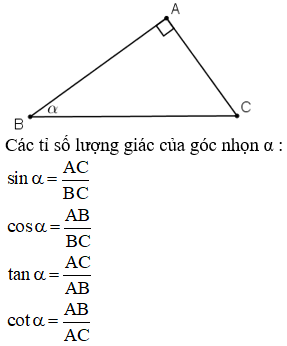
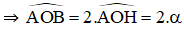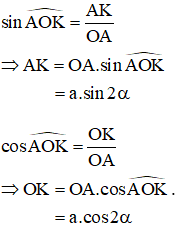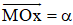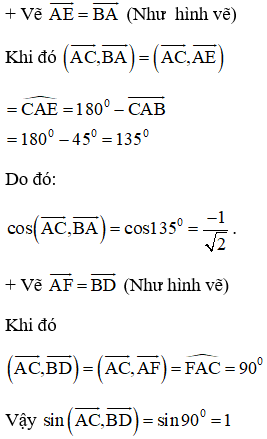Bài 1: Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ
-
1017 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Trả lời câu hỏi Toán 10 Hình học Bài 1 trang 38: Tìm các giá trị lượng giác của các góc 120o, 150o.
Xem đáp án
Các giá trị lượng giác của góc 120o là:
sin 120º = sin (180º – 60º) = sin 60º = √3/2.
cos 120º = cos(180º – 60º) = –cos 60º = –1/2
tan 120º = sin 120º / cos 120º = –√3
cot 120º = cos 120º / sin 120º = –1/√3
Các giá trị lượng giác của góc 150º là:
sin 150º = sin ( 180º – 30º ) = sin 30º = 1/2
cos 150º = –cos ( 180º – 30º ) = –cos 30º = (–√3)/2
tan 150º = sin 150º / cos 150º = –1/√3
cot 150º = cos 150º / sin 150º = –√3.
Câu 3:
Bài 1 (trang 40 SGK Hình học 10): Chứng minh rằng trong tam giác ABC có:
a) sin A = sin(B + C) ; b) cos A = -cos(B + C)
Xem đáp án
A, B , C là ba góc của ΔABC nên ta có: A + B + C = 180º
a) sin A = sin (180º – A) = sin (B + C)
b) cos A = – cos (180º – A) = –cos (B + C)
Câu 4:
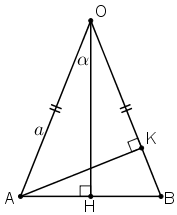
Bài 2 (trang 40 SGK Hình học 10):Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử = α. Tính AK và OK theo a và α.
Xem đáp án
ΔAOB cân tại O nên OH là đường cao đồng thời là đường phân giác
Xét ΔOAK vuông tại K có:
Câu 5:
Bài 3 (trang 40 SGK Hình học 10): Chứng minh rằng:
a) sin105º = sin75º;
b) cos170º = -cos10º;
c) cos122º = -cos58º.
Xem đáp án
(Áp dụng tính chất lượng giác của hai góc bù nhau)
a) sin 105º = sin (180º – 105º) = sin 75º ;
b) cos 170º = –cos (180º – 170º) = –cos 10º;
c) cos 122º = –cos (180º – 122º) = –cos 58º.
Kiến thức áp dụng
sin α = sin (180º – α)
cos α = –cos (180º – α)
Câu 6:
Bài 4 (trang 40 SGK Hình học 10): Chứng minh rằng với mọi góc α (0o ≤ α ≤ 180o) ta đều có cos2α + sin2α = 1.
Xem đáp án
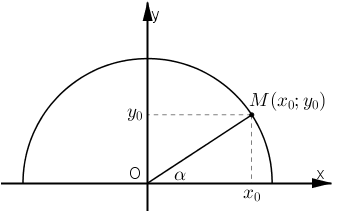
Vẽ đường tròn lượng giác (O; 1).
Với mọi α (0º ≤ α ≤ 180º) ta đều có điểm M(x0; y0) thuộc nửa đường tròn sao cho 
Khi đó ta có: sin α = y0 ; cos α = x0.
Mà M thuộc đường tròn lượng giác nên x02 + y02 = OM2 = 1⇒ sin2 α + cos2 α = 1
Câu 7:
Bài 5 (trang 40 SGK Hình học 10): Cho góc x, với cosx = . Tính giá trị của biểu thức: P = 3sin2x + cos2x.
Xem đáp án
Ta có : sin2 x + cos2 x = 1 ⇒ sin2 x = 1 – cos2 x.
⇒ P = 3.sin2 x + cos2 x
= 3.(1 – cos2x) + cos2 x
= 3 – 3.cos2x + cos2x
= 3 – 2.cos2x
= 3 – 2.()2
= 3 –
= .
Kiến thức áp dụng
Với mọi góc α (0º ≤ α ≤ 180º) : cos2α + sin2α = 1.
Câu 8:
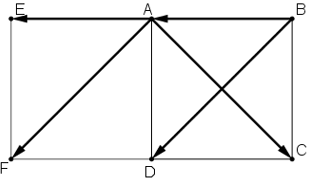
Bài 6 (trang 40 SGK Hình học 10): Cho hình vuông ABCD. Tính:
cos(, ), sin(,), cos(,)
Xem đáp án
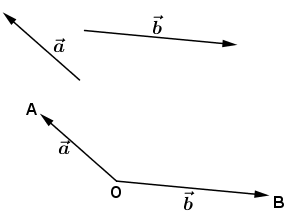
Để tính được góc giữa các vec tơ ta đưa chúng về các vec tơ chung gốc.
Kiến thức áp dụng
+ Để tính góc giữa hai vec tơ, ta đưa hai vec tơ về chung gốc.
+ Góc giữa hai vec tơ cùng hướng bằng 0º ; góc giữa hai vec tơ ngược hướng bằng 180º.