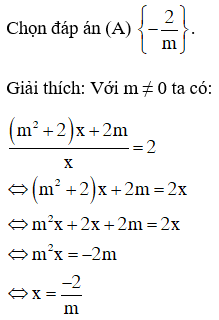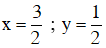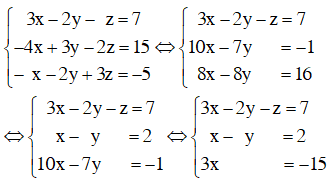Ôn tập chương 3
-
1192 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Khi nào hai phương trình được gọi là tương đương ? Cho ví dụ.
 Xem đáp án
Xem đáp án
- Hai phương trình có cùng tập nghiệm thì tương đương nhau.
- Ví dụ hai phương trình:
- 3x + 2 = 0 và (x - 1)(x - 2)(x2 + x + 1) = 0
là hai phương trình tương đương vì chúng có cùng tập nghiệm là {1, 2}.
Câu 2:
Thế nào là phương trình hệ quả ? Cho ví dụ.
 Xem đáp án
Xem đáp án
– Phương trình (a) có tập nghiệm là S1
Phương trình (b) có tập nghiệm là S2
Nếu S1 ⊂ S2 thì ta nói (b) là phương trình hệ quả của phương trình (a), kí hiệu: (a) ⇒ (b)
– Ví dụ : Phương trình x + 1 = 0 có tập nghiệm là S1 = {–1}
phương trình x2 – x – 2 = 0 có tập nghiệm là S2 = {–1; 2}
Ta có: S1 ⊂ S2 nên phương trình x2 – x – 2 = 0 là phương trình hệ quả của phương trình x + 1 = 0, kí hiệu:
x + 1 = 0 ⇒ x2 – x – 2 = 0.
Câu 3:
Giải các phương trình:
 Xem đáp án
Xem đáp án
a) Điều kiện: x - 5 ≥ 0 ⇔ x ≥ 5
⇔ x = 6 (thỏa mãn điều kiện xác định)
Vậy phương trình có nghiệm là: x = 6
b) Điều kiện xác định:
Xét x = 1: VT (2) = 1; VP (2) = 2.
Vậy x = 1 không phải nghiệm của (2) nên phương trình (2) vô nghiệm.
Vậy phương trình đã cho vô nghiệm.
c)
Điều kiện xác định: x – 2 > 0 ⇔ x > 2.
Khi đó (3) ⇔ = 8 ⇔ x = –2√2 (không t/m đkxđ)
hoặc x = 2√2 (t/m đkxđ)
Vậy phương trình có nghiệm là: x = 2√2.
d) Điều kiện xác định:
Vậy phương trình vô nghiệm.
Câu 4:
Giải các phương trình
 Xem đáp án
Xem đáp án
Quy đồng và bỏ mẫu chung ta được:
Phương trình (1) ⇔ (3x + 4)(x + 2) – (x – 2) = 4 + 3(x2 – 4)
⇔ 3 + 6x + 4x + 8 – x + 2 = 4 + 3 – 12
⇔ 9x = –18
⇔ x = –2 (không thỏa mãn đkxđ)
Vậy phương trình vô nghiệm.
Điều kiện xác định: 2x – 1 ≠ 0 ⇔ x ≠ 1/2.
Quy đồng và bỏ mẫu chung ta được:
Phương trình (2) ⇔ 2(3x2 – 2x + 3) = (2x – 1)(3x – 5)
⇔ 6 – 4x + 6 = 6 – 10x – 3x + 5
⇔ 9x = –1
⇔ x = –1/9 (thỏa mãn đkxđ)
Vậy phương trình có nghiệm là x = –1/9.
Điều kiện xác định x2 - 4 ≥ 0
Bình phương hai vế của phương trình ta được:
(3) ⇒ – 4 =
⇔ – 4 = – 2x + 1
⇔ 2x = 5 ⇔ x = 5/2 (thỏa mãn điều kiện xác định).
Thử lại thấy x = 5/2 là nghiệm của phương trình (3).
Vậy phương trình có nghiệm là x = 5/2.
Câu 5:
Giải các hệ phương trình
 Xem đáp án
Xem đáp án
a) (nhân pt1 với 2 rồi cộng với pt2 để giản ước x)
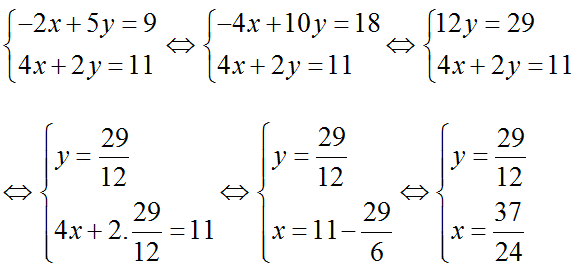
Vậy hệ phương trình có nghiệm là:

b) (nhân pt2 với 2 rồi cộng với pt1 để giản ước y)
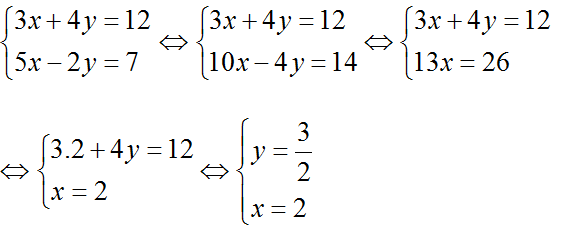
Vậy hệ phương trình có nghiệm là:
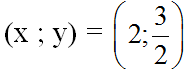
c) (nhân pt1 với 2, pt2 với 3 rồi cộng để giản ước y)
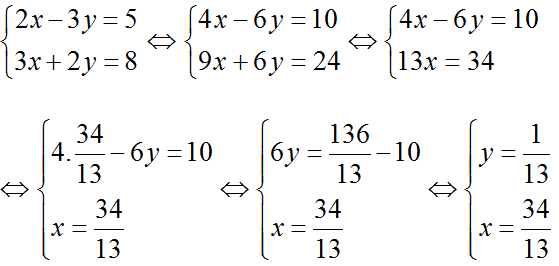
Vậy hệ phương trình có nghiệm là:
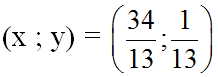
d) (nhân pt1 với 5, pt2 với 3 rồi cộng để giản ước y)
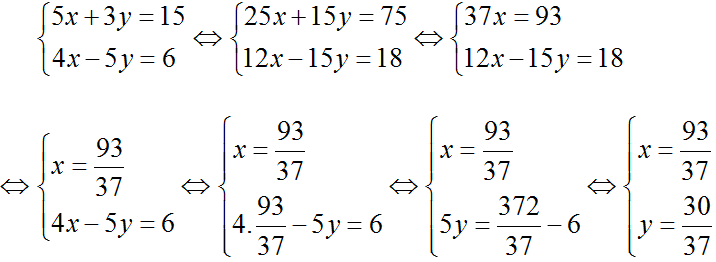
Vậy hệ phương trình có nghiệm là:
Câu 6:
Hai công nhân được giao việc sơn một bức tường. Sau khi người thứ nhất làm được 7 giờ và người thứ hai làm được 4 giờ thì họ sơn được 5/9 bức tường. Sau đó họ cùng làm việc với nhau trong 4 giờ nữa thì chỉ còn lại 1/18 bức tường chưa sơn. Hỏi nếu mỗi người làm riêng thì sau bao nhiêu giờ mỗi người mới sơn xong bức tường ?
 Xem đáp án
Xem đáp án
Gọi t1 (giờ) là thời gian người thứ nhất sơn xong bức tường,
t2 (giờ) là thời gian người thứ hai sơn xong bức tường.
(Điều kiện: t1 > 0; t2 > 0)
+ Trong một giờ:
+ Người thứ nhất làm trong 7 giờ và người thứ hai làm trong 4 giờ thì họ sơn được 5/9 bức tường nên ta có:
+ Sau đó họ cùng làm việc với nhau trong 4 giờ nữa, nghĩa là người thứ nhất làm trong 7 + 4 = 11 giờ và người thứ hai làm trong 4 + 4 = 8 giờ.
Khi đó họ còn 1/18 bức tường chưa sơn nghĩa là họ đã sơn được 17/18 bức tường.
Ta có phương trình
Ta có hệ phương trình
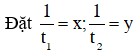
Giải hệ phương trình trên ta được
Vậy nếu mỗi người làm riêng thì người thứ nhất sơn xong bức tường trong 18 giờ, người thứ hai sơn xong bức tường trong 24 giờ.
Câu 7:
Giải các hệ phương trình
 Xem đáp án
Xem đáp án
a)
Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần các ẩn.
Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (3) với 4 rồi cộng với phương trình (2) ta được:
Vậy hệ phương trình có nghiệm
b)
Đưa hệ phương trình về dạng hệ tam giác bằng cách khử dần các ẩn.
Nhân phương trình (2) với 2 rồi cộng với phương trình (1) và cộng phương trình (2) với phương trình (3) ta được:
Giải hệ phương trình trên ta được
Vậy hệ phương trình có nghiệm
Câu 8:
Ba phân số đều có tử số là 1 và tổng của ba phân số đó bằng 1. Hiệu của phân số thứ nhất và phân số thứ hai bằng phân số thứ ba, còn tổng của phân số thứ nhất và phân số thứ hai bằng 5 lần phân số thứ ba. Tìm các phân số đó.
 Xem đáp án
Xem đáp án
Gọi các phân số cần tìm là x, y, z.
Tổng của ba phân số bằng 1 nên:
x + y + z = 1 (1)
Hiệu của phân số thứ nhất và thứ hai bằng phân số thứ ba nên:
x - y = z (2)
Tổng của phân số thứ nhất và thứ hai bằng 5 lần phân số thứ ba nên:
x + y = 5z (3)
Từ (1), (2), (3) ta có hệ:
Vậy ba phân số cần tìm lần lượt là:
Câu 9:
Một phân xưỏng được giao sản xuất 360 sản phẩm trong một số ngày nhất định. Vì phân xưởng tăng năng suất, mỗi ngày làm thêm được 9 sản phẩm so với định mức, nên trước khi hết thời hạn một ngày thì phân xưởng đã làm vượt số sản phẩm được giao là 5%. Hỏi nếu vẫn tiếp tục làm việc với năng suất đó thì khi đến hạn phân xưởng làm được tất cả bao nhiêu sản phẩm ?
 Xem đáp án
Xem đáp án
Gọi x (ngày) là số ngày dự định làm xong kế hoạch (x > 0).
Khi đó:
Số sản phẩm dự định làm trong một ngày là: 360/x (sản phẩm)
Thực tế, mỗi ngày làm thêm được 9 sản phẩm nên năng suất thực tế là: 360/x + 9 (sản phẩm / ngày)
Số ngày làm thực tế là: x – 1 (ngày)
Số sản phẩm làm được trong x – 1 ngày là: 360 + 360.5% = 378 sản phẩm.
Ta có phương trình:
⇔ x = 8 (thỏa mãn) hoặc x = –5 (loại)
Số ngày dự định là 8 ngày, năng suất thực tế là 360:8 + 9 = 54 sản phẩm/ngày
Vậy khi đến hạn, phân xưởng sẽ làm được 54.8 = 432 sản phẩm.
Câu 10:
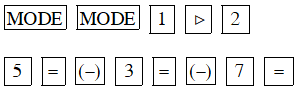
Giải các phương trình sau bằng máy tính bỏ túi
a) - 3x - 7 = 0 ; b) + 4x + 1 = 0;
c) + 1,2x - 1 = 0 ; d) + 5x + √8 = 0
 Xem đáp án
Xem đáp án
a) – 3x – 7 = 0
Màn hình hiện x1 = 1,520655562
Ấn tiếp 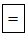
Vậy nghiệm gần đúng của phương trình là: x1 = 1,52; x2 = –0,92
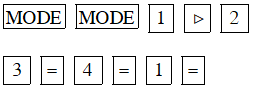
b) + 4x + 1 = 0
Màn hình hiện x1 = –0.3333333333
Ấn tiếp 
Vậy nghiệm gần đúng của phương trình là: x1 = –0,33; x2 = –1
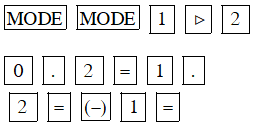
c) + 1,2x – 1 = 0
Màn hình hiện x1 = 0.7416573868
Ấn tiếp 
Vậy nghiệm gần đúng của phương trình là: x1 = 0,74; x2 = –6,74
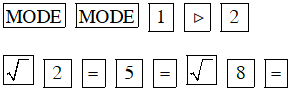
d) + 5x + √8 = 0
Màn hình hiện x1 = –0.7071067812
Ấn tiếp 
Vậy nghiệm gần đúng của phương trình là: x1 = –0,71 ; x2 = –2,83
* Đối với máy tính CASIO fx–570 các loại
Thay vì ấn 
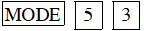
* Đối với máy tính VINACAL
Thay vì ấn 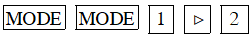

Câu 11:
Giải các phương trình
a) |4x - 9| = 3 - 2x ; b) |2x + 1| = |3x + 5|
 Xem đáp án
Xem đáp án
a) |4x – 9| = 3 – 2x (1)
+ Xét 4x – 9 ≥ 0 ⇔ x ≥ 9/4, khi đó |4x – 9| = 4x – 9
(1) trở thành 4x – 9 = 3 – 2x ⇔ 6x = 12 ⇔ x = 2 < 9/4 (không thỏa mãn).
+ Xét 4x – 9 < 0 ⇔ x < 9/4, khi đó |4x – 9| = 9 – 4x
(1) trở thành 9 – 4x = 3 – 2x ⇔ 2x = 6 ⇔ x = 3 > 9/4 (không thỏa mãn).
Vậy phương trình vô nghiệm.
b) |2x + 1| = |3x + 5|
Vậy phương trình đã cho có tập nghiệm là
Câu 12:
Tìm hai cạnh của một mảnh vườn hình chữ nhật trong hai trường hợp
a) Chu vi là 94,4 m và diện tích là 494,55 .
b) Hiệu của hai cạnh là 12,1 m và diện tích là 1089 .
 Xem đáp án
Xem đáp án
Gọi chiều dài, chiều rộng của mảnh vườn hình chữ nhật lần lượt là x (m), y (m). (điều kiện x > y > 0)
a) Theo đề bài:
Chu vi là 94,4m nên ta có phương trình: 2(x + y) = 94,4 (1)
Diện tích là 494,55m2 nên ta có phương trình: x.y = 494,55 (2)
Từ (1) và (2) ta có hệ:
Giải hệ phương trình trên:
Cách 1: Dựa vào định lý Vi–et đảo
Từ hệ phương trình suy ra x, y là nghiệm của phương trình:
– 47,2X + 494,55 = 0
Giải phương trình ta được: X1 = 31,5 và X2 = 15,7
Vì x > y nên x = 31.5 và y = 15.7
Cách 2: Phương pháp thế
Từ x + y = 47,2 ⇒ x = 47,2 – y, thay vào phương trình x.y = 494,55 ta được:
(47,2 – y).y = 494,55
⇔ 47,2.y – = 494,55
⇔ – 47,2y + 494,55 = 0
⇔ y = 31.5 hoặc y = 15.7
Nếu y = 31.5 ⇒ x = 15.7 (loại vì x < y)
Nếu y = 15.7 ⇒ x = 31.5 (thỏa mãn).
Vậy hình chữ nhật có chiều dài bằng 31.5m và chiều rộng bằng 15.7m
Hiệu của hai cạnh là 12,1 m nên ta có phương trình: x – y = 12,1 (3)
Diện tích là 1089m2 nên ta có phương trình: x.y = 1089 (4)
Từ (3) và (4) ta có hệ:
Từ (3) ⇒ x = 12,1 + y, thay vào (4) ta được:
(12,1 + y).y = 1089
⇔ + 12,1.y – 1089 = 0
⇔ y = 27,5 (t/m) hoặc y = –39,6 (loại)
⇒ x = 12,1 + 27,5 = 39,6
Vậy hình chữ nhật có chiều dài 39,6m và chiều rộng 27,5m
Câu 13:
Hai người quét sân. Cả hai người cùng quét sân hết 1 giờ 20 phút, trong khi nếu chỉ quét một mình thì người thứ nhất quét hết nhiều hơn 2 giờ so với người thứ hai. Hỏi mỗi người quét sân một mình hết mấy giờ?
 Xem đáp án
Xem đáp án
– Gọi x (giờ) là thời gian người thứ nhất quét sân một mình (x > 2).
– Khi đó, x – 2 (giờ) là thời gian người thứ hai quét sân một mình.
– Trong 1 giờ:
Người thứ nhất quét được 1/x (sân)
Người thứ hai quét được 1/(x – 2) (sân)
Cả hai người quét được 1/x + 1/(x – 2) (sân).
– Lại theo đề bài: Cả hai người cùng quét sân hết 1 giờ 20 phút = 4/3 giờ nên trong một giờ, cả hai người quét được 3/4 sân.
Vậy ta có phương trình:
Vậy nếu quét một mình thì người thứ nhất quét hết 4 giờ, người thứ hai hết 2 giờ.
Câu 16:
Chọn phương án đúng trong các bài tập sau
Nghiệm của hệ phương trình là
 Xem đáp án
Xem đáp án
Chọn đáp án (C) .
Giải thích : Các bạn có thể sử dụng máy tính cầm tay, hoặc sử dụng phương pháp cộng đại số hoặc thế để giải hệ phương trình.
Hệ phương trình có nghiệm
Vì 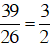
Câu 17:
Chọn phương án đúng trong các bài tập sau
Nghiệm của hệ phương trình
 Xem đáp án
Xem đáp án
– Chọn đáp án (D) (–5; –7; –8)
– Giải thích: Các bạn có thể sử dụng máy tính cầm tay để giải ra nghiệm hoặc giải bằng cách đưa về hệ dạng tam giác như sau:
Giải hệ phương trình trên ta được x = –5 ; y = –7 ; z = –8.
Vậy hệ phương trình có nghiệm (x ; y ; z) = (–5 ; –7 ; –8)


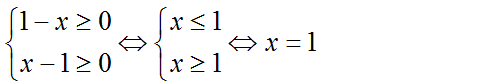
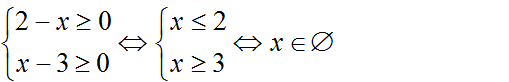
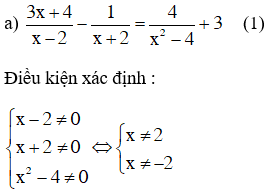
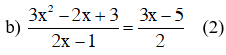
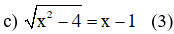
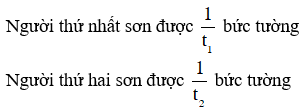
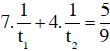
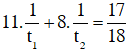
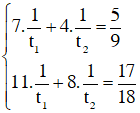
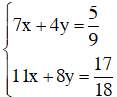
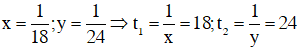
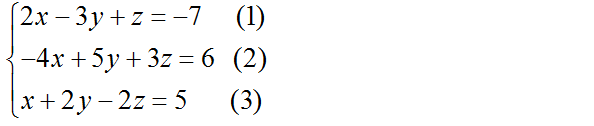
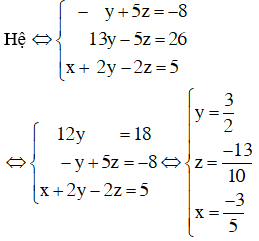
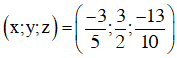
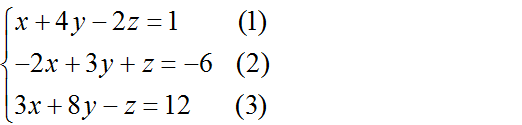
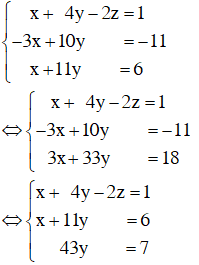
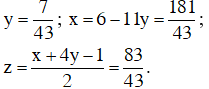
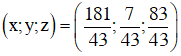
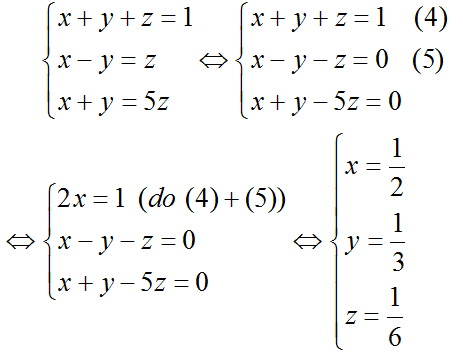
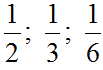
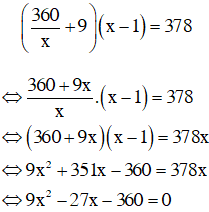
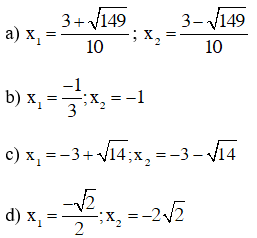
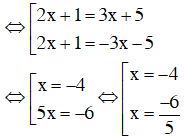
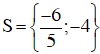
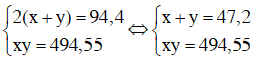
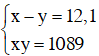
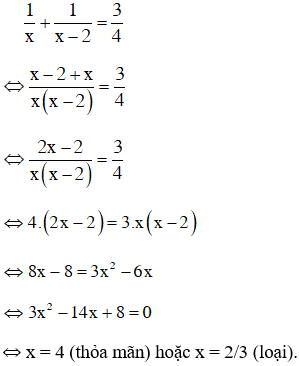

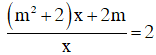 trong trường hợp m ≠ 0 là
trong trường hợp m ≠ 0 là