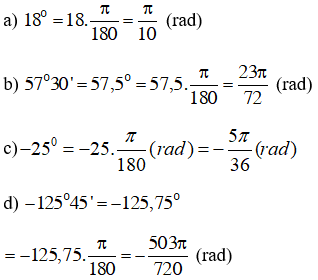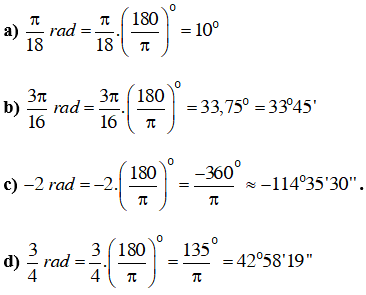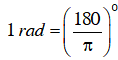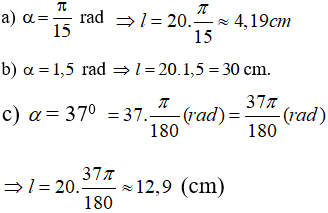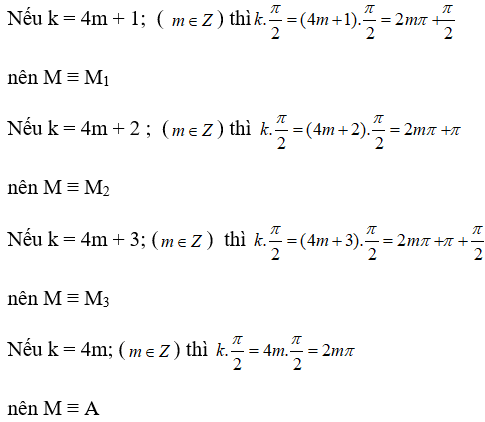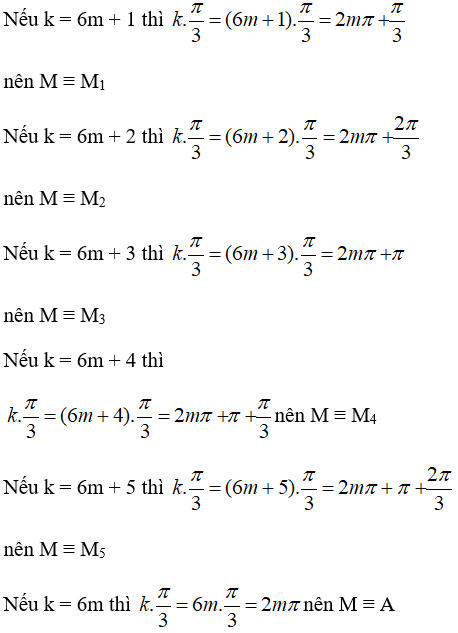Bài 1: Cung và góc lượng giác
-
1271 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Sử dụng máy tính bỏ túi để đổi từ độ sang radian và ngược lại.
a) Đổi 35o47’25’’ sang radian
b) Đổi 3 rad ra độ
Xem đáp án
a) Đổi 35o47’25’’ sang radian
b) Đổi 3 rad ra độ
Câu 3:
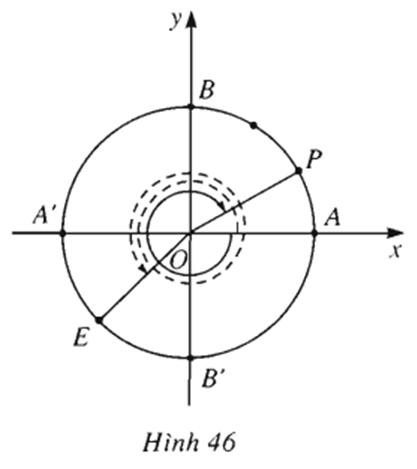
Tìm số đo của các góc lượng giác (OA, OE) và (OA, OP) trên hình 46 (điểm E là điểm chính giữa của cung (A'B'), sđ cung AP = sđ cung AB). Viết số đo này theo đơn vị radian và theo đơn vị độ.
Xem đáp án
(OA, OE) = sđ cung(AE) = sđ cung(AB') + sđ cung(B'E) = - 90o + (-45)o = -135o = -3/4(rad)
(OA, OP) = sđ cung(AP)= 1/3 sđ cung(AB) = 1/3 . 90° = 30o = /6 rad.
Câu 4:
Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không ? Khi nào trường hợp này xảy ra ?
Xem đáp án
Khi số đo hai cung lệch nhau k.2π (k ∈ Z) thì điểm cuối của chúng có thể trùng nhau.
Chẳng hạn các cung α = π/3 và β = π/3 + 2π , γ = π/3 - 2π có điểm cuối trùng nhau khi biểu diễn trên đường tròn lượng giác.
Câu 6:
Đổi số đo của các cung sau đây ra độ, phút, giây:
a.
b.
c. - 2
d.
Xem đáp án
Kiến thức áp dụng:
Câu 7:
Một đường tròn có bán kính 20cm. Tìm độ dài các cung trên đường tròn có số đo
a.
b. 1,5
c.
Xem đáp án
Từ công thức l = Rα (α có đơn vị là rad) ta có:
Kiến thức áp dụng:
Cung có số đo α rad của đường tròn bán kính R có độ dài: l = R.α
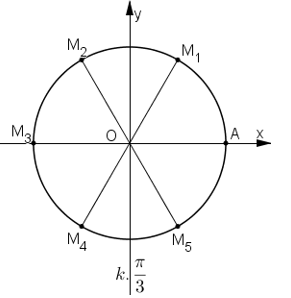
Câu 9:
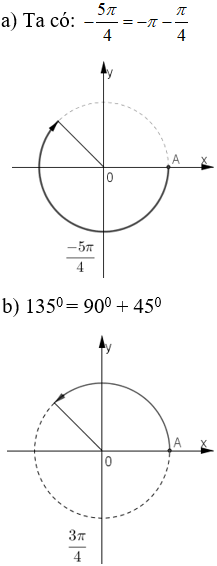
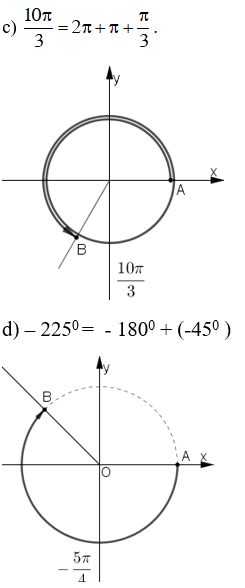
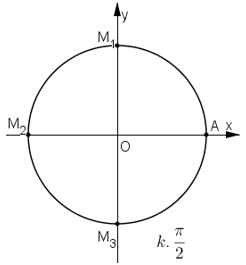
Trên đường tròn lượng giác gốc A, xác định các điểm M khác nhau biết rằng cung AM có số đo tương ứng là (trong đó k là một số nguyên tùy ý)
a.
b.
c.
Xem đáp án
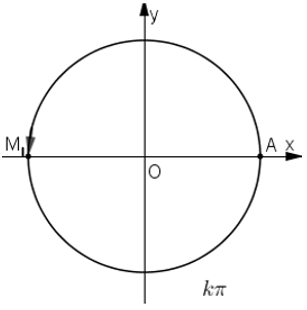
a) Nếu k = 2n +1 (n ∈ Z) (thì kπ = (2n + 1)π = 2nπ + π nên M ≡ M1
Nếu k = 2n (n ∈ Z) thì kπ = 2nπ nên M ≡ A
b)
c)
