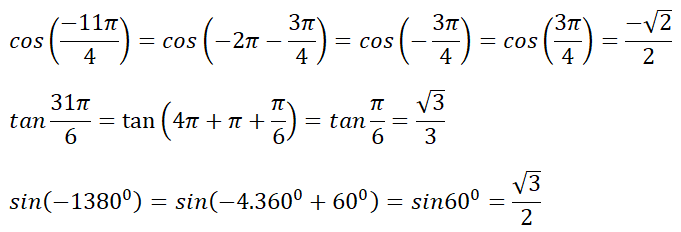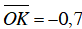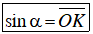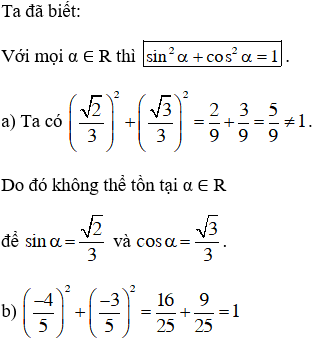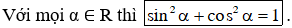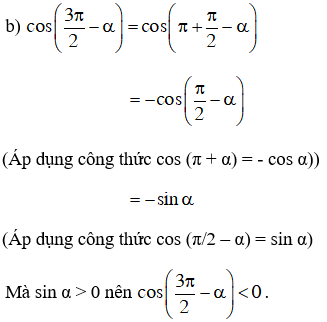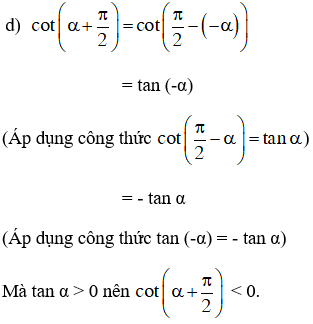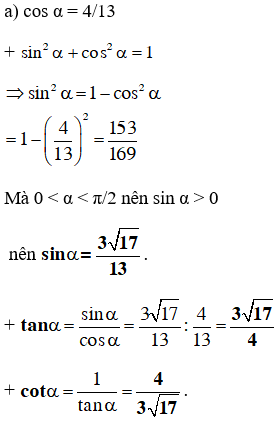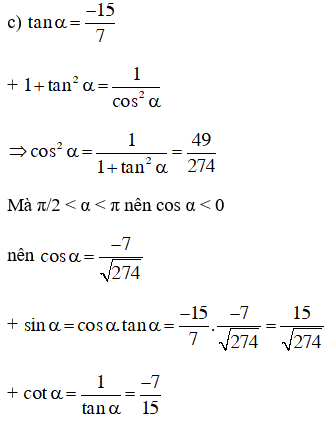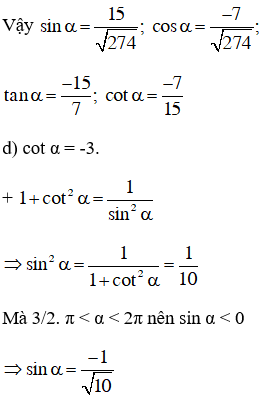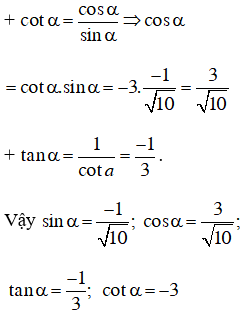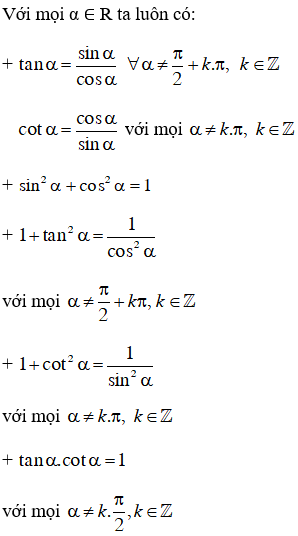Bài 2: Giá trị lượng giác của một cung
-
1269 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Nhắc lại khái niệm giá trị lượng giác của góc α, 0o ≤ α ≤ 180o.
Xem đáp án
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
Câu 2:
Tính , cos(-240o), tan(-405o).
Xem đáp án
sin 25π/4 = sin(6π + π/4) = sin π/4 =
cos(-240°) = cos(-360° + 120°) = cos 120°= - 1/2
tan(-405o) = tan(-360o - 45o) = -tan45o = -1
Câu 3:
Từ định nghĩa của sinα và cosα, hãy phát biểu ý nghĩa hình học của chúng.
Xem đáp án
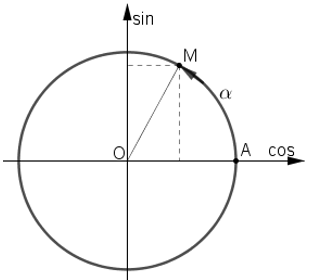
Xét điểm M thuộc đường tròn lượng giác xác định bởi số α .
Gọi H và K theo thứ tự là hình chiếu vuông góc của điểm M trên trục Ox và Oy. Khi đó:
cosα = OH¯; sinα = OK¯
Trong lượng giác, người ta gọi trục Ox là trục cô sin và trục Oy là trục sin .
Câu 4:
Từ ý nghĩa hình học của tanα và cotα hãy suy ra với mọi số nguyên k, tan(α + kπ) = tanα, cot(α + kπ) = cotα.
Xem đáp án
Trên đường tròn lượng giác,từ A(1,0) vẽ tiếp tuyến t’At với đường tròn lượng giác.
Từ B(0,1) vẽ tiếp tuyến s’Bs với đường tròn lượng giác .
Cho cung lượng giác AM có số đo α (α ≠ π/2 + kπ ). Gọi T là giao điểm của OM với trục t’At.
Gọi S là giao điểm của OM và trục s’Bs.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm T trên trục tan. Do đó
tan(α + kπ) = tanα.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm S trên trục cot. Do đó
cot(α + kπ) = cotα.
Câu 6:
Có cung α nào mà sinα nhận các giá trị tương ứng sau đây không ?
a.
b.
c.
d.
Xem đáp án
Ta có: -1 ≤ sin α ≤ 1 với mọi α ∈ R.
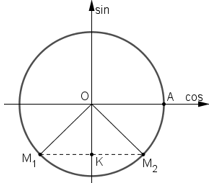
a) Vì -1 < –0,7 < 1 nên tồn tại cung α thỏa mãn sin α = -0,7.
Trên trục tung xác định điểm K sao cho 
Từ K kẻ đường thẳng vuông góc với trục tung cắt đường tròn lượng giác tại hai điểm M1 và M2.
Khi đó với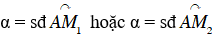 
thì theo định nghĩa sin α =
b) Vì 4/3 > 1 nên không tồn tại α để sin α = 4/3.
c) Vì -√2 < -1 nên không tồn tại α để sin α = -√2.
d) Vì √5/2 > 1 nên không tồn tại α để sin α = √5/2
Kiến thức áp dụng
+ Định nghĩa sin của cung α:
Cung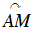 
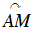
có sđ = α. K là hình chiếu của điểm M trên trục tung.
Khi đó ta định nghĩa 
(
là độ dài đại số của OK và chính là tung độ của điểm M).
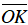
+ Với mọi α ∈ R thì -1 ≤ sin α ≤ 1.
Câu 8:
Cho 0 < α < . Xác định dấu của các giá trị lượng giác
a.
b.
c.
d.
Xem đáp án
Vì 0 < α < π/2 nên sin α > 0, cos α > 0, tan α > 0, cot α > 0.
Cách 1: Dựa vào mối quan hệ giữa các giá trị lượng giác của các cung có liên quan đặc biệt
a) sin (α – π) = - sin (π – α) (Áp dụng công thức sin (- α) = - sin α)
= -sin α (Áp dụng công thức sin (π – α) = sin α)
Mà sin α > 0 nên sin (α – π) < 0.
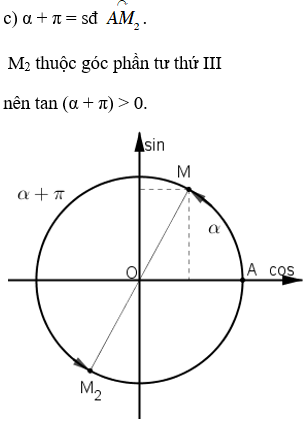
c) tan (α + π) = tan α.
Mà tan α > 0 nên tan (α + π) > 0.
Cách 2: Dựa vào biểu diễn cung trên đường tròn lượng giác:
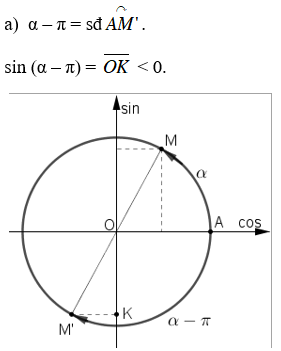
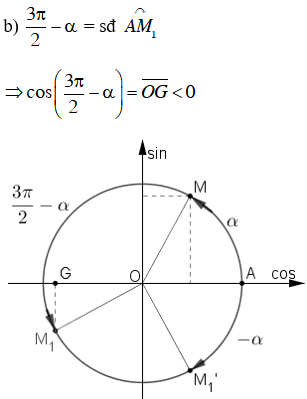
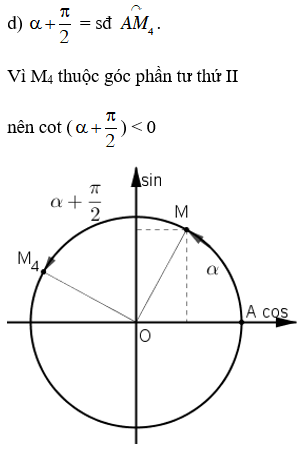
Vì 0 < α < π/2 nên ta biểu diễn α = sđ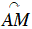 
như trên hình vẽ.
Câu 10:
Tính α, biết:
a.
b.
c.
d.
e.
f.
Xem đáp án
a) cos α = 1 ⇔ M trùng với A hay α = k.2π, k ∈ Z.
b) cos α = -1 ⇔ M trùng với A’ hay α = π + k.2π, k ∈ Z
c) cos α = 0 ⇔ M trùng với B hoặc B’ hay α = π/2 + k.π, k ∈ Z
d) sin α = 1 ⇔ M trùng với B hay α = π/2 + k.2π, k ∈ Z
e) sin α = -1 ⇔ M trùng với B’ hay α = -π/2 + k.2π, k ∈ Z
f) sin α = 0 ⇔ M trùng với A hoặc A’ hay α = k.π, k ∈ Z