Trắc nghiệm Hàm số y= ax +b có đáp án (Vận dụng)
-
2738 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho điểm M (m − 1; 2m + 1), điểm M luôn nằm trên đường thẳng cố định nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Ta có
Suy ra
Suy ra quỹ tích điểm M là đường thẳng 2x – y + 3 = 0
Câu 2:
Tìm m ∈ Z để hai đường thẳng y = mx + 1 (d1) và y = 2x + 3 (d2) cắt nhau tại một điểm có tọa độ nguyên.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Hoành độ giao điểm hai đường thẳng (d1) và (d2) là nghiệm của phương trình:
mx + 1 = 2x + 3 ⇔ (m − 2) x = 2 ⇔
Tọa độ giao điểm là số nguyên khi và chỉ khi nhận giá trị nguyên.
Từ đây suy ra (m − 2) ∈ Ư(2) ={±1 ;±2}
Với m – 2 = −1 ⇒ m = 1
Với m – 2 = 1 ⇒ m = 3
Với m – 2 = 2 ⇒ m = 4
Với m – 2 = −2 ⇒ m = 0
Vậy m ∈ {0; 1; 3; 4}.
Câu 3:
Biết rằng đường thẳng d: y = ax + b đi qua điểm M (4; -3) và song song với đường thẳng . Tính giá trị biểu thức a2 + b3
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Vì đường thẳng (d) song song với đường thẳng nên hệ số góc
Suy ra (d) có dạng (b 1)
Điểm M (4; -3) thuộc (d) nên tọa độ điểm M phải thỏa mãn đẳng thức
(tm)
Do đó
Câu 4:
Tìm m để giá trị lớn nhất của hàm số y = 2x + m2 − 1 trên đoạn [1; 3] bằng 5.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Trước hết nhận xét rằng: 2 > 0 nên hàm số đã cho đồng biến trên [1; 3].
Với 1 ≤ x1 < x2 ≤ 3 ⇒ y(1) ≤ y(x1) < y(x 2) ≤ y(3) nên giá trị lớn nhất của hàm số đã cho đạt được tại x = 3
Khi đó ymax = y(3) = 2.3+ m2 − 1= 5 + m2
Để ymax = 5 thì 5 + m2 = 5 ⇔ m = 0
Câu 5:
Viết phương trình đường thẳng d đi qua điểm A(-1; -5) và tạo với trục Ox một góc bằng 120°
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Vì đường thẳng (d) tạo với trục Ox một góc 120° nên hệ số góc k của đường thẳng (d) là k = tan120° = −
Suy ra phương trình đường thẳng (d) có dạng y = −x + b.
Lại có A ∈ (d) nên có đẳng thức −5 = (−1) + b ⇔ b= − − 5
Với b = − − 5 thì d: y = −x −− 5
Câu 6:
Tìm phương trình đường thẳng d: y = ax + b. Biết đường thẳng d đi qua điểm I (2; 3) và tạo với hai tia Ox, Oy một tam giác vuông cân.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Đường thẳng d: y = ax + b đi qua điểm I (2; 3) ⇒ 3 = 2a + b (∗)
Ta có: d ∩ Ox = A(−; 0); d ∩ Oy = B (0; b)
Suy ra OA= = − và OB = |b| = b (do A, B thuộc hai tia Ox, Oy).
Tam giác OAB vuông tại O. Do đó, ΔOAB vuông cân khi OA = OB
⇒ − = b ⇔
Với b = 0 ⇒ A ≡ B ≡ O (0; 0): không thỏa mãn.
Với a = −1, kết hợp với (∗) ta được hệ phương trình
Vậy đường thẳng cần tìm là d: y = −x + 5.
Câu 7:
Đường thẳng d: đi qua điểm M (-1; 6) tạo với các tia Ox, Oy một tam giác có diện tích bằng 4. Tính S = a + 2b
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Đường thẳng d: đi qua điểm M (−1; 6)⇒ (1)
Ta có d ∩ Ox = A (a; 0); d ∩ Oy = B (0; b).
Suy ra OA = |a| = a và OB = |b| = b (do A, B thuộc hai tia Ox, Oy).
Tam giác OAB vuông tại O. Do đó, ta có S ABC = OA.OB = 4 ⇒ ab = 4 (2)
Từ (1) và (2) ta có hệ
Do A thuộc tia Ox ⇒ a = 2. Khi đó, b = 6a – 8 = 4. Suy ra a + 2b = 10
Câu 8:
Cho hai điểm A, B thỏa mãn hệ phương trình . Tìm m để đường thẳng AB cắt đường thẳng y = x + m tại điểm C có tọa độ thỏa mãn yC =
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Phương trình đường thẳng AB là x + y – 1 = 0 hay y = 1 – x.
Hoành độ giao điểm C là nghiệm của phương trình
1 – x = x + m ⇔
Suy ra
Ta có
⇔ 2 + 2m = m2 − 2m + 1
⇔ m2 − 4m – 1 = 0
⇔ m = 2 ±
Câu 9:
Cho hàm số bậc nhất y = ax + b. Tìm a và b, biết rằng đồ thị hàm số cắt đường thẳng Δ1: y = 2x + 5 tại điểm có hoành độ bằng −2 và cắt đường thẳng Δ2: y = −3x + 4 tại điểm có tung độ bằng −2.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Với x = −2 thay vào y = 2x + 5, ta được y = 1.
Đồ thị hàm số cắt đường thẳng Δ1 tại điểm có hoành độ bằng −2 nên đi qua điểm A (−2; 1). Do đó ta có 1 = a.(−2) + b (1)
Với y = −2 thay vào y = −3x + 4, ta được x = 2.
Đồ thị hàm số cắt đường thẳng y = −3x + 4 tại điểm có tung độ bằng −2 nên đi qua điểm B (2; −2).
Do đó ta có −2 = a.2 + b. (2)
Từ (1) và (2), ta có hệ
Câu 10:
Tìm tất cả các giá trị của m để phương trình |x + 1| + |x − 1| = m2 − 2 có hai nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Đặt và có đồ thị chính là phần đường thẳng màu xanh
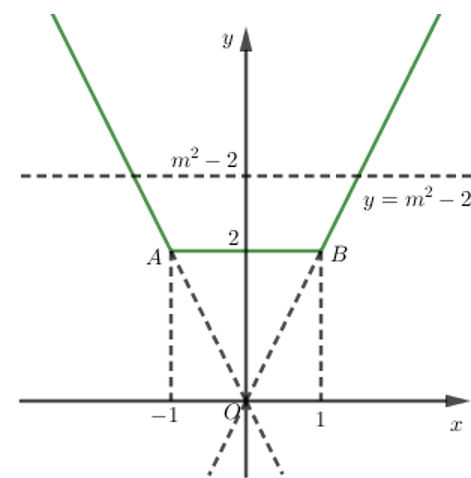
Đường thẳng d: y = m2 − 2 song song với trục hoành.
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số
và đường thẳng d: y = m2 − 2.
Nhìn vào đồ thị ta thấy đường thẳng y = m2 − 2 chỉ cắt đồ thị hàm số (đường màu xanh) tại 2 điểm phân biệt khi m2 – 2 > 2
Hay phương trình đã cho có hai nghiệm phân biệt khi
m2 – 2 > 2 m2 > 4 ⇔
Câu 11:
Hàm số y = x + |x + 1|có đồ thị là
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
- Ta có
- Vẽ đồ thị hàm số
+ Vẽ đồ thị hàm số y = 2x + 1 và y = -1 trên cùng một hệ trục tọa độ.
+ Giữ nguyên phần đồ thị y = 2x + 1 bên phải đường thẳng x = -1 và xóa phần bên trái.
+ Giữ nguyên phần đồ thị y = - 1 bên trái đường thẳng x = -1 và xóa phần bên phải.
Khi đó ta có đồ thị sau:
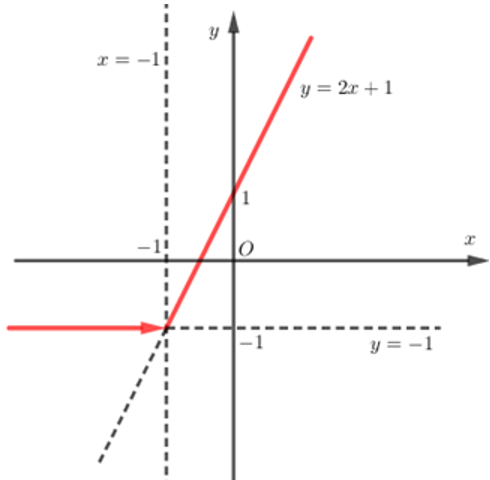
Câu 12:
Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng
d: (m 0) nhỏ nhất.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Gọi A và B lần lượt là giao điểm của đường thẳng (d) với trục Ox, Oy
Khi đó,
Gọi H là hình chiếu của O lên đường thẳng (d) thì OH chính là khoảng cách từ điểm O tới đường thẳng (d)
Xét tam giác vuông OAB có
Suy ra
Ta có
Theo bất đẳng thức Cauchy-Schwarz thì
Vậy OHmin = và đạt được khi m = -1
Câu 13:
Tìm phương trình đường thẳng d: y = ax + b. Biết đường thẳng d đi qua điểm I (1; 3), cắt hai tia Ox, Oy và cách gốc tọa độ một khoảng bằng .
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Đường thẳng d: y = ax + b đi qua điểm (1)
Ta có
Suy ra và (do A, B thuộc hai tia Ox, Oy)
Gọi H là hình chiếu vuông góc của O trên đường thẳng d
Xét tam giác AOB vuông tại O, có đường cao OH nên ta có
(2)
Từ (1) suy ra b = 3 – a. Thay vào (2), ta được (3-a)2 = 5a2 + 5
Với suy ra Suy ra Loại
Với a = -2, suy ra b = 5. Vậy đường thẳng cần tìm là d: y = -2x + 5
Câu 14:
Tìm giá trị thực của tham số m để ba đường thẳng y = 2x, y = −x − 3 và y = mx + 5 phân biệt và đồng qui.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Tọa độ giao điểm A của hai đường thẳng y = 2x và y = −x − 3 là nghiệm của hệ
Để ba đường thẳng đồng quy thì đường thẳng y = mx + 5 đi qua A
⇒ −2 = −1.m + 5 ⇒ m = 7.
Thử lại, với m = 7 thì ba đường thẳng y = 2x; y = −x – 3; y = 7x + 5 phân biệt và đồng quy.
Câu 15:
Cho hàm số y = 2(m−1)x – m2 – 3 (d). Tìm tất cả các giá trị của m để (d) cắt trục hoành tại một điểm có hoành độ x0 thỏa mãn x0 < 2.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Thấy rằng m ≠ 1 vì nếu m = 1 thì đường thẳng (d) suy biến thành y = –4 có đồ thị song song với trục hoành và không cắt trục hoành.
Phương trình hoành độ giao điểm của (d) và trục hoành là:
2 (m−1) x – m2 – 3 = 0 ⇒
Do x < 2 nên
⇔ m – 1 < 0 ⇔ m < 1
(Vì m2 − 4m + 7 = (m − 2)2 + 3 > 0 ∀m)
