15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hàm số y= ax +b có đáp án (Thông hiểu)

Câu 1:

Cho hàm số bậc nhất y = ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5.

A. $a = \frac{1}{6}; b = \frac{5}{6}$

B. $a = - \frac{1}{6}; b = - \frac{5}{6}$

C. $a = \frac{1}{6}; b = - \frac{5}{6}$

D. $a = - \frac{1}{6}; b = \frac{5}{6}$

Xem đáp án

Đáp án cần chọn là: D

Đồ thị hàm số đi qua điểm M (−1; 1) ⇒ 1 = a.(−1) + b. (1)

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 5 ⇒ 0 = a.5 + b (2)

Từ (1) và (2), ta có hệ $\{\begin{matrix} 1 = a . (- 1) + b \\ 0 = a .5 + b \end{matrix} \Leftrightarrow \{\begin{matrix} - a + b = 1 \\ 5 a + b = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} a = - \frac{1}{6} \\ b = \frac{5}{6} \end{matrix}$

Câu 2:

Cho hai đường thẳng y = 3x – 2 (d1) và y = 2mx + m – 1 (d2). Tìm giá trị m để (d1) cắt (d2) tại điểm có hoành độ bằng 2.

A. m = 1

B. m = −1

C. m = 5

D. Không tồn tại

Xem đáp án

Đáp án cần chọn là: A

Thay x = 2 vào phương trình đường thẳng (d1): y = 3.2 – 2 = 4.

Suy ra điểm A(2; 4) là giao điểm của hai đường thẳng (d1), (d2).

Điều này có nghĩa tọa độ điểm A phải thỏa mãn phương trình đường thẳng (d2).

Tức là 4 = 2m.2 + m – 1 ⇔ m = 1.

Câu 3:

Tìm giá trị thực của m để hai đường thẳng d: y = mx − 3 và

Δ: y + x = m cắt nhau tại một điểm nằm trên trục tung.

A. m = −3

B. m = 3

C. m = ±3

D. m = 0

Xem đáp án

Đáp án cần chọn là: A

Gọi A(0; a) là giao điểm hai đường thẳng nằm trên trục tung

$\Rightarrow \{\begin{matrix} A \in d \\ A \in Δ \end{matrix} \Rightarrow \{\begin{matrix} a = 0. m - 3 \\ a + 0 = m \end{matrix} \Leftrightarrow \{\begin{matrix} a = - 3 \\ m = - 3 \end{matrix}$

Câu 4:

Tìm tất cả các giá trị thực của m để hai đường thẳng d: y = mx − 3 và

Δ: y + x = m cắt nhau tại một điểm nằm trên trục hoành.

A. $m = \sqrt{3}$

B. $m = \pm \sqrt{3}$

C. $m = - \sqrt{3}$

D. $m = 3$

Xem đáp án

Đáp án cần chọn là: B

Gọi B (b; 0) là giao điểm hai đường thẳng nằm trên trục hoành

$\Rightarrow \{\begin{matrix} B \in d \\ B \in Δ \end{matrix} \Rightarrow \{\begin{matrix} 0 = m . b - 3 \\ 0 + b = m \end{matrix} \Leftrightarrow \{\begin{matrix} b^{2} = 3 \\ b = m \end{matrix} \Leftrightarrow [\begin{matrix} b = m = \sqrt{3} \\ b = m = - \sqrt{3} \end{matrix}$

Câu 5:

Tìm m để ba đường thẳng y = 2x – 3 (d1); y = x – 1 (d2); y = (m − 1)x + 2 (d3) đồng quy.

A. m = 1

B. m = −1

C. m = $- \frac{1}{2}$

D. m = $\frac{1}{2}$

Xem đáp án

Đáp án cần chọn là: D

Tọa độ giao điểm A của hai đường thẳng (d1), (d2) là nghiệm của hệ phương trình

$\{\begin{matrix} y = 2 x - 3 \\ y = x - 1 \end{matrix} \Rightarrow \{\begin{matrix} x = 2 \\ y = 1 \end{matrix} \Rightarrow A (2; 1)$

Để ba đường thẳng (d1), (d2), (d3) đồng quy thì tọa độ điểm A phải thỏa mãn phương trình đường thẳng (d3) hay A ∈ (d3).

Tức là 1 = (m − 1).2 + 2 ⇔ m = $\frac{1}{2}$ .

Câu 6:

Hàm số $y = |x + 1| + |x - 3|$ được viết lại là:

A. $y = \{\begin{matrix} - 2 x + 2 k h i x \leq - 1 \\ 4 k h i - 1 < x \leq 3 \\ 2 x - 1 k h i x > 3 \end{matrix}$

B. $y = \{\begin{matrix} 2 x - 2 k h i x \leq - 1 \\ 4 k h i - 1 < x \leq 3 \\ - 2 x + 2 k h i x > 3 \end{matrix}$

C. $y = \{\begin{matrix} 2 x + 2 k h i x \leq - 1 \\ 4 k h i - 1 < x \leq 3 \\ - 2 x - 2 k h i x > 3 \end{matrix}$

D. $y = \{\begin{matrix} - 2 x + 2 k h i x \leq - 1 \\ 4 k h i - 1 < x \leq 3 \\ 2 x - 2 k h i x > 3 \end{matrix}$

Xem đáp án

Đáp án cần chọn là: D

Ta có bảng:

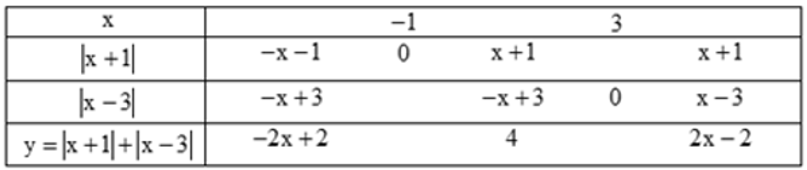
Từ bảng trên ta có kết luận: $y = \{\begin{matrix} - 2 x + 2 k h i x \leq - 1 \\ 4 k h i - 1 < x \leq 3 \\ 2 x - 2 k h i x > 3 \end{matrix}$

Câu 7:

Biết rằng đồ thị hàm số y = ax + b đi qua điểm N (4; −1) và vuông góc với đường thẳng 4x – y + 1 = 0. Tính tích P = ab.

A. $P = 0$

B. $P = - \frac{1}{4}$

C. $P = \frac{1}{4}$

D. $P = - \frac{1}{2}$

Xem đáp án

Đáp án cần chọn là: A

Đồ thị hàm số đi qua điểm N (4; −1) nên −1 = a.4 + b. (1)

Mặt khác, đồ thị hàm số vuông góc với đường thẳng y = 4x + 1 nên 4.a = −1 (2)

Từ (1) và (2), ta có hệ $\{\begin{matrix} - 1 = a .4 + b \\ 4 a = - 1 \end{matrix} \Leftrightarrow \{\begin{matrix} a = - \frac{1}{4} \\ b = 0 \end{matrix} \Rightarrow P = a b = 0$

Câu 8:

Có bao nhiêu giá trị nguyên của m thuộc đoạn [0; 3] để hàm số

y = (m²− 1)x đồng biến trên R.

A. 0

B. 1

C. 2

D. Kết quả khác

Xem đáp án

Đáp án cần chọn là: C

Để hàm số đã cho đồng biến trên R thì m²– 1 > 0 ⇔ $[\begin{matrix} m < - 1 \\ m > 1 \end{matrix}$

Kết hợp với điều kiện m ∈ [0; 3] ⇒ m ∈ (1; 3] thì có hai giá trị nguyên là

m = 2 và m = 3

Câu 9:

Biết rằng đồ thị hàm số y = ax + b đi qua điểm M (1; 4) và song song với đường thẳng y = 2x + 1. Tính tổng S = a + b.

A. S = 4

B. S = 2

C. S = 0

D. S = −4

Xem đáp án

Đáp án cần chọn là: A

Đồ thị hàm số đi qua điểm M (1; 4) nên 4 = a.1 + b (1)

Mặt khác, đồ thị hàm số song song với đường thẳng y = 2x + 1 nên $\{\begin{matrix} a = 2 \\ b \neq 1 \end{matrix}$ (2)

Từ (1) và (2), ta có hệ $\{\begin{matrix} 4 = a .1 + b \\ a = 2 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 2 \\ b = 2 \end{matrix} \Rightarrow a + b = 4$

Câu 10:

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017; 2017] để hàm số y = (m − 2)x + 2m đồng biến trên R.

A. 2014

B. 2016

C. Vô số

D. 2015

Xem đáp án

Đáp án cần chọn là: D

Hàm số bậc nhất y = ax + b đồng biến ⇔ a > 0 ⇒ m – 2 > 0 ⇔ m > 2

Mà m ∈ Z và m ∈ [−2017; 2017] ⇒ m ∈ {3; 4; 5;...; 2017}.

Vậy có 2017 – 3 + 1 = 2015 giá trị nguyên của m cần tìm

Câu 11:

Cho hàm số y = |2x − 4|. Bảng biến thiên nào sau đây là bảng biến thiên của hàm số đã cho

A. VietJack

B. VietJack

C. VietJack

D. VietJack

Xem đáp án

Đáp án cần chọn là: A

Ta có: $y = |2 x - 4| = \{\begin{matrix} 2 x - 4 k h i x \geq 2 \\ - 2 x + 4 k h i x < 2 \end{matrix}$

Hàm số $y = 2 x - 4$ luôn đồng biến và $y = - 2 x + 4$ luôn nghịch biến nên ta có:

Bảng biến thiên:

Câu 12:

Hàm số $y = \{\begin{matrix} 2 x k h i x \geq 1 \\ x + 1 k h i x < 1 \end{matrix}$ có đồ thị

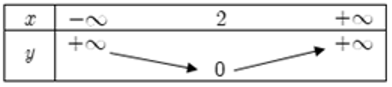
A. VietJack

B. VietJack

C. VietJack

D. VietJack

Xem đáp án

Đáp án cần chọn là: C

Ta có đồ thị hàm số $y = \{\begin{matrix} 2 x k h i x \geq 1 \\ x + 1 k h i x < 1 \end{matrix}$ như sau:

Câu 13:

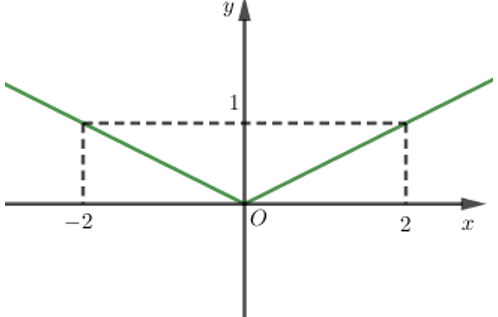
Đồ thị sau đây biểu diễn hàm số nào?

A. y = |x|

B. y = |2x|

C. $y = |\frac{1}{2} x|$

D. y = |3−x|

Xem đáp án

Đáp án cần chọn là: C

Đồ thị hàm số đi qua hai điểm A (−2; 1) và B (2; 1).

- Thay tọa độ A vào đáp án A ta được: 1 = |−2| (loại).

- Thay tọa độ A vào đáp án B ta được: 1 = |2.(−2)| (loại).

- Thay tọa độ A và B vào đáp án C ta được: $1 = |\frac{1}{2} . (- 2)|$ và $1 = |\frac{1}{2} .2|$ nên C thỏa mãn.

- Thay tọa độ A vào đáp án D ta được: 1 = |3 − (−2)| (loại).

Câu 14:

Xét ba đường thẳng sau: 2x – y + 1 = 0; x + 2y – 17 = 0; x + 2y – 3 = 0. Chọn kết luận đúng:

A. Ba đường thẳng đồng qui.

B. Ba đường thẳng giao nhau tại ba điểm phân biệt

C. Hai đường thẳng song song, đường thẳng còn lại vuông góc với hai đường thẳng song song đó.

D. Ba đường thẳng song song nhau.

Xem đáp án

Đáp án cần chọn là: C

Ta có: $2 x - y + 1 = 0 \Leftrightarrow y = 2 x + 1$

$x + 2 y - 17 = 0 \Leftrightarrow y = - \frac{1}{2} x + \frac{17}{2}$

$x + 2 y - 3 = 0 \Leftrightarrow y = - \frac{1}{2} x + \frac{3}{2}$

Dễ thấy hai đường thẳng sau có $- \frac{1}{2} = - \frac{1}{2}$ và $\frac{17}{2} \neq \frac{3}{2}$ nên chúng song song

Lại có $- \frac{1}{2} .2 = - 1$ nên đường thẳng thứ nhất vuông góc với cả hai đường thẳng sau.

Câu 15:

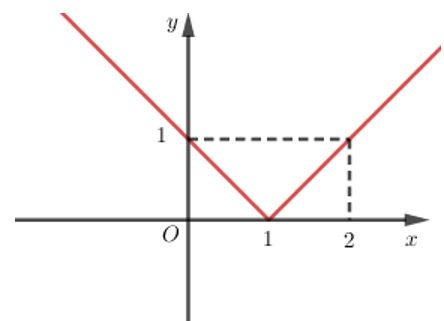
Đồ thị sau đây biểu diễn hàm số nào?

A. y = |x + 1|

B. y = |x − 1|

C. y = |x| + 1

D. y = |x| − 1

Xem đáp án

Đáp án cần chọn là: B

- Đồ thị hàm số đi qua các điểm A (0; 1), B (1; 0), C (2; 1).

- Ta thấy:

+) Tọa độ B không thỏa đáp án A vì 0 ≠ |1 + 1|, loại A.

+) Tọa độ cả ba điểm A, B, C đều thỏa B nên B thỏa mãn.

+) Tọa độ B không thỏa mãn C vì 0 ≠ |1| + 1, loại C.

+) Tọa độ A không thỏa mãn D vì 1 ≠ |0| − 1, loại D.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Hàm số y= ax + b có đáp án

Trắc nghiệm Hàm số y= ax +b có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương