10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Ôn tập chương 7 có đáp án (Vận dụng)

Câu 1:

Cho hình bình hành ABCD có A (−2; 3) và tâm I (1; 1). Biết điểm K (−1; 2) nằm trên đường thẳng AB và điểm D có hoành độ gấp đôi tung độ. Chọn kết luận đúng:

A. D (2; 1)

B. B (0; 1)

C. Cả A, B đều đúng

D. A đúng, B sai

Xem đáp án

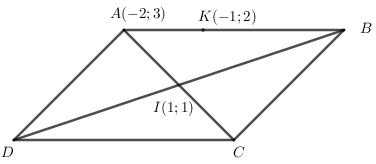
Gọi $D (2 a; a) \Rightarrow B (2 - 2 a; 2 - a)$

$\vec{A K} (1; - 1), \vec{A B} (4 - 2 a; - 1 - a)$

Vì cùng phương nên $\frac{4 - 2 a}{1} = \frac{- 1 - a}{- 1} \Rightarrow a = 1 \Rightarrow D (2; 1), B (0; 1)$

Đáp án cần chọn là: C

Câu 2:

Tìm trên trục hoành điểm P sao cho tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất biết $A (1; 2)$ và $B (3; 4)$

A. $P (\frac{5}{3}; 0)$

B. $P (- \frac{5}{3}; 0)$

C. $P (\frac{5}{2}; 0)$

D. $P (\frac{1}{3}; 0)$

Xem đáp án

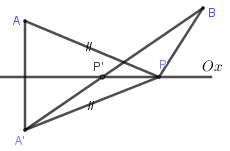
Dễ thấy A, B cùng phía với trục hoành.

Gọi A′ là điểm đối xứng với A qua trục hoành, suy ra A′ (1; −2) và PA = PA′

Ta có PA + PB = PA′ + PB ≥ A′B.

Dấu bằng xảy ra ⇔ $\vec{A' P}$ cùng phương với $\vec{A' B}$

Suy ra $\frac{x_{P} - 1}{3 - 1} = \frac{0 + 2}{4 + 2} \Rightarrow x_{P} = \frac{5}{3} \Rightarrow P (\frac{5}{3}; 0)$

Đáp án cần chọn là: A

Câu 3:

Cho tam giác ABC có A (3; 4), B (2; 1), C(−1; −2). Tìm điểm M trên đường thẳng BC sao cho $S_{A B C} = 3 S_{A B M}$

A. M (1; 0)

B. M₁(−1; 2), M₂(−3; −2)

C. M₁(1; 2), M₂(3; −2)

D. M₁(1; 0), M₂(3; 2)

Xem đáp án

Ta có $S_{A B C} = 3 S_{A B M}$ $\Leftrightarrow B C = 3 B M \Rightarrow \vec{B C} = \pm 3 \vec{B M}$

Gọi $M (x; y) \Rightarrow \vec{B M} (x - 2; y - 1); \vec{B C} (- 3; - 3)$

Suy ra $\{\begin{matrix} - 3 = 3 (x - 2) \\ - 3 = 3 (y - 1) \end{matrix} \Leftrightarrow \{\begin{matrix} x = 1 \\ y = 0 \end{matrix}$ hoặc $\{\begin{matrix} - 3 = - 3 (x - 2) \\ - 3 = - 3 (y - 1) \end{matrix} \Leftrightarrow \{\begin{matrix} x = 3 \\ y = 2 \end{matrix}$

Vậy có hai điểm thỏa mãn $M_{1} (1; 0), M_{2} (3; 2)$

Đáp án cần chọn là: D

Câu 4:

Trong mặt phẳng tọa độ Oxy, cho ba điểm A (6; 3), B (−3; 6), C (1; −2). Gọi điểm D trên trục hoành sao cho ba điểm A, B, D thẳng hàng, điểm E thuộc đoạn BC sao cho BE = 2EC. Xác định giao điểm hai đường thẳng DE và AC.

A. $I (- \frac{7}{2}; \frac{1}{2})$

B. $I (\frac{3}{2}; - \frac{1}{2})$

C. $I (\frac{7}{4}; \frac{1}{2})$

D. $I (\frac{7}{2}; \frac{1}{2})$

Xem đáp án

D trên trục hoành $\Rightarrow D (a; 0)$

Ba điểm A, B, D thẳng hàng suy ra $\vec{A B}$ và $\vec{A D}$ cùng phương

Mặt khác $\vec{A D} (a - 6; - 3)$ do đó $\frac{a - 6}{- 9} = \frac{- 3}{3} \Rightarrow a = 15$

Vậy D (15; 0)

Vì E thuộc đoạn BC và BE = 2EC suy ra $\vec{B E} = 2 \vec{E C}$

Gọi E (m; n) khi đó $\vec{B E} (m + 3; n - 6); \vec{E C} (1 - m; - 2 - n)$

Do đó $\{\begin{matrix} m + 3 = 2 (1 - m) \\ n - 6 = 2 (- 2 - n) \end{matrix} \Leftrightarrow \{\begin{matrix} m = - \frac{1}{3} \\ n = \frac{2}{3} \end{matrix}$

Vậy $E (- \frac{1}{3}; \frac{2}{3})$

Gọi I (x; y) là giao điểm của DE và AC

Do đó $\vec{D I} (x - 15; y), \vec{D E} (- \frac{46}{3}; \frac{2}{3})$ cùng phương

Suy ra $\frac{3 (x - 15)}{- 46} = \frac{3 y}{2} \Rightarrow x + 23 y - 15 = 0$ (1)

$\vec{A I} (x - 6; y - 3), \vec{A C} (- 5; - 5)$ cùng phương

Suy ra $\frac{x - 6}{- 5} = \frac{y - 3}{- 5} \Rightarrow x - y - 3 = 0$ (2)

Từ (1) và (2) suy ra $x = \frac{7}{2}, y = \frac{1}{2}$

Vậy giao điểm hai đường thẳng DE và AC là $I (\frac{7}{2}; \frac{1}{2})$

Đáp án cần chọn là: D

Câu 5:

Trong mặt phẳng tọa độ Oxy cho A (3; −1), B (−1; 2) và I (1; −1). Gọi C, D là các điểm sao cho tứ giác ABCD là hình bình hành, biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD.

A. $O (3; - \frac{7}{2})$

B. $O (2; - \frac{5}{2})$

C. $O (- 2; - \frac{5}{2})$

D. $O (2; \frac{5}{2})$

Xem đáp án

Vì I là trọng tâm tam giác ABC nên

$x_{I} = \frac{x_{A} + x_{B} + x_{C}}{3} \Rightarrow x_{C} = 3 x_{I} - x_{A} - x_{B} = 1$

$y_{I} = \frac{y_{A} + y_{B} + y_{C}}{3} \Rightarrow y_{C} = 3 y_{I} - y_{A} - y_{B} = - 4$

Suy ra C (1; -4)

Điểm O là tâm của hình bình hành ABCD suy ra O là trung điểm AC

Do đó:

$x_{O} = \frac{x_{A} + x_{B}}{2} = 2$ , $y_{O} = \frac{y_{A} + y_{B}}{2} = - \frac{5}{2}$

Vậy $O (2; - \frac{5}{2})$

Đáp án cần chọn là: B

Câu 6:

Cho hình bình hành ABCD có AD = 4 và chiều cao ứng với cạnh AD = 3, $\hat{B A D} = 60^{0}$ . Chọn hệ trục tọa độ $(A; \vec{i}; \vec{j})$ sao cho $\vec{i}$ và $\vec{A D}$ cùng hướng, y_B > 0. Tìm khẳng định sai?

A. $\vec{A B} = (\sqrt{3}; 3)$

B. $\vec{A C} = (4 + \sqrt{3}; 3)$

C. $\vec{C D} = (\sqrt{3}; - 3)$

D. $\vec{B C} = (4; 0)$

Xem đáp án

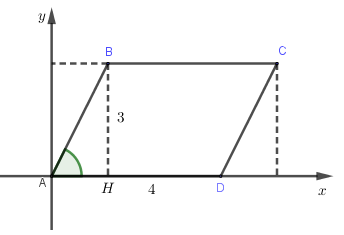
Kẻ $B H ⊥ A D \Rightarrow B H = 3; A B = \frac{B H}{\sin 60^{0}} = \frac{3}{\frac{\sqrt{3}}{2}} = 2 \sqrt{3}$

$A H = \sqrt{A B^{2} - B H^{2}} = \sqrt{12 - 9} = \sqrt{3}$

Do đó:

$A (0; 0); B (\sqrt{3}; 3); C (4 + \sqrt{3}; 3); D (4; 0)$

$\vec{A B} = (\sqrt{3}; 3)$ , $\vec{B C} = (4; 0)$ ,

$\vec{C D} = (- \sqrt{3}; - 3)$ , $\vec{A C} = (4 + \sqrt{3}; 3)$

Đáp án cần chọn là: C

Câu 7:

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB, O là điểm bất kì. Khẳng định nào sau đây là đúng nhất?

A. $\vec{O A} + \vec{O B} + \vec{O C} = \frac{\vec{O M} + \vec{O N} + \vec{O P}}{2}$

B. $\vec{O A} + \vec{O B} + \vec{O C} = \frac{\vec{O M} + \vec{O N} + \vec{O P}}{3}$

C. $\vec{O A} + \vec{O B} + \vec{O C} = \frac{\vec{O M} + \vec{O N} + \vec{O P}}{4}$

D. $\vec{O A} + \vec{O B} + \vec{O C} = \vec{O M} + \vec{O N} + \vec{O P}$

Xem đáp án

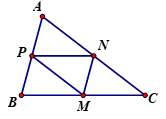
Theo quy tắc ba điểm ta có:

$\vec{O A} + \vec{O B} + \vec{O C} = (\vec{O P} + \vec{P A}) + (\vec{O M} + \vec{M B}) + (\vec{O N} + \vec{N C})$

$= (\vec{O M} + \vec{O N} + \vec{O P}) + \vec{P A} + \vec{M B} + \vec{N C}$

$= (\vec{O M} + \vec{O N} + \vec{O P}) - (\vec{B M} + \vec{C N} + \vec{A P})$

Vì PN, MN là đường trung bình của tam giác ABC nên

$P N / / B M, M N / / B P$ suy ra tứ giác BMNP là hình bình hành

$\Rightarrow \vec{B M} = \vec{P N}$

N là trung điểm của AC $\Rightarrow \vec{C N} = \vec{N A}$

Do đó theo quy tắc ba điểm ta có:

$\vec{B M} + \vec{C N} + \vec{A P} = (\vec{P N} + \vec{N A}) + \vec{A P}$

$= \vec{P A} + \vec{A P} = \vec{0}$

Do đó $\vec{O A} + \vec{O B} + \vec{O C} = \vec{O M} + \vec{O N} + \vec{O P}$

Đáp án cần chọn là: D

Câu 8:

Cho hình thoi ABCD cạnh a và $\hat{B C D} = 60^{0}$ . Gọi O là tâm hình thoi. Chọn kết luận đúng?

A. $|\vec{A B} + \vec{A D}| = a \sqrt{3}$

B. $|\vec{O B} - \vec{D C}| = \frac{a \sqrt{3}}{4}$

C. Cả A, B đều đúng

D. Cả A, B đều sai

Xem đáp án

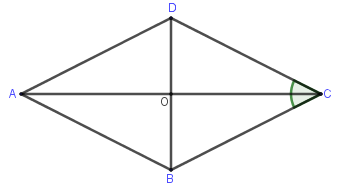
Ta có: $|\vec{A B} + \vec{A D}| = |\vec{A C}|$ (quy tắc hình bình hành)

Xét tam giác BCD có CD = CB = a và góc $\hat{B C D} = 60^{0}$ nên tam giác BCD đều cạnh a, suy ra BD = a

Xét tam giác DOC có $\hat{O} = 90^{0}$ và $D C = a, D O = \frac{1}{2} D B = \frac{a}{2}$ nên

$C O = \sqrt{D C^{2} - D O^{2}} = \sqrt{a^{2} - \frac{a^{2}}{4}} = \frac{a \sqrt{3}}{2}$

Do đó $A C = 2 O C = 2. \frac{a \sqrt{3}}{2} = a \sqrt{3}$ hay $|\vec{A B} + \vec{A D}| = a \sqrt{3}$ nên A đúng

Lại có:

$\vec{O B} - \vec{D C} = \vec{D O} - \vec{D C} = \vec{C O}$ nên $|\vec{O B} - \vec{D C}| = |\vec{C O}| = C O = \frac{a \sqrt{3}}{2}$

$|\vec{O B} - \vec{D C}| = C O = \frac{a \sqrt{3}}{2} \neq \frac{a \sqrt{3}}{4}$ nên B sai

Đáp án cần chọn là: A

Câu 9:

Cho hình vuông ABCD có tâm là O và cạnh a. M là một điểm bất kỳ. Chứng minh rằng $\vec{u} = \vec{M A} + \vec{M B} - \vec{M C} - \vec{M D}$ không phụ thuộc vị trí điểm M. Tính độ dài vectơ $\vec{u}$

A. 2a

B. 3a

C. a

D. 4a

Xem đáp án

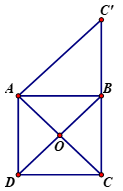
Theo quy tắc phép trừ ta có

$\vec{u} = (\vec{M A} - \vec{M C}) + (\vec{M B} - \vec{M D}) = \vec{C A} + \vec{D B}$

Suy ra $\vec{u}$ không phụ thuộc vị trí điểm M.

Qua A kẻ đường thẳng song song với DB cắt BC tại C′.

Khi đó tứ giác ADBC′ là hình bình hành (vì có cặp cạnh đối song song) suy ra

$\vec{D B} = \vec{A C'}$

Do đó $\vec{u} = \vec{C A} + \vec{A C'} = \vec{C C^{'}}$

Vì vậy $|\vec{u}| = |\vec{C C^{'}}| = B C + B C' = a + a = 2 a$

Đáp án cần chọn là: A

Theo quy tắc phép trừ ta có

Suy ra không phụ thuộc vị trí điểm M.

Qua A kẻ đường thẳng song song với DB cắt BC tại C′.

Khi đó tứ giác ADBC′ là hình bình hành (vì có cặp cạnh đối song song) suy ra

Do đó

Vì vậy

Đáp án cần chọn là: A

Câu 10:

Cho tam giác ABC vuông tại A và có $B C = a \sqrt{5}$ . Tính độ dài của vec tơ $\vec{A B} + \vec{A C}$

A. $a \sqrt{2}$

B. $a \sqrt{5}$

C. $a \sqrt{7}$

D. $a \sqrt{3}$

Xem đáp án

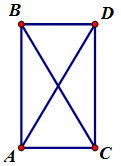
Gọi D là điểm sao cho tứ giác ABDC là hình bình hành.

Khi đó theo quy tắc hình bình hành ta có $\vec{A B} + \vec{A C} = \vec{A D}$

Vì tam giác ABC vuông ở A nên tứ giác ABDC là hình chữ nhật suy ra

AD = BC = $a \sqrt{5}$

Vậy $|\vec{A B} + \vec{A C}| = |\vec{A D}| = A D = a \sqrt{5}$

Đáp án cần chọn là: B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Ôn tập chương 7 có đáp án

Trắc nghiệm Ôn tập chương 7 có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm