Trắc nghiệm Ôn tập chương 7 có đáp án
-
2823 lượt thi
-
22 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm của AB, N là điểm đối xứng với C qua D. Độ dài vec tơ là:
 Xem đáp án
Xem đáp án
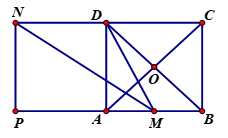
Qua N kẻ đường thẳng song song với AD cắt AB tại P.
Khi đó tứ giác ADNP là hình vuông và PM = PA + AM =
Áp dụng định lý Pitago trong tam giác vuông NPM ta có
MN2 = NP2 + PM2 =
Suy ra
Đáp án cần chọn là: A
Câu 2:
Cho tam giác ABC đều cạnh a và G là trọng tâm. Gọi I là trung điểm của AG. Tính độ dài của vectơ
 Xem đáp án
Xem đáp án
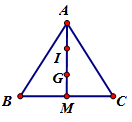
Ta có:
Gọi M là trung điểm của BC
Tam giác ABM vuông tại M nên
Ta có
Mà I là trung điểm AG nên
Đáp án cần chọn là: B
Câu 3:
Cho hình bình hành ABCD. Trên các đoạn thẳng DC, AB theo thứ tự lấy các điểm M, N sao cho DM = BN. Gọi P là giao điểm của AM, DB và Q là giao điểm của CN, DB. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
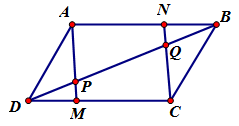
Ta có DM = BN ⇒ AN = MC, mặt khác AN song song với MC do đó tứ giác ANCM là hình bình hành
Suy ra
Xét tam giác ΔDMP và ΔBNQ ta có DM = NB (giả thiết), (so le trong)
Mặt khác (đối đỉnh) và (hai góc đồng vị) suy ra
Do đó ΔDMP = ΔBNQ (g.c.g) suy ra DP = QB.
Dễ thấy cùng hướng vì vậy .
Đáp án cần chọn là: C
Câu 4:
Cho tam giác ABC có trọng tâm G. Gọi I là trung điểm của BC. Dựng điểm B’ sao cho , gọi J là trung điểm của BB’. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
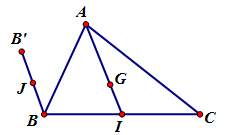
Ta có: suy ra
Dễ thấy cùng hướng (1)
Vì G là trọng tâm tam giác ABC nên , J là trung điểm BB’ suy ra
Vì vậy BJ = IG (2)
Từ (1) và (2) ta có:
Đáp án cần chọn là: B
Câu 5:
Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A (0; 3), D (2; 1) và
I (−1; 0) là tâm của hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC.
 Xem đáp án
Xem đáp án
Gọi M là tọa độ trung điểm của cạnh AD ⇒ M (1; 2)
Gọi N (xN; yN) là tọa độ trung điểm của cạnh BC.
Do I là tâm của hình chữ nhật ABCD ⇒ I là trung điểm của MN.
Suy ra
Đáp án cần chọn là: C
Câu 6:
Trong hệ tọa độ Oxy, cho ba điểm A (0; −3), B (2; 1), D (5; 5) Tìm tọa độ điểm C để tứ giác ABCD là hình bình hành.
 Xem đáp án
Xem đáp án
Gọi C (x; y). Ta có:
Tứ giác ABCD là hình bình hành
Đáp án cần chọn là: C
Câu 7:
Cho tứ giác ABCD trên cạnh AB, CD lần lượt lấy các điểm M, N sao cho
và . Tính vec tơ theo hai vec tơ
 Xem đáp án
Xem đáp án
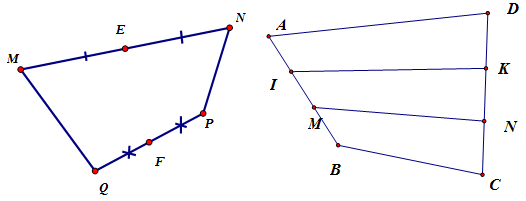
Ta chứng minh bài toán sau:
Gọi E, F lần lượt là trung điểm của MN, PQ thì ta có:
Thật vậy, ta có:
=
Gọi I, K lần lượt là trung điểm của AM và DN
Khi đó áp dụng kết quả của bài toán trên ta có:
Đáp án cần chọn là: C
Câu 8:
Cho . Gọi M, N là các điểm thỏa mãn , và . Tìm k để ba điểm M, N, P thẳng hàng
 Xem đáp án
Xem đáp án
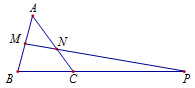
Cách 1: Tự luận
Ta có:
(1)
Để ba điểm M, N, P thẳng hàng thì
Điều kiện:
Vậy
Cách 2: Trắc nghiệm
Ta có:
Theo định lí Menelaus ba điểm M, N, P thẳng hàng khi:
Vậy
Đáp án cần chọn là: A
Câu 9:
Cho hai vec tơ và thỏa mãn các điều kiện . Đặt và , . Tìm tất cả các giá trị của k sao cho
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Câu 10:
Cho tứ giác ABCD, trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho và . Tính vec tơ theo hai vec tơ
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: C
Câu 11:
Cho tam giác ABC. Tập hợp những điểm M sao cho là:
 Xem đáp án
Xem đáp án
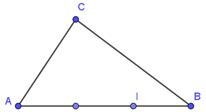
Gọi I là điểm trên cạnh AB sao cho , ta có:
=
Vậy M nằm trên đường tròn tâm I, bán kính R = 2AB với I nằm trên cạnh AB sao cho IA = 2IB.
Đáp án cần chọn là: A
Câu 12:
Cho tam giác ABC. Gọi M là điểm được xác định: . Khi đó vec tơ bằng:
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: D
Câu 13:
Tam giác ABC thỏa mãn: thì tam giác ABC là
 Xem đáp án
Xem đáp án
Gọi M là trung điểm BC
Ta có:
Trung tuyến kẻ từ A bằng một nửa cạnh BC nên tam giác ABC vuông tại A
Đáp án cần chọn là: A
Câu 14:
Trong mặt phẳng tọa độ Oxy, tọa độ điểm N trên cạnh BC của tam giác ABC có sao cho SABN = 3SANC là:
 Xem đáp án
Xem đáp án
Gọi H là chân đường cao kẻ từ A của tam giác ABC
Theo đề ta có: SABN = 3SANC
(*)
Ta có
Do đó (*) Vậy
Đáp án cần chọn là: B
Câu 15:
Cho hình thang ABCD có đáy AB = a, CD = 2a. Gọi M, N lần lượt là trung điểm AD và BC. Tính độ dài của vec tơ
 Xem đáp án
Xem đáp án
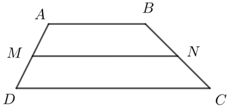
Ta có M, N là trung điểm của AD và BC nên và
Khi đó:
Đáp án cần chọn là: C
Câu 16:
Trên mặt phẳng tọa độ Oxy, cho vuông tại A có và . Tìm tọa độ điểm H là chân đường cao kẻ từ đỉnh A của , biết AB = 3, AC = 4
 Xem đáp án
Xem đáp án
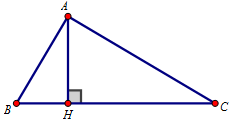
Ta có: và .
Do đó:
Mà ngược hướng nên
Khi đó, gọi thì
Suy ra:
Đáp án cần chọn là: B
Câu 17:
Cho hai lực cùng tác động vào một vật tại điểm M cường độ hai lực lần lượt là: 300 (N) và 400 (N). . Tìm cường độ của lực tổng hợp tác động vào vật.
 Xem đáp án
Xem đáp án
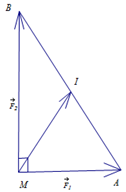
Cường độ lực tổng hợp của (I là trung điểm của AB)
Ta có: suy ra (N)
Đáp án cần chọn là: D
Câu 18:
Cho tam giác ABC, M và N là hai điểm thỏa mãn: , . Xác định x để A, M, N thẳng hàng
 Xem đáp án
Xem đáp án
Ta có:
Để A, M, N thẳng hàng thì sao cho
Hay
Đáp án cần chọn là: D
Câu 19:
Cho ΔABC. Tìm tập hợp các điểm M sao cho:
 Xem đáp án
Xem đáp án
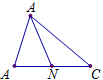
Gọi I là điểm thỏa mãn:
(1)
Gọi N là trung điểm BC. Ta được
(1)
I, A, N cố định nên tập hợp các điểm M là đường tròn tâm I, bán kính AN
Đáp án cần chọn là: A
Câu 20:
Tam giác ABC là tam giác nhọn có AA’ là đường cao
Khi đó vec tơ là:
 Xem đáp án
Xem đáp án
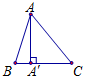
Ta thấy hai vec tơ và ngược hướng và độ dài mỗi vec tơ bằng AA’ nên chúng là hai vec tơ đối nhau
Vậy
Đáp án cần chọn là: B
Câu 21:
Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Biết M (1; 1), N (−2; −3), P (2; −1). Chọn đáp án đúng nhất:
 Xem đáp án
Xem đáp án
Ta có:
N là trung điểm AC suy ra
Tương tự M là trung điểm BC suy ra B (5; 3)
Đáp án cần chọn là: B
