15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Tích vô hướng của hai vecto và ứng dụng có đáp án

Câu 1:

Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số $\frac{R}{r}$ bằng:

$A . 1 + \sqrt{2}$

$B . \frac{2 + \sqrt{2}}{2}$

$C . \frac{\sqrt{2} - 1}{2}$

$D . \frac{\sqrt{2} + 1}{2}$

Xem đáp án

Ta có: $R = \frac{a b c}{4 S}, r = \frac{S}{p}$

Vì tam giác ABC vuông cân tại A nên b = c và $a = \sqrt{b^{2} + c^{2}} = b \sqrt{2}$

Xét tỉ số:

$\frac{R}{r} = \frac{a b c . p}{4 S^{2}} = \frac{a b c . \frac{a + b + c}{2}}{4. \frac{1}{4} . {(b . c)}^{2}} = \frac{a (a + 2 b)}{2 b^{2}} = \frac{2 b^{2} (1 + \sqrt{2})}{2 b^{2}} = 1 + \sqrt{2}$

Đáp án cần chọn là: A

Câu 2:

Cho tam giác đều ABC cạnh 18cm. Tập hợp các điểm M thỏa mãn đẳng thức $|2 \vec{M A} + 3 \vec{M B} + 4 \vec{M C}| = |\vec{M A} - \vec{M B}|$ là:

A.Tập rỗng

B. Đường tròn cố định có bán kính R = 2cm.

C. Đường tròn cố định có bán kính R = 3cm.

D. Một đường thẳng.

Xem đáp án

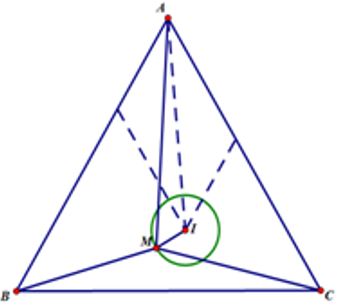
Ta có: $|\vec{M A} - \vec{M B}| = |\vec{A B}| = 18$

Dựng điểm I thỏa mãn:

$2 \vec{I A} + 3 \vec{I B} + 4 \vec{I C} = \vec{0} \Leftrightarrow \vec{A I} = \frac{1}{3} \vec{A B} + \frac{4}{9} \vec{A C}$

Khi đó: $|2 \vec{M A} + 3 \vec{M B} + 4 \vec{M C}| = |\vec{M A} - \vec{M B}|$

$\Leftrightarrow 9 |\vec{M I}| = 18 \Leftrightarrow I M = 2$

Do đó tập hợp các điểm M là đường tròn cố định có bán kính R = 2cm

Đáp án cần chọn là: B

Câu 3:

Cho hình vuông ABCD cạnh a, tâm O. Gọi M là điểm tùy ý trên đường tròn nội tiếp hình vuông. Tính $\vec{M A} . \vec{M B} + \vec{M C} . \vec{M D}$

$A . \frac{a^{2}}{2}$

$B . \frac{a^{2}}{4}$

$C . \frac{a^{2}}{8}$

$D . 0$

Xem đáp án

$\vec{M A} . \vec{M B} + \vec{M C} . \vec{M D} = (\vec{M O} + \vec{O A}) (\vec{M O} + \vec{O B}) + (\vec{M O} + \vec{O C}) (\vec{M O} + \vec{O D})$

$= 2 M O^{2} + \vec{O A} . \vec{O B} + \vec{O C} . \vec{O D} + \vec{M O} (\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D})$

Có $\vec{O A} + \vec{O C} = \vec{0}; \vec{O B} + \vec{O D} = \vec{0} \Rightarrow \vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$

$\vec{O A} ⊥ \vec{O B} \Rightarrow \vec{O A} . \vec{O B} = 0, \vec{O C} ⊥ \vec{O D} \Rightarrow \vec{O C} . \vec{O D} = 0$

Đường tròn nội tiếp hình vuông cạnh a có bán kính $\frac{a}{2} \Rightarrow M O = \frac{a}{2} \Rightarrow M O^{2} = \frac{a^{2}}{4}$

Vậy = $\vec{M A} . \vec{M B} + \vec{M C} . \vec{M D} = 2. \frac{a^{2}}{4} = \frac{a^{2}}{2}$

Đáp án cần chọn là: A

Câu 4:

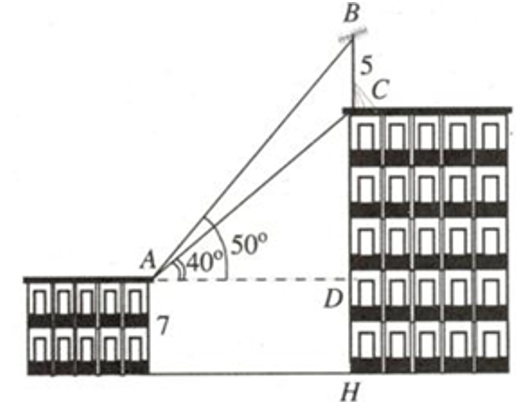
Trên nóc một tòa nhà có cột ăng-ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50⁰ và 40⁰ so với phương nằm ngang (như hình vẽ bên). Chiều cao của tòa nhà (được làm tròn đến hàng phần mười) là:

A. 21,2m

B. 14,2m

C. 11,9m

D. 18,9m

Xem đáp án

Ta có chiều cao của tòa nhà chính là đoạn HC.

Mà HC = CD + DH = CD + 7

Xét tam giác ACD vuông tại D có

$A C = \frac{C D}{\sin 40^{0}}$

Xét tam giác ABD vuông tại D có

$A B = \frac{5 + C D}{\sin 50^{0}}$

Xét tam giác ABC có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C . \cos \hat{B A C}$

$\Leftrightarrow (\frac{1}{\sin^{2} 50^{0}} + \frac{1}{\sin^{2} 40^{0}} - \frac{2 \cos 10^{0}}{\sin 40^{0} \sin 50^{0}}) C D^{2} + (\frac{10}{\sin^{2} 50^{0}} - \frac{10 \cos 10^{0}}{\sin 40^{0} \sin 50^{0}})$

$+ \frac{25}{\sin^{2} 50^{0}} - 25 = 0$

$\Leftrightarrow C D \approx 11, 9 \Rightarrow H C \approx 7 + 11, 9 \approx 18, 9 (m)$

Vậy tòa nhà cao 18,9m

Đáp án cần chọn là: D

Câu 5:

Cho tam giác ABC có a = 5 cm, c = 9 cm, $\cos C = - \frac{1}{10}$ . Tính độ dài đường cao h_a hạ từ A của tam giác ABC

$A . h_{a} = \frac{\sqrt{462}}{40} c m$

$B . h_{a} = \frac{\sqrt{462}}{100} c m$

$C . h_{a} = \frac{21 \sqrt{11}}{40} c m$

$D . h_{a} = \frac{21 \sqrt{11}}{10} c m$

Xem đáp án

Áp dụng định lí cosin trong tam giác ABC, ta có:

$c^{2} = a^{2} + b^{2} - 2 a . b . \cos C \Rightarrow 81 = 25 + b^{2} - 2.5. b . (- \frac{1}{10})$

$\Leftrightarrow b^{2} + b - 56 = 0$

$\Leftrightarrow [\begin{matrix} b = 7 \\ b = - 8 \end{matrix}$

Ta nhận được b = 7 (cm)

Diện tích tam giác ABC là $S_{Δ A B C} = \sqrt{p (p - a) (p - b) (p - c)}$

$= \sqrt{\frac{21}{2} (\frac{21}{2} - 5) (\frac{21}{2} - 7) (\frac{21}{2} - 9)} = \frac{21 \sqrt{11}}{4} (c m^{2})$

Độ dài đường cao $h_{a} = \frac{2 S}{a} = \frac{\frac{21 \sqrt{11}}{2}}{5} = \frac{21 \sqrt{11}}{10} (c m)$

Đáp án cần chọn là: D

Câu 6:

Cho đường tròn tâm O bán kính R và điểm M thỏa mãn MO = 3R. Một

đường kính AB thay đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức

S = MA + MB.

A. Min S=6R

B. Min S=4R

C. Min S=2R

D. Min S=R

Xem đáp án

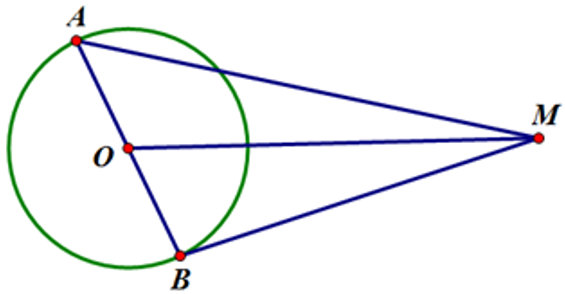
Gọi $\hat{M O A} = α \Rightarrow \hat{M O B} = 180^{0} - α$

Ta có: $M A = \sqrt{M O^{2} + A O^{2} - 2 M O . A O . \cos α}$

$= \sqrt{9 R^{2} + R^{2} - 6 R^{2} \cos α} = R \sqrt{10 - 6 \cos α}$

$M B = \sqrt{M O^{2} + B O^{2} - 2 M O . B O . \cos (180^{0} - α)}$

$= \sqrt{9 R^{2} + R^{2} + 6 R^{2} \cos α} = R \sqrt{10 + 6 \cos α}$

Xét $C = \sqrt{10 - 6 \cos α} + \sqrt{10 + 6 \cos α}$

$\Rightarrow C^{2} = 20 + 2 \sqrt{100 - 36 \cos^{2} α} \geq 20 + 2 \sqrt{100 - 36} = 36$

Suy ra $C \geq 6$ . Dấu bằng xảy ra khi $\cos^{2} α = 1 \Leftrightarrow [\begin{matrix} \cos α = 1 \\ \cos α = - 1 \end{matrix} \Leftrightarrow [\begin{matrix} α = 0^{0} \\ α = 180^{0} \end{matrix}$

Ta có $S = M A + M B = R (\sqrt{10 - 6 \cos α} + \sqrt{10 + 6 \cos α}) \geq 6 R$

Suy ra min S = 6R khi và chỉ khi A, O, B, M thẳng hàng

Đáp án cần chọn là: A

Câu 7:

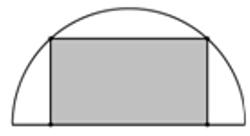
Từ một miếng tôn có hình dạng là nửa đường tròn bán kính 1m, người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu?

$A . 1, 6 m^{2} .$

B. 2m².

C. 1m².

D. 0,8m²

Xem đáp án

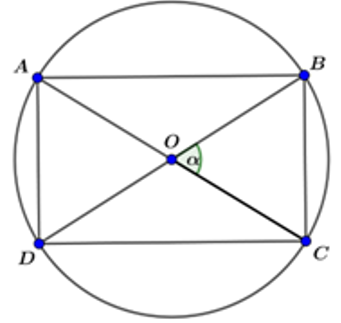
Xét đường tròn bán kính 1, ta cắt trên đó một hình chữ nhật ABCD.

Khi đó $S_{A B C D} = \frac{1}{2} A C . B D . \sin α = 2 \sin α \leq 2$

Dấu bằng xảy ra khi và chỉ khi α = 90⁰.

Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng 1.

Đáp án cần chọn là: C

Câu 8:

Cho $\vec{u} = \vec{a} + 3 \vec{b}$ vuông góc với $\vec{v} = 7 \vec{a} - 5 \vec{b}$ và $\vec{x} = \vec{a} - 4 \vec{b}$ vuông góc với $\vec{y} = 7 \vec{a} - 2 \vec{b}$ . Khi đó góc giữa hai vec tơ $\vec{a}$ và $\vec{b}$ bằng:

$A . (\vec{a}, \vec{b}) = 75^{0}$

$B . (\vec{a}, \vec{b}) = 60^{0}$

$C . (\vec{a}, \vec{b}) = 120^{0}$

$D . (\vec{a}, \vec{b}) = 45^{0}$

Xem đáp án

Ta có: $\{\begin{matrix} \vec{u} . \vec{v} = 0 \\ \vec{x} . \vec{y} = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} (\vec{a} + 3 \vec{b}) . (7 \vec{a} - 5 \vec{b}) = 0 \\ (\vec{a} - 4 \vec{b}) . (7 \vec{a} - 2 \vec{b}) = 0 \end{matrix}$

$\Leftrightarrow \{\begin{matrix} 7 {|\vec{a}|}^{2} - 15 {|\vec{b}|}^{2} = - 16 \vec{a} . \vec{b} \\ 7 {|\vec{a}|}^{2} + 8 {|\vec{b}|}^{2} = 30 \vec{a} . \vec{b} \end{matrix}$

$\Leftrightarrow \{\begin{matrix} {|\vec{b}|}^{2} = 2 \vec{a} . \vec{b} \\ {|\vec{a}|}^{2} = 2 \vec{a} . \vec{b} \end{matrix} \Leftrightarrow \Leftrightarrow \{\begin{matrix} {|\vec{b}|}^{2} = 2 \vec{a} . \vec{b} \\ |\vec{a}| = |\vec{b}| \end{matrix}$

Từ đó, ta có: $\cos (\vec{a} . \vec{b}) = \frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|} = \frac{\vec{a} . \vec{b}}{{|\vec{b}|}^{2}} = \frac{1}{2}$

$\Rightarrow (\vec{a}, \vec{b}) = 60^{0}$

Đáp án cần chọn là: B

Câu 9:

Cho tam giác ABC vuông tại A, $B C = a \sqrt{3}$ , M là trung điểm của BC và có $\vec{A M} . \vec{B C} = \frac{a^{2}}{2}$ . Tính cạnh AB, AC

$A . A B = a, A C = a \sqrt{2}$

$B . A B = a \sqrt{2}, A C = a \sqrt{2}$

$C . A B = a \sqrt{2}, A C = a$

$D . A B = a, A C = a$

Xem đáp án

$\vec{A M} . \vec{B C} = \frac{a^{2}}{2} \Rightarrow \frac{1}{2} (\vec{A B} + \vec{A C}) (\vec{A C} + \vec{A B}) = \frac{a^{2}}{2}$

$\Rightarrow A C^{2} - A B^{2} = a^{2}$

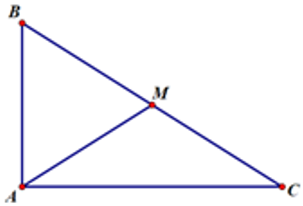
Mặt khác, tam giác ABC vuông tại A nên $A B^{2} + A C^{2} = 3 a^{2}$

Suy ra $\{\begin{matrix} A C^{2} = 2 a^{2} \\ A B^{2} = a^{2} \end{matrix} \Rightarrow \{\begin{matrix} A C = a \sqrt{2} \\ A B = a \end{matrix}$

Đáp án cần chọn là: A

Câu 10:

Đoạn thẳng AB có độ dài 2a, I là trung điểm AB. Khi $\vec{M A} . \vec{M B} = 3 a^{2}$ . Độ dài MI là:

A. 2a

B. a

$C . a \sqrt{3}$

$D . a \sqrt{7}$

Xem đáp án

Đáp án cần chọn là: A

Câu 11:

Cho tam giác ABC đều cạnh bằng a. Tập hợp các điểm M thỏa mãn đẳng thức $4 M A^{2} + M B^{2} + M C^{2} = \frac{5 a^{2}}{2}$ nằm trên một đường tròn có bán kính R. Tính R?

$A . R = \frac{a}{\sqrt{3}}$

$B . R = \frac{a}{4}$

$C . R = \frac{a \sqrt{3}}{2}$

$D . R = \frac{a}{\sqrt{6}}$

Xem đáp án

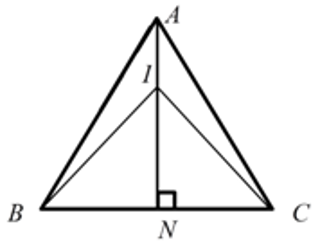
Gọi N là trung điểm đoạn BC

Gọi I là điểm thỏa: $4 \vec{I A} + \vec{I B} + \vec{I C} = \vec{0} \Leftrightarrow 4 \vec{I A} + 2 \vec{I N} = \vec{0}$

$\Leftrightarrow 2 \vec{I A} + \vec{I N} = \vec{0}$ nên điểm I thuộc đoạn thẳng AN sao cho IN = 2IA

Khi đó: $I A = \frac{1}{3} A N = \frac{1}{3} \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{6}$ và $I N = \frac{2}{3} A N = \frac{2}{3} . \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{3}$

$I B^{2} = I C^{2} = I N^{2} + B N^{2} = \frac{a^{2}}{3} + \frac{a^{2}}{4} = \frac{7 a^{2}}{12}$

Ta có: $4 M A^{2} + M B^{2} + M C^{2} = \frac{5 a^{2}}{2}$

$\Leftrightarrow 4 {(\vec{M I} + \vec{I A})}^{2} + {(\vec{M I} + \vec{I B})}^{2} + {(\vec{M I} + \vec{I C})}^{2} = \frac{5 a^{2}}{2}$

$\Leftrightarrow 6 M I^{2} + 4 I A^{2} + I B^{2} + I C^{2} = \frac{a \sqrt{5}}{2}$

$\Leftrightarrow 6 M I^{2} + 4. \frac{a^{2}}{12} + 2. \frac{7 a^{2}}{12} = \frac{5 a^{2}}{2}$

$\Leftrightarrow M I = \frac{a}{\sqrt{6}}$

Đáp án cần chọn là: D

Câu 12:

Biết $\sin α = \frac{\sqrt{2017} + 1}{2018}$ , $90^{0} < α < 180^{0}$ . Tính giá trị của biểu thức $M = \cot α + \frac{\sin α}{1 + \cos α}$

$A . M = - \frac{\sqrt{2017} + 1}{2018}$

$B . M = \frac{\sqrt{2017} + 1}{2018}$

$C . M = - \frac{2018}{\sqrt{2017} + 1}$

$D . M = \frac{2018}{\sqrt{2017} + 1}$

Xem đáp án

$M = \cot α + \frac{\sin α}{1 + \cos α} = \frac{\cos α}{\sin α} + \frac{\sin α}{1 + \cos α} = \frac{1 + \cos α}{\sin α (1 + \cos α)} = \frac{1}{\sin α}$

= $\frac{2018}{\sqrt{2017} + 1}$

Đáp án cần chọn là: D

Câu 13:

Trong hệ trục tọa độ Oxy, cho tam giác ABC có A (1; 3), B (−1; −1),

C (1; 1). Đường tròn ngoại tiếp tam giác ABC có tâm I (a; b). Giá trị a + b bằng

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Ta có: $\vec{I A} = (a - 1; b - 3) \Rightarrow I A^{2} = a^{2} + b^{2} - 2 a - 6 b + 10$

$\vec{I B} = (a + 1; b + 1) \Rightarrow I B^{2} = a^{2} + b^{2} + 2 a + 2 b + 2$

$\vec{I C} = (a - 1; b - 1) \Rightarrow I C^{2} = a^{2} + b^{2} - 2 a - 2 b + 2$

Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên:

$\Leftrightarrow \{\begin{matrix} I A = I B \\ I C = I B \end{matrix} \Leftrightarrow \{\begin{matrix} I A^{2} = I B^{2} \\ I C^{2} = I B^{2} \end{matrix} \Leftrightarrow \{\begin{matrix} a + 2 b = 2 \\ a + b = 0 \end{matrix} \Rightarrow \{\begin{matrix} a = - 2 \\ b = 2 \end{matrix}$

Vậy a + b = 0

Đáp án cần chọn là: B

Câu 14:

Cho hình thang cân ABCD có đáy nhỏ AB, đáy lớn CD. Biết AB = AD và $\tan \hat{B D C} = \frac{3}{4}$ . Tính $\cos \hat{B A D}$

$A . \frac{17}{25}$

$C . - \frac{7}{25}$

$C . \frac{5}{25}$

$D . - \frac{17}{25}$

Xem đáp án

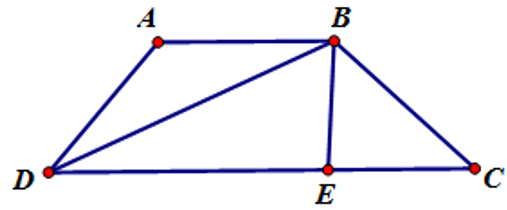
Gọi E là hình chiếu vuông góc của B trên DC. Đặt AB=AD=BC=x

Ta có: $E C = \frac{D C - x}{2}$ (1)

Trong tam giác vuông BDE ta có: $\tan \hat{B D C} = \frac{3}{4} \Leftrightarrow \frac{B E}{E D} = \frac{3}{4} \Leftrightarrow B E = \frac{3}{4} E D$

$\Leftrightarrow B E = \frac{3}{4} (D C - \frac{D C - x}{2}) = \frac{3}{8} (D C + x)$ (2)

Trong tam giác vuông BEC ta có: $B C^{2} = E C^{2} + B E^{2}$ (3)

Thay (1), (2) vào (3) biến đổi ta được:

$39 x^{2} + 14 D C . x - 25 D C^{2} = 0$

$\Leftrightarrow x = \frac{25}{39} D C h a y D C = \frac{39}{25} x$

Khi đó, $E C = \frac{7}{25} x$

Mặt khác: $\cos \hat{B A D} = - \cos \hat{B C E} = - \frac{E C}{B C} = - \frac{7}{25}$

Đáp án cần chọn là: B

Câu 15:

Cho ba vec tơ $\vec{a}, \vec{b}, \vec{c}$ thỏa mãn: $|\vec{a}| = 4; |\vec{b}| = 1; |\vec{c}| = 5$ và $5 (\vec{b} - \vec{a}) + 3 \vec{c} = \vec{0}$ . Khi đó biểu thức $M = \vec{a} . \vec{b} + \vec{b} . \vec{c} + \vec{c} . \vec{a}$ có giá trị là:

A. 29

$B . \frac{67}{2}$

$C . 18, 25$

$D . - 18, 25$

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Tích vô hướng của hai vecto và ứng dụng có đáp án

Trắc nghiệm Tích vô hướng của hai vecto và ứng dụng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương