10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Tích vô hướng của hai vecto và ứng dụng có đáp án (Vận dụng)

Câu 1:

Cho tam giác ABC biết $A (- 1; 2), B (2; 0), C (- 3; 1)$ . Tìm tọa độ điểm M thuộc BC sao cho $S_{A B M} = \frac{1}{3} S_{A B C}$

$A . M (3; \frac{1}{3})$

$B . M (- \frac{1}{3}; - \frac{1}{3})$

$C . M (1; 1)$

$D . M (\frac{1}{3}; \frac{1}{3})$

Xem đáp án

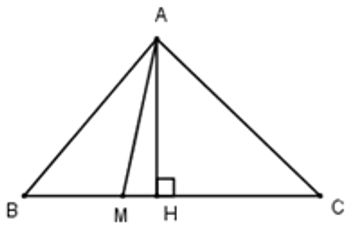
Giả sử M(x; y) là điểm thỏa mãn điều kiện đề bài.

Kẻ AH vuông góc với BC. Suy ra

$\frac{1}{2} B M . A H = \frac{1}{3} . \frac{1}{2} A H . B C \Rightarrow \vec{B M} = \frac{1}{3} \vec{B C}$

$(x - 2; y) = \frac{1}{3} (- 5; 1) \Leftrightarrow \{\begin{matrix} x - 2 = - \frac{5}{3} \\ y = \frac{1}{3} \end{matrix} \Leftrightarrow \{\begin{matrix} x = \frac{1}{3} \\ y = \frac{1}{3} \end{matrix}$

$\Rightarrow M (\frac{1}{3}; \frac{1}{3})$

Đáp án cần chọn là: D

Câu 2:

Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60⁰. Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

$A . 20 \sqrt{13}$

$B . 15 \sqrt{13}$

$C . 10 \sqrt{13}$

$D . 15$

Xem đáp án

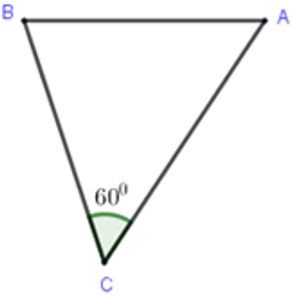
Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: S₁= 30.2 = 60km.

Sau 2h quãng đường tàu thứ hai chạy được là: S₂= 40.2 = 80km.

Vậy: sau 2h hai tàu cách nhau là: $S = \sqrt{S_{1}^{2} + S_{2}^{2} - 2 S_{1} . S_{2} . \cos 60^{0}} = 20 \sqrt{13}$

Đáp án cần chọn là: A

Câu 3:

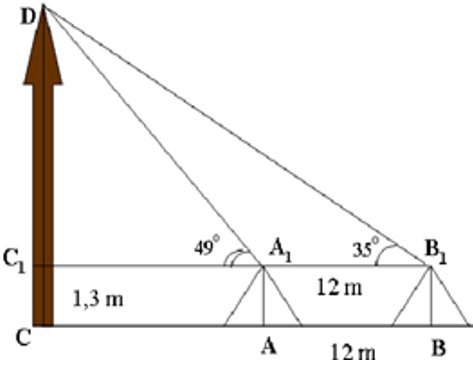
Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12m cùng thẳng hàng với chân C của tháp để đặt hai giác kế. Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm A₁, B₁ cùng thẳng hàng với C₁ thuộc chiều cao CD của tháp. Người ta đo được góc $\hat{D A_{1} C_{1}} = 49^{0}$ và $\hat{D B_{1} C_{1}} = 35^{0}$ . Tính chiều cao CD của tháp.

A. 22,77m

B. 21,47m

C. 20,47m

D. 21,77m

Xem đáp án

Ta có: $\hat{C_{1} D A_{1}} = 90^{0} - 49^{0} = 41^{0}; \hat{C_{1} D B_{1}} = 90^{0} - 35^{0} = 55^{0}$ nên $\hat{A_{1} D B_{1}} = 14^{0}$

Xét tam giác A₁DB₁ có $\frac{A_{1} B_{1}}{\sin \hat{A_{1} D B_{1}}} = \frac{A_{1} D}{\sin \hat{A_{1} B_{1} D}} \Rightarrow A_{1} D = \frac{12. \sin 35^{0}}{\sin 14^{0}}$

$\approx 28, 45 m$

Xét tam giác C₁A₁D vuông tại C₁, có:

$\sin \hat{C_{1} A_{1} D} = \frac{C_{1} D}{A_{1} D} \Rightarrow C_{1} D = A_{1} D . \sin \hat{C_{1} A_{1} D} = 28, 45. \sin 49^{0} \approx 21, 47 m$

$\Rightarrow C D = C_{1} D + C C_{1} \approx 22, 77 m$

Đáp án cần chọn là: A

Câu 4:

Cho tam giác ABC với tọa độ các đỉnh A (1; −3), B (3; −5), C (2; −2). Tìm tọa độ giao điểm E của BC với phân giác trong của góc A.

A. E (−7; 3)

B. E (7; 3)

C. E (1; 1)

D. E ( $\frac{7}{3}$ ; −3)

Xem đáp án

Ta có: $A B^{2} = 8, A C^{2} = 2 \Rightarrow \frac{A C}{A B} = \frac{1}{2}$

Giả sử E (x; y) thuộc đoạn BC. Theo tính chất đường phân giác ta có:

$\frac{E B}{A B} = \frac{E C}{A C} \Rightarrow \frac{E C}{E B} = \frac{A C}{A B} = \frac{1}{2}$

$\Rightarrow \frac{\vec{E C}}{\vec{E B}} = - \frac{1}{2}$

$\Leftrightarrow (2 - x; - 2 - y) = - \frac{1}{2} (3 - x; - 5 - y)$

$\Leftrightarrow \{\begin{matrix} 2 - x = - \frac{3}{2} + \frac{1}{2} x \\ - 2 - y = \frac{5}{2} + \frac{1}{2} y \end{matrix} \Leftrightarrow \{\begin{matrix} x = \frac{7}{3} \\ y = - 3 \end{matrix}$

$\Rightarrow E (\frac{7}{3}; - 3)$

Đáp án cần chọn là: D

Câu 5:

Cho tam giác ABC vuông cân tại A. Tính cos góc giữa hai trung tuyến BE và CF

$A . \cos a = \frac{1}{5}$

$B . \cos a = \frac{2}{5}$

$C . \cos a = \frac{4}{5}$

D. Kết quả khác

Xem đáp án

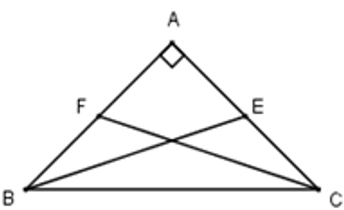
Gọi a là góc tạo bởi hai trung tuyến BE, CF

Khi đó $\cos a = \frac{|\vec{B E} . \vec{C F}|}{|\vec{B E}| |\vec{C F}|}$

Sử dụng phân tích

$\vec{B E} . \vec{C F} = (\vec{B A} + \vec{A E}) (\vec{C A} + \vec{A F})$

$= \vec{B A} . \vec{C A} + \vec{B A} . \vec{A F} + \vec{A E} . \vec{C A} + \vec{A E} . \vec{A F}$

$= 0 - \vec{A B} . \frac{\vec{A B}}{2} - \vec{A C} . \frac{\vec{A C}}{2} + 0$

$= - \frac{A B^{2}}{2} - \frac{A C^{2}}{2} = - \frac{A B^{2}}{2} - \frac{A B^{2}}{2} = - A B^{2}$

BE = CF $= \sqrt{A B^{2} + A E^{2}} = \sqrt{A B^{2} + \frac{A B^{2}}{4}} = A B \sqrt{\frac{5}{4}}$

Từ đó suy ra $\cos a = \frac{A B^{2}}{A B^{2} \frac{5}{4}} = \frac{4}{5}$

Đáp án cần chọn là: C

Câu 6:

Xác định dạng của tam giác ABC biết rằng $S = \frac{\sqrt{3}}{36} {(a + b + c)}^{2}$

A. Tam giác tù

B. Tam giác vuông

C. Tam giác đều

D. Chưa đủ điều kiện để kết luận

Xem đáp án

Với p là nửa chu vi của tam giác ta có:

$S = \frac{\sqrt{3}}{36} {(a + b + c)}^{2} = \frac{\sqrt{3}}{36} . {(2 p)}^{2} = \frac{\sqrt{3}}{9} p^{2}$

Theo công thức He-rong ta có:

$\sqrt{p (p - a) (p - b) (p - c)} = \frac{\sqrt{3}}{9} p^{2}$

$\Leftrightarrow (p - a) (p - b) (p - c) = \frac{1}{27} p^{3}$

Theo bất đẳng thức Cauchy ta có:

$(p - a) (p - b) (p - c)$

$\leq \frac{{(p - a + p - b + p - c)}^{3}}{27} = \frac{{(3 p - (a + b + c))}^{3}}{27}$

$= \frac{{(3 p - 2 p)}^{3}}{27} = \frac{p^{3}}{27}$

Đẳng thức xảy ra khi a = b = c

Khi đó tam giác ABC đều

Đáp án cần chọn là: C

Câu 7:

Tìm bán kính đường tròn ngoại tiếp tam giác ABC biết b = 7cm, c = 5cm, $\cos A = \frac{3}{5}$

$A . R = \frac{5 \sqrt{2}}{2}$

$B . R = \frac{5}{2}$

$C . R = \frac{\sqrt{2}}{2}$

$D . R = \frac{2 \sqrt{2}}{5}$

Xem đáp án

Theo định lí cosin ta có:

$a^{2} = b^{2} + c^{2} - 2 b c \cos A = 7^{2} + 5^{2} - 2.7.5. \frac{3}{5} = 32$

$\Rightarrow a = 4 \sqrt{2}$

Từ công thức $\sin^{2} A + \cos^{2} A = 1 \Rightarrow \sin A = \frac{4}{5}$

Theo định lí sin ta có: $\frac{a}{\sin A} = 2 R \Rightarrow R = \frac{a}{2 \sin A} = \frac{4 \sqrt{2}}{2. \frac{4}{5}} = \frac{5 \sqrt{2}}{2}$

Đáp án cần chọn là: A

Câu 8:

Xác định hình dạng tam giác ABC biết $\{\begin{matrix} \frac{b^{3} + c^{3} - a^{3}}{b + c - a} = a^{2} \\ a = 2 b \cos C \end{matrix}$

A. Tam giác tù

B. Tam giác vuông

C. Tam giác đều

D. Chưa đủ điều kiện để kết luận

Xem đáp án

Theo định lí cosin ta có: $\cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b}$ thay vào đẳng thức thứ hai của hệ trên. Ta có:

$a = 2 b \cos C = 2 b . \frac{a^{2} + b^{2} - c^{2}}{2 a b}$

$\Rightarrow a^{2} = a^{2} + b^{2} - c^{2} \Leftrightarrow b^{2} - c^{2} = 0$

$\Leftrightarrow b^{2} = c^{2} \Leftrightarrow b = c$

Thay b = c vào hệ thức thứ nhất ta có:

$\frac{2 b^{3} - a^{3}}{2 b - a} = a^{2} \Leftrightarrow 2 b^{3} - a^{3} = 2 b a^{2} - a^{3}$

$\Leftrightarrow b^{2} = a^{2} \Leftrightarrow a = b$

Do đó a = b = c. Vậy tam giác ABC đều

Đáp án cần chọn là: C

Câu 9:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có $A (3; 4), B (2; 1), C (- 1; - 2)$ . Gọi M (x; y) là điểm trên đường thẳng BC sao cho $S_{Δ A B C} = 4 S_{Δ A B M}$ . Tính P = x.y

$A . [\begin{matrix} P = \frac{5}{16} \\ P = \frac{7}{16} \end{matrix}$

$B . [\begin{matrix} P = \frac{77}{16} \\ P = \frac{7}{16} \end{matrix}$

$C . [\begin{matrix} P = \frac{5}{16} \\ P = \frac{77}{16} \end{matrix}$

D. Đáp án khác

Xem đáp án

Dễ thấy $\frac{S_{Δ A B C}}{S_{Δ A B M}} = 4 \Leftrightarrow \frac{B C}{B M} = 4 \Leftrightarrow [\begin{matrix} \vec{B C} = 4 \vec{B M} \\ \vec{B C} = - 4 \vec{B M} \end{matrix}$

TH1: $\vec{B C} = 4 \vec{B M} \Rightarrow \vec{B M} = \frac{1}{4} \vec{B C}$ thì $\{\begin{matrix} x - 2 = - \frac{3}{4} \\ y - 1 = - \frac{3}{4} \end{matrix} \Leftrightarrow \{\begin{matrix} x = \frac{5}{4} \\ y = \frac{1}{4} \end{matrix} \Rightarrow x . y = \frac{5}{16}$

TH2: $\vec{B C} = - 4 \vec{B M} \Rightarrow \vec{B M} = - \frac{1}{4} \vec{B C}$ thì $\{\begin{matrix} x - 2 = \frac{3}{4} \\ y - 1 = \frac{3}{4} \end{matrix} \Leftrightarrow \{\begin{matrix} x = \frac{11}{4} \\ y = \frac{7}{4} \end{matrix} \Rightarrow x . y = \frac{77}{16}$

Đáp án cần chọn là: C

Câu 10:

Cho hình vuông ABCD có cạnh bằng 1. Hai điểm M, N thay đổi lần lượt ở trên cạnh AB, AD sao cho AM = x ( $0 \leq x \leq 1$ ), DN = y ( $0 \leq y \leq 1$ ). Tìm mối liên hệ giữa x và y sao cho $C M ⊥ B N$

$A . x - y = 0$

$B . x - y \sqrt{2} = 0$

$C . x + y = 1$

$D . x - y \sqrt{3} = 0$

Xem đáp án

Chọn hệ trục tọa độ Oxy như hình vẽ.

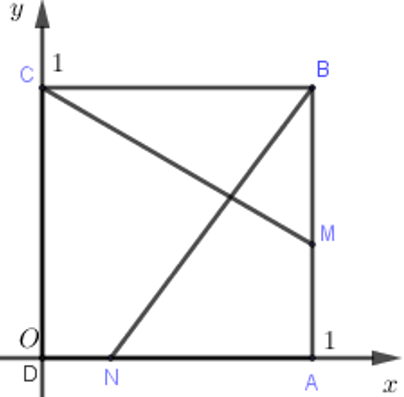
Khi đó: D (0; 0), C (0; 1), A (1; 0); B (1; 1), M (1; x); N (y; 0).

Ta có: $\vec{C M} = (1; x - 1); \vec{B N} = (y - 1; - 1)$

Do đó: $C M ⊥ B N \Leftrightarrow \vec{C M} . \vec{B N} = 0 \Leftrightarrow x - y = 0$

Đáp án cần chọn là: A

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Tích vô hướng của hai vecto và ứng dụng có đáp án

Trắc nghiệm Tích vô hướng của hai vecto và ứng dụng có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương