Dạng 2: Chứng minh các đẳng thức, hệ thức liên quan có đáp án
-
802 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tam giác ABC có BC = a, CA = b, AB = c.
Chứng minh rằng: a = b.cos C + c.cos B.
Xem đáp án
Hướng dẫn giải:
Theo định lý cô sin ta có \[{b^2} = {a^2} + {c^2} - 2ac.\cos B\].
\( \Rightarrow c.\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2a}}\) (1)
Lại có \({c^2} = {a^2} + {b^2} - 2ab.\cos C\)\( \Rightarrow b\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2a}}\) (2)
Từ (1) và (2) cộng vế với vế ta được: \(b.\cos C + c.\cos B = \frac{{2{a^2}}}{{2a}} = a\).
Vậy đẳng thức đã cho được chứng minh.
Câu 2:
Xem đáp án
Hướng dẫn giải
Theo định lý sin ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
\( \Rightarrow \frac{{{a^2}}}{{{{\sin }^2}A}} = \frac{{{b^2}}}{{{{\sin }^2}B}} = \frac{{{c^2}}}{{{{\sin }^2}C}} = \frac{{{b^2} - {c^2}}}{{{{\sin }^2}B - {{\sin }^2}C}}\) (1)
Thay \({a^2} = 2\left( {{b^2} - {c^2}} \right)\) vào (1) ta được:
\(\frac{{2\left( {{b^2} - {c^2}} \right)}}{{{{\sin }^2}A}} = \frac{{{b^2} - {c^2}}}{{{{\sin }^2}B - {{\sin }^2}C}}\)\( \Leftrightarrow \frac{2}{{{{\sin }^2}A}} = \frac{1}{{{{\sin }^2}B - {{\sin }^2}C}}\)
Suy ra \({\sin ^2}A = 2\left( {{{\sin }^2}B - {{\sin }^2}C} \right)\).
Câu 3:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Áp dụng định lý hệ quả sin ta có \(\sin A = \frac{a}{{2R}}\), \(\sin B = \frac{b}{{2R}}\), \(\sin C = \frac{c}{{2R}}\).
Do đó ta có: sin2A = sinB.sinC \( \Leftrightarrow {\left( {\frac{a}{{2R}}} \right)^2} = \frac{b}{{2R}}.\frac{c}{{2R}}\)\( \Leftrightarrow {a^2} = bc\).
Câu 4:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Theo định lí sin trong tam giác ABC ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
Suy ra \(\sin A = \frac{{a.\sin C}}{c}\); \(\sin B = \frac{{b.\sin C}}{c}\).
Lại có: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\); \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\).
Do đó: \[\tan A = \frac{{\sin A}}{{\cos A}} = \frac{{\frac{{a.\sin C}}{c}}}{{\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}}} = \frac{{2ab\sin C}}{{{b^2} + {c^2} - {a^2}}}\]
\[\tan B = \frac{{\sin B}}{{\cos B}} = \frac{{\frac{{b.\sin C}}{c}}}{{\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}}} = \frac{{2ab\sin C}}{{{a^2} + {c^2} - {b^2}}}\].
Vậy \[\frac{{\tan A}}{{\tan B}} = \frac{{{c^2} + {a^2} - {b^2}}}{{{c^2} + {b^2} - {a^2}}}\].
Câu 5:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
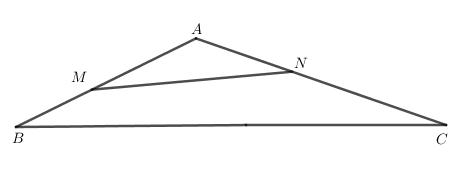
Diện tích tam giác AMN là: \({S_{AMN}} = \frac{1}{2}.AM.AN.\sin \widehat {MAN}\).
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat {BAC}\).
Do \(\widehat {MAN} = \widehat {BAC}\) (hai góc trùng nhau)
Nên \(\frac{{{S_{AMN}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AB}}.\frac{{AN}}{{AC}}\).
Câu 6:
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Áp dụng công thức tính diện tích tam giác ta có:
\(S = \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B\)
Suy ra: \(\sin A = \frac{{2S}}{{bc}}\); \(\sin B = \frac{{2S}}{{ac}}\); \(\sin C = \frac{{2S}}{{ab}}\).
Lại có: \(\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\); \(\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\).
Do đó, ta có:
sin B. cos C + sin C. cos B
= \(\frac{{2S}}{{ac}}.\frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} + \frac{{2S}}{{ab}}.\frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\)
\( = \frac{S}{{{a^2}bc}}\left( {{a^2} + {b^2} - {c^2} + {a^2} + {c^2} - {b^2}} \right)\)
\( = \frac{S}{{{a^2}bc}}.2{a^2} = \frac{{2S}}{{bc}} = \sin A\).
Vậy sinA = sin B. cos C + sin C. cos B.
Câu 7:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Áp dụng công thức tính diện tích tam giác ta có: \(S = \frac{1}{2}bc\sin A\)
Suy ra: \(\sin A = \frac{{2S}}{{bc}}\).
Theo hệ quả định lí côsin ta có: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\).
Do đó: \(\cot A = \frac{{\cos A}}{{\sin A}} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}:\frac{{2S}}{{bc}} = \frac{{{b^2} + {c^2} - {a^2}}}{{4S}}\).
Câu 8:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Theo định lí sin trong tam giác ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra a = 2R.sin A; b = 2R.sin B; c = 2R.sin C.
Lại có: \(S = \frac{{abc}}{{4R}} = \frac{{2R.\sin A.2R.\sin B.2R.\sin C}}{{4R}}\) = \(2{R^2}.\sin A.\sin B.\sin C\).
Câu 9:
Cho tam giác ABC có BC = a, AC = b, AB = c. Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Trong tam giác ABC, theo định lý côsin ta có:
b2 = a2 + c2 − 2ac.cosB;
c2 = a2 + b2 − 2ab.cosC.
Do đó ta có:
b2 – c2 = (a2 + c2 − 2ac.cosB) – (a2 + b2 − 2ab.cosC)
⇔ b2 – c2 = c2 – b2 – 2ac.cosB + 2ab.cosC
⇔ 2b2 – 2c2 = 2a(b.cosC – c.cosB)
⇔ b2 – c2 = a(b.cosC – c.cosB).
Vậy b2 – c2 = a(b.cosC – c.cosB).
Câu 10:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Theo định lý sin ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Suy ra: \(\sin A = \frac{a}{{2R}}\); \(\sin B = \frac{b}{{2R}}\); \(\sin C = \frac{c}{{2R}}\).
Do đó: sin A + sin B + sin C = \(\frac{{a + b + c}}{{2R}}\).
Câu 11:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Theo định lý sin ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Do đó: \(\sin A = \frac{a}{{2R}}\); \(\sin B = \frac{b}{{2R}}\); \(\sin C = \frac{c}{{2R}}\).
Ta có: 2sin B – 2sin C = 2.\(\frac{b}{{2R}}\) − 2.\(\frac{c}{{2R}}\) = \(\frac{{b - c}}{R}\).
Mà b – c = \(\frac{a}{2}\) hay a = 2(b – c) nên sinA = \(\frac{a}{{2R}}\)= \(\frac{{2\left( {b - c} \right)}}{{2R}} = \frac{{b - c}}{R}\).
Vậy sinA = 2sinB – 2sinC.
Câu 12:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Theo định lý sin ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Do đó: \(\sin A = \frac{a}{{2R}}\); \(\sin B = \frac{b}{{2R}}\); \(\sin C = \frac{c}{{2R}}\).
Ta có: sin B + sin C = \(\frac{b}{{2R}}\) + \(\frac{c}{{2R}}\) = \(\frac{{b + c}}{{2R}}\).
Mà b + c = 2a nên 2sin A = \(\frac{{2a}}{{2R}}\)= \(\frac{{b + c}}{{2R}}\).
Vậy 2 sin A = sin B + sin C.