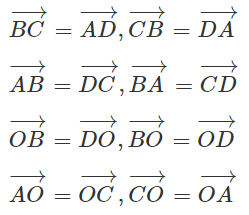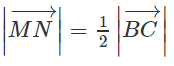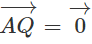Bài 1: Các định nghĩa - SBT Hình học 10
-
3098 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hãy tính số các vectơ (khác )mà các điểm đầu và điểm cuối được lấy từ các điểm phân biệt đã cho trong các trường hợp sau:
a) Hai điểm
b) Ba điểm;
c) Bốn điểm.
Xem đáp án
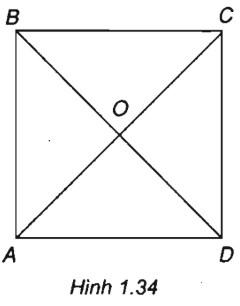
a) Với hai điểm A, B có hai vec tơ 
b) Với ba điểm A, B, C có 6 vec tơ 
c) Với bốn điểm A, B, C, D có 12 véctơ. Học sinh tự liệt kê theo quy tắc: hai điểm tạo thành 2 vectơ đối nhau.
Câu 3:
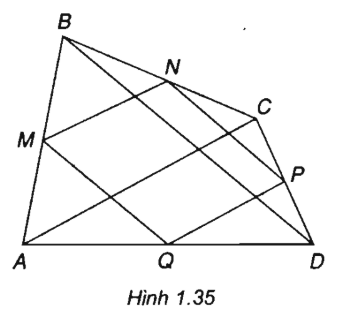
Cho tứ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA. Chứng minh và
Xem đáp án
(h. 1.35)
MN = PQ và MN // PQ
Vì chúng đều bằng 0,5AC và đều song song với AC .
Vậy tứ giác MNPQ là hình bình hành nên ta có:
Câu 4:
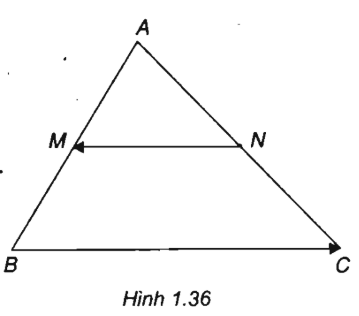
Cho tam giác ABC. Các điểm M và N lần lượt là trung điểm của các cạnh AB và AC. So sánh độ dài của hai vec tơ và . Vì sao có thể nói hai vec tơ này cùng phương?
Xem đáp án
(h. 1. 36)
MN // BC và MN = 1/2 BC hay 
Vì MN // BC nên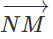 
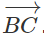
và 
cùng phương.
Câu 5:
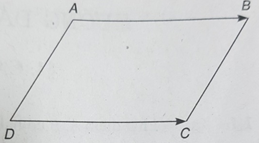
Cho tứ giác ABCD, chứng minh rằng nếu AB→ = CD→ thì AD→ = BC→
Xem đáp án
Tứ giác ABCD có AB→ = CD→ nên AB = DC và AB // CD.
Do đó ABCD là hình bình hành, suy ra: AD→ = BC→.
Câu 6:
Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau:
a) cùng hướng,
b) ngược hướng;
c) cùng phương.
Xem đáp án
a) Nếu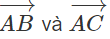 
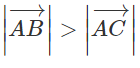
cùng hướng, 
thì điểm C nằm giữa hai điểm A và B (h.1.38)
b) Nếu 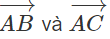ngược hướng thì điểm A nằm giữa hai điểm B và C (h. 1.39)
c) Nếu 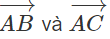cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
Trường hợp 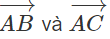cùng hướng
- Nếu 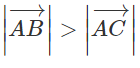thì C nằm giữa A và B.
- Nếu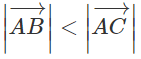 
thì B nằm giữa A và C.
Trường hợp Trường hợp 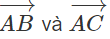ngược hướng thì A nằm giữa B và C.
Câu 7:
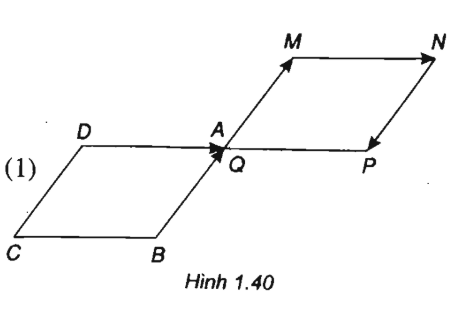
Cho hình bình hành ABCD. Dựng . Chứng minh
Xem đáp án
(h.1.40)
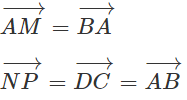
Suy ra AM = NP và AM // NP. Vậy tứ giác AMNP là hình bình hành. (1)
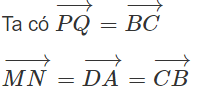
Suy ra PQ = MN và P Q // MN . Vậy tứ giác MNPQ là hình bình hành (2).
Từ (1) và (2) suy ra A = Q hay
