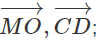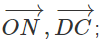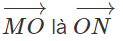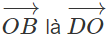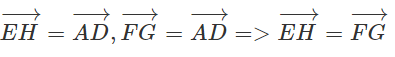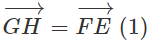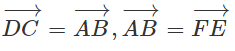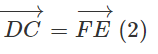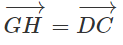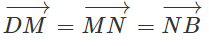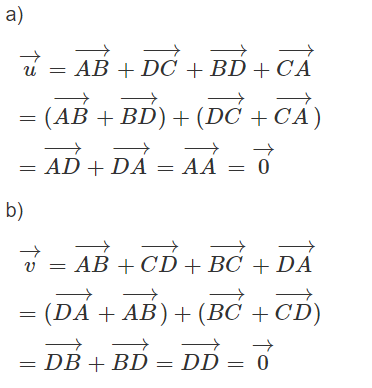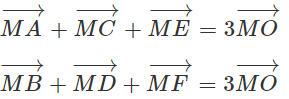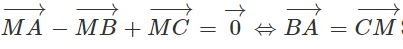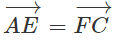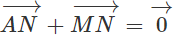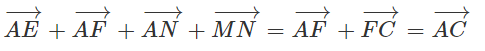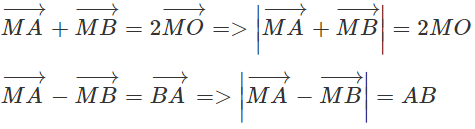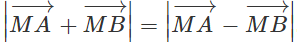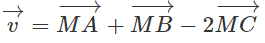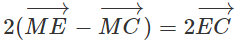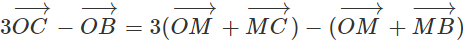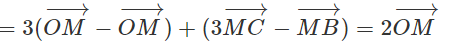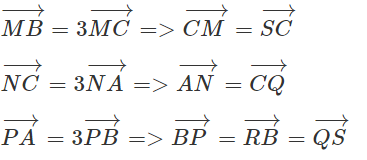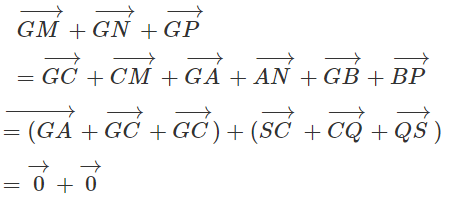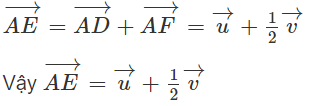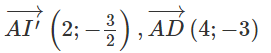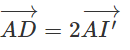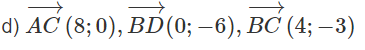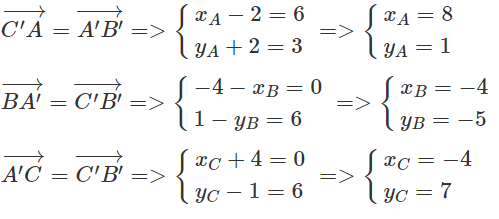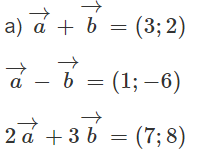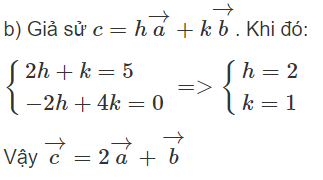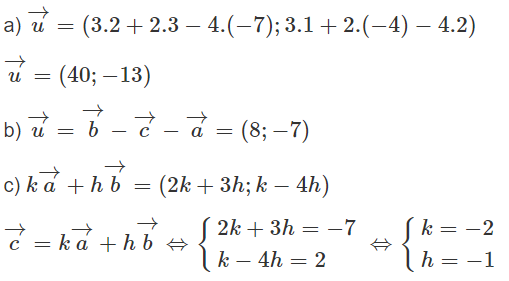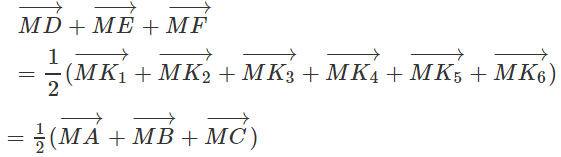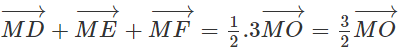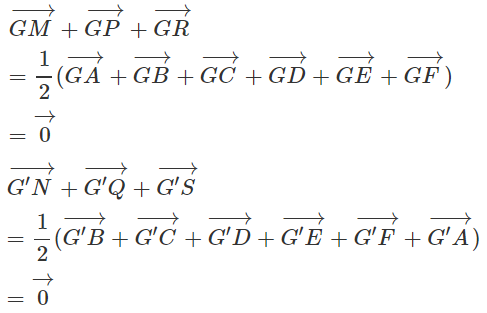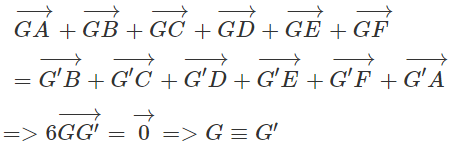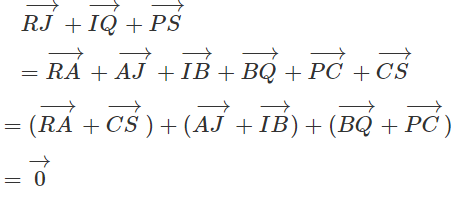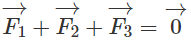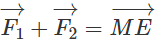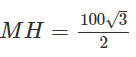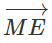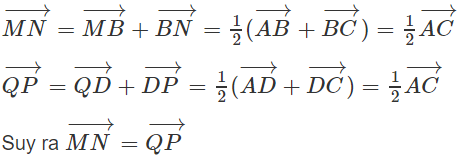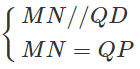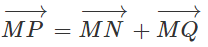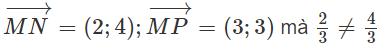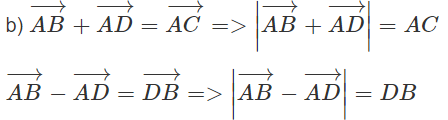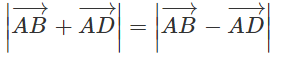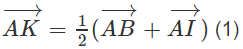Ôn tập chương 1 - SBT Hình học 10
-
3097 lượt thi
-
53 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
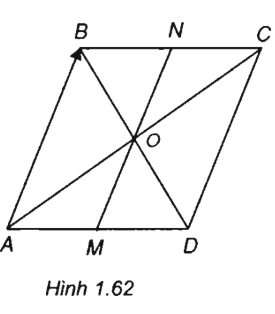
Cho hình bình hành ABCD tâm O. Gọi M và N lần lượt là trung điểm của AD và BC. Dựa vào các điểm A, B, C, D, O, M, N đã cho, hãy:
a) Kể tên hai vec tơ cùng phương với , hai vec tơ cùng hướng với , hai vec tơ ngược hướng với (các vec tơ kể ra này đều khác )
b) Chỉ ra một vec tơ bằng vec tơ ) , một vec tơ )
 Xem đáp án
Xem đáp án
(Xem h.162)
a) Hai vec tơ cùng phương với 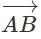
Hai vec tơ cùng hướng với 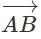
Hai vec tơ ngược hướng với 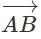
b) Vec tơ
Vec tơ
Câu 2:
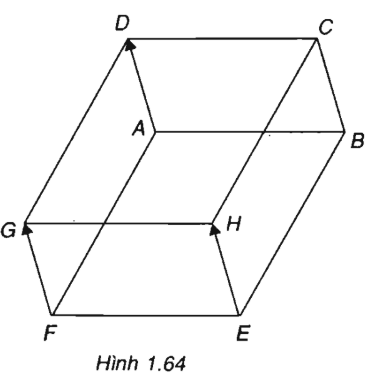
Cho hai hình bình hành ABCD và ABEF với A, D, F không thẳng hàng. Dựng các vec tơ và bằng vec tơ Chứng minh tứ giác CDGH là hình bình hành.
 Xem đáp án
Xem đáp án
(h.1.64)
⇒Tứ giác FEHG là hình bình hành
⇒
Ta có:
⇒
Từ (1) và (2) ta có
Vậy tứ giác GHCD là hình bình hành.
Câu 3:
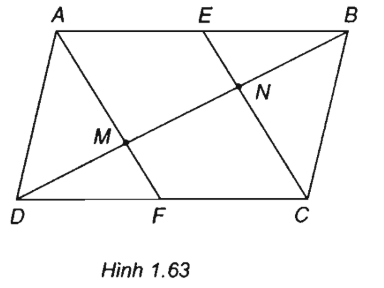
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của hai cạnh AB và CD. Nối AF và CE, hai đường thẳng này cắt đường chéo BD lần lượt tại M và N. Chứng minh
 Xem đáp án
Xem đáp án
(h.1.63)
AECF là hình bình hành ⇒ EN // AM
E là trung điểm của AB ⇒ N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy
Câu 5:
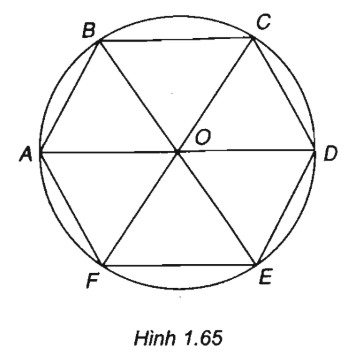
Cho lục giác đều ABCDEF và M là một điểm tùy ý. Chứng minh rằng:
 Xem đáp án
Xem đáp án
(h.1.65)
Gọi O là tâm lục giác đều. Khi đó O là trọng tâm của các tam giác đều ACE và BDF.
Do đó, với mọi điểm M ta có:
Vậy ta có đẳng thức cần chứng minh.
Câu 6:
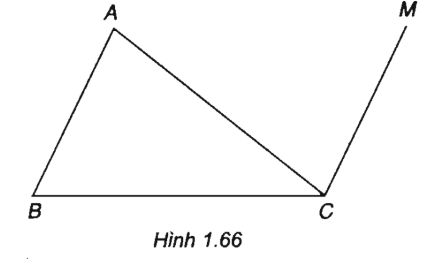
Cho tam giác ABC. Tìm điểm M thỏa mãn điều kiện:
 Xem đáp án
Xem đáp án
(h.1.66)
M là đỉnh của hình bình hành ABCM.
Câu 7:
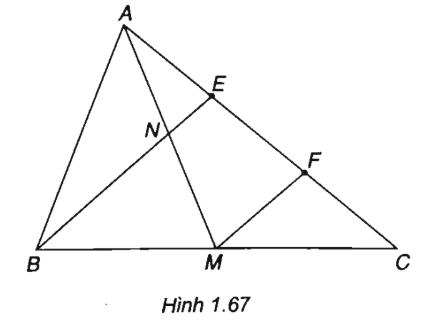
Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC. BE cắt trung tuyến AM tại N. Tính:
 Xem đáp án
Xem đáp án
(h.1.67)
Ta có
Vì MF // BE nên N là trung điểm của AM, suy ra
Do đó
Câu 8:
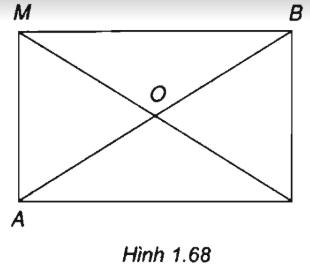
Cho hai điểm A và B. Điểm M thỏa mãn điều kiện Chứng minh rằng: OM = AB/2, trong đó O là trung điểm của AB.
 Xem đáp án
Xem đáp án
(h.1.68)
Vậy 2MO = AB hay OM = AB/2.
Chú ý: Tập hợp các điểm M có tính chất
là đường tròn đường kính AB.
Câu 9:
Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vec tơ không phụ thuộc vào vị trí của điểm M. Hãy xác định điểm D sao cho .
 Xem đáp án
Xem đáp án
= 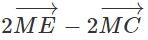
=
Vậy 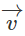
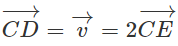
Câu 10:
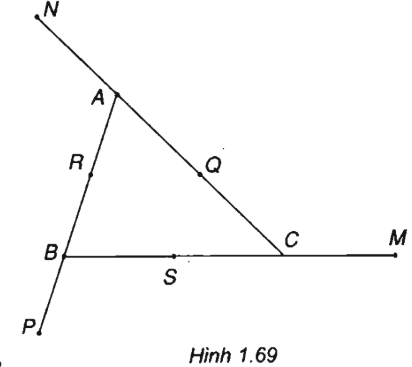
Cho tam giác ABC. Gọi M, N , P là những điểm được xác định như sau:
a) Chứng minh với mọi điểm O.
b) Chứng minh hai tam giác ABC và MNP có cùng trọng tâm.
 Xem đáp án
Xem đáp án
(Xem h.1.69)
a)
b) Gọi S, Q và R lần lượt là trung điểm của BC, CA và AB.
Gọi G là trọng tâm của tam giác ABC thì
Ta có:
Vậy G là trọng tâm của tam giác MNP.
Câu 11:
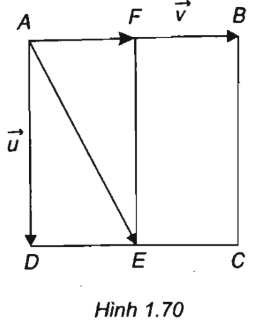
Cho hình vuông ABCD, E là trung điểm của CD. Hãy phân tích theo hai vectơ
 Xem đáp án
Xem đáp án
(h.1.70)
Gọi F là trung điểm của cạnh AB. Ta có
Câu 13:
ho hình thoi ABCD tâm O có AC = 8, BD = 6. Chọn hệ tọa độ sao cho cùng hướng, cùng hướng
a) Tìm tọa độ các đỉnh của hình thoi;
b) Tìm tọa độ trung điểm I của BC và trọng tâm của tam giác ABC;
c) Tìm tọa độ điểm đối xứng I' của I qua tâm O. Chứng minh A, I', D thẳng hàng
d) Tìm tọa độ của vec tơ
 Xem đáp án
Xem đáp án
(Xem h.1.71)
a) Ta có: AO = OC = 4 và OB = OD = 3
⇒ A(-4; 0), C(4; 0), B(0; 3), D(0; -3)
b) I là trung điểm BC ⇒ I(2; 3/2)
G là trọng tâm tam giác ABC ⇒ G(0; 1)
c) I' đối xứng với I qua O ⇒ I'(-2; -2/3)
Ta có
Vậy
Vậy A, I', D thẳng hàng
Câu 14:
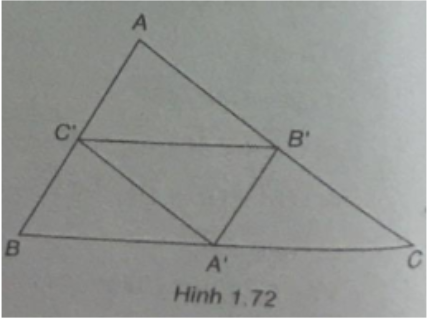
Cho các điểm A'(-4;1), B'(2;4) và C'(2; - 2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC.
a) Tính tọa độ các đỉnh của tam giác ABC;
b) Chứng minh rằng các trọng tâm của các tam giác ABC và A'B'C' trùng nhau.
 Xem đáp án
Xem đáp án
(Xem hình 1.72)
a)
b) Tính tọa độ trọng tâm G, G' của tam giác ABC và A'B'C' ta được G(0;1) và G'(0;1).
Vậy G=G'
Câu 17:
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng:
 Xem đáp án
Xem đáp án
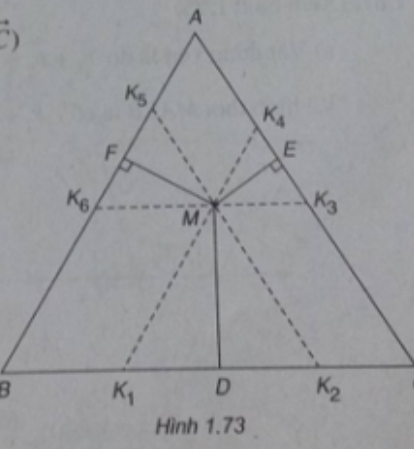
(Xem hình 1.73)
Qua M kẻ các đường thẳng sau: K1K4 // AB, K2K5 // AC, K3K6 // BC
K1, K2 ∈ BC, K3, K4 ∈ AC, K5, K6 ∈ AB. Ta có
(Vì MK5AK4, MK3CK2, MK1BK6) là các hình bình hành). Vậy
Câu 18:
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
 Xem đáp án
Xem đáp án
Gọi G và G' lần lượt là trọng tâm các tam giác MPR và NQS. Ta có:
Do đó
Câu 19:
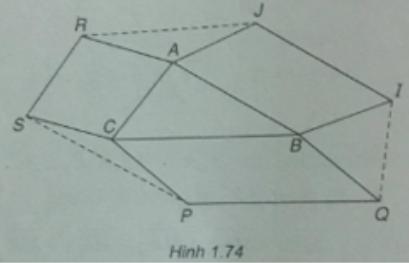
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng:
 Xem đáp án
Xem đáp án
(Xem hình 1.74)
Câu 20:
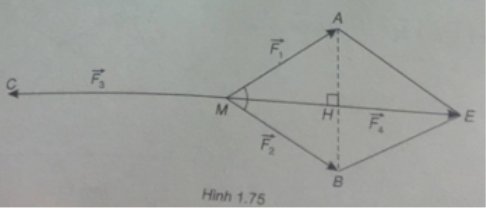
Cho ba lực: cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của F1 và F2 đều là 100 N và góc AMB = 60ο
a) Đặt Tính độ dài của đoạn ME
b) Tìm cường độ và hướng của lực F3
 Xem đáp án
Xem đáp án
(Xem hình 1.75)
a) Vật đứng yên là do
Vẽ hình thoi MAEB ta có:
Tam giác MAB là tam giác đều có đường cao
Suy ra ME = 100√3
b) Lực 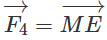
Ta có 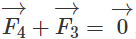
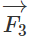
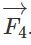
Như vậy 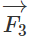
Câu 21:
Cho tứ giác ABCD.Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA.
Chứng minh rằng:
 Xem đáp án
Xem đáp án
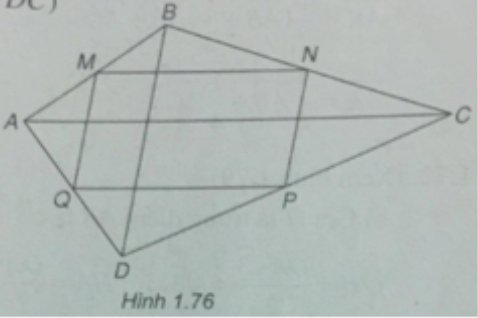
(Xem hình 1.76)
a) Ta có:
b) Tứ giác MNPQ có:
Suy ra MNPQ là hình bình hành.
Suy ra
Câu 22:
Xét xem ba điểm sau có thẳng hàng không?
a) A(2; - 3), B(5;1) và C(8; 5);
b) M(1;2), N(3; 6) và P(4;5).
 Xem đáp án
Xem đáp án
a)
Ta có
⇒ A, B, C thẳng hàng.
b)
Câu 23:
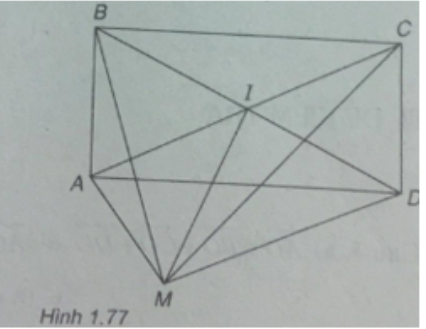
Cho hình chữ nhật ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.
a) Với điểm M tùy ý, hãy chứng minh:
b) Chứng minh rằng:
 Xem đáp án
Xem đáp án
(Xem hình 1.77)
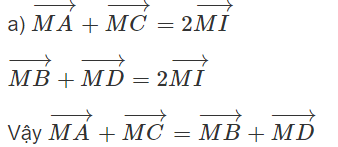
Vì hai đường chéo của hình chữ nhật dài bằng nhau nên
Câu 24:
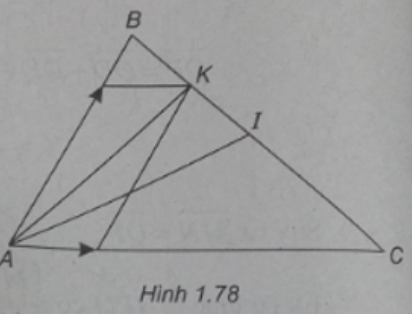
Cho tam giác ABC. Gọi I là trung điểm của BC, K là trung điểm của BI.
Chứng minh rằng:
 Xem đáp án
Xem đáp án
(Xem hình 1.78)
a) Vì K là trung điểm của BI nên
b) Vì I là trung điểm của BC nên
Thay (2) vào (1) ta được:
Câu 25:
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Vì hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
Đáp án: D
Câu 26:
Nếu hai vectơ bằng nhau thì chúng
 Xem đáp án
Xem đáp án
Vì hai vectơ bằng nhau thì cùng độ dài và cùng hướng.
Đáp án: C
Câu 27:
Số các vectơ có điểm đầu và điểm cuối là 2 trong 6 điểm phân biệt cho trước là:
 Xem đáp án
Xem đáp án
Với mỗi cặp hai điểm ta có 2 vectơ. Với 6 điểm phân biệt có 15 cặp điểm khác nhau.
Đáp án: D
Câu 28:
Số các vectơ có điểm đầu là một trong 5 điểm phân biệt cho trước và có điểm cuối là một trong bốn điểm phân biệt cho trước là:
 Xem đáp án
Xem đáp án
Vì với mỗi điểm trong 5 điểm đầu ta có 4 vectơ.
Đáp án: A
Câu 30:
Cho các vectơ có cùng độ dài bằng 5 và cùng phương, hãy chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Tổng hai vectơ đối là 0→.
Đáp án: B
Câu 31:
Nếu là các vectơ khác là đối vectơ đối của thì chúng:
Hãy chọn khẳng định sai.
 Xem đáp án
Xem đáp án
Vì hai vectơ đối nhau khi và chỉ khi cùng độ dài và ngược hướng.
Đáp án: D
Câu 34:
Cho hình bình hành ABCD tâm O. Tìm khẳng định sai trong các khẳng định sau:
 Xem đáp án
Xem đáp án
Vì AO→ và BO→ không cùng phương.
Đáp án: C
Câu 35:
Cho G là trọng tâm của tam giác ABC và I là trung điểm của BC. Hãy chọn đẳng thức đúng.
 Xem đáp án
Xem đáp án
Đáp án: B
Câu 36:
Cho tam giác ABC, E là điểm trên cạnh BC sao cho BE = BC/4. Hãy chọn đẳng thức đúng.
 Xem đáp án
Xem đáp án
Khi phân tích AE→ = hAB→ + kAC→ thì hai số h, k không thể lớn hơn 1, không có số âm và không thể bằng nhau.
Đáp án: B
Câu 37:
Cho tam giác ABC, I là trung điểm của BC, M là một điểm tùy ý. Điểm G là trong tâm tam giác ABC nếu:
Hãy chọn khẳng định sai
 Xem đáp án
Xem đáp án
Vì G có thể không thuộc AI.
Đáp án: A
Câu 38:
Cho hai điểm A, B. Điểm M thuộc đoạn thẳng AB nếu:
Hãy chọn khẳng định sai.
 Xem đáp án
Xem đáp án
Vì từ -3MA→ + 3/4 MB→ = 0 ⃗ suy ra MA→ = 1/4 MB→ mà hai vectơ MA→, 1/4 MB→ ngược hướng.
Đáp án: D
Câu 39:
Cho ba điểm không thẳng hàng A, B, C. Điểm D là đỉnh thứ tư của hình bình hành ABCD khi và chỉ khi:
Hãy chọn khẳng định sai.
 Xem đáp án
Xem đáp án
Vì với mọi D đều có DB→ - DC→ = CB→.
Đáp án: C
Câu 40:
Xét trong mặt phẳng Oxy Cho A(-1; 0), B(0; 5), C(3; 1), D(1; -5) và M là một điểm tùy ý. Tọa độ điểm G có tính chất là:
 Xem đáp án
Xem đáp án
Vì GA→ + GB→ + GC→ + GD→ = 0 ⃗.
Đáp án: D
Câu 41:
Xét trong mặt phẳng Oxy. Cho . Hãy chọn khẳng định đúng
 Xem đáp án
Xem đáp án
Đáp án: D
Tính tọa độ của a→ + b→ và a→ - b→. Ta thấy c→ = -2(a→ + b→).
Câu 42:
Cho ba điểm A(0; 3), B(1; 5), C(-3; -3). Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
AB→ = (1;2), AC→ = (-3; -6).
Đáp án: B
Câu 43:
Cho tam giác ABC có A(1; -3), B(2; 5), C(0; 7). Trọng tâm của tam giác ABC là điểm có tọa độ:
 Xem đáp án
Xem đáp án
Tổng ba hoành độ và ba tung độ của ba đỉnh đều khác không và tọa độ không thể là √2.
Đáp án: D
Câu 44:
Cho hai điểm A(3; -5), B(1; 7). Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Vì nếu A(x1 ; y1 ), B(x2 ; y2 ) thì AB→ = (x2 - x1 ; y2 - y1 ) và trung điểm I((x1 + x2 )/2, (y1 + y2 )/2).
Đáp án: C
Câu 45:
Cho . Tọa độ của vectơ là:
 Xem đáp án
Xem đáp án
Sử dụng công thức tọa độ của phép nhân vectơ với một số và phép trừ vectơ.
Đáp án: B
Câu 46:
Cho tam giác ABC, trung điểm của các cạnh BC, CA và AB có tọa độ lần lượt là M(1; -1), N(3; 2), P(0; -5). Tọa độ của điểm A là:
 Xem đáp án
Xem đáp án
Kiểm tra đẳng thức PA→ = MN→ bằng tọa độ.
Đáp án: A
Câu 47:
Cho hình bình hành ABCD có A(-2; 3), B(0; 4), C(5; -4). Tọa độ đỉnh D là:
 Xem đáp án
Xem đáp án
Kiểm tra đẳng thức BA→ = CD→ bằng tọa độ.
Đáp án: B
Câu 48:
Cho M(5; -3). Kẻ MM1 vuông góc với Ox, MM2 vuông góc với Oy. Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Khẳng định đúng là D vì OM→ = OM1→ + OM2→ và tọa độ của M là tọa độ của vectơ OM→
Đáp án: D
Câu 49:
Cho bốn điểm A(0; 1), B(-1; -2), C(1; 5), D(-1; -1) Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Vì AB→ = (-1; -3), BC→ = (2;7), AD→ = (-1; -2), CD→ = (-2; -6).
Đáp án: B
Câu 50:
là hai vectơ đơn vị của hệ trục tọa độ . Tọa độ của vectơ là:
 Xem đáp án
Xem đáp án
Nhận xét rằng tọa độ của 2i→ + j→ không thể là số âm và số vô tỉ.
Đáp án: C
Câu 51:
Cho tam giác ABC có trọng tâm là gốc tọa độ, biết tọa độ hai đỉnh là A(-3; 5), B(0; 4). Tọa độ của đỉnh C là:
 Xem đáp án
Xem đáp án
Tổng các hoành độ và tung độ của ba đỉnh phải bằng 0.
Đáp án: C
Câu 52:
Trong mặt phẳng Oxy, cho tam giác đều OAB có AB = 2, AB song song với Ox. Điểm A có hoành độ và tung độ dương. Ta có:
Hãy chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Vì A, B có cùng tọa độ và hoành độ lần lượt là 1 và -1.
Đáp án: B