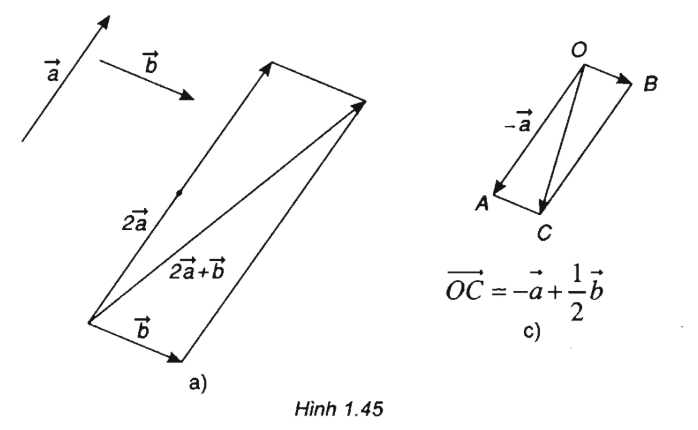
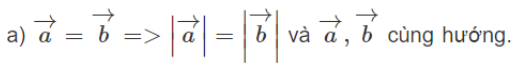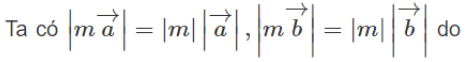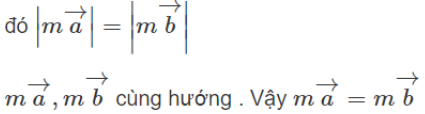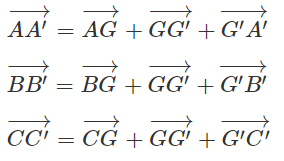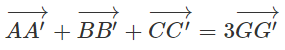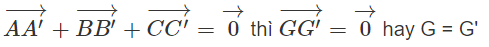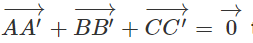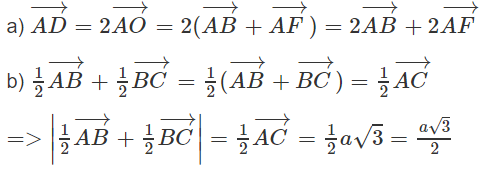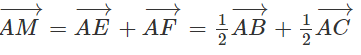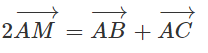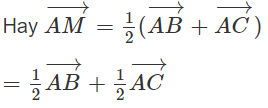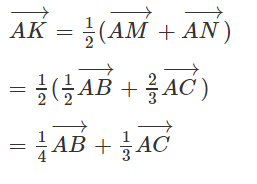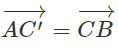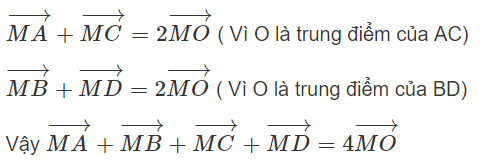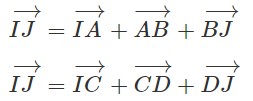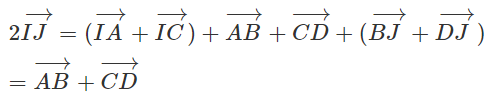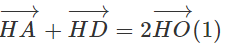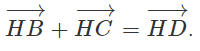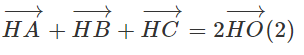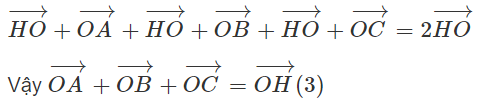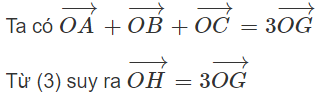16 câu hỏi trắc nghiệm thuộc Bài 3: Tích của vectơ với một số - SBT Hình học 10 - hamchoi.vn

Giải SBT Toán 10 Hình học - Chương 1: Vectơ

Bài 3: Tích của vectơ với một số - SBT Hình học 10

3099 lượt thi
16 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tìm giá trị của m sao cho $\vec{a} = m \vec{b}$ trong các trường hợp sau:

$a) \vec{a} = \vec{b} \neq \vec{0} b) \vec{a} = \vec{- b} và \vec{a} \neq \vec{0} c) \vec{a}, \vec{b} cùng hướng và |\vec{a}| = 20, |\vec{b}| = 5 d) \vec{a}, \vec{b} ngược hướng và |\vec{a}| = 5, |\vec{b}| = 15 e) \vec{a} = \vec{0}, \vec{b} \neq \vec{0} g) \vec{a} \neq \vec{0}, \vec{b} = \vec{0} h) \vec{a} = \vec{0}, \vec{b} = \vec{0}$

Câu 2:

Chứng minh rằng:

$a) Nếu \vec{a} = \vec{b} thì m \vec{a} = m \vec{b} b) m \vec{a} = m \vec{b} và m \neq 0 thì \vec{a} = \vec{b} c) Nếu m \vec{a} = n \vec{a} và \vec{a} \neq 0 thì m = n$

Câu 3:

Chứng minh rằng tổng của n véc tơ $\vec{a}$ bằng n $\vec{a}$ (n là số nguyên dương).

Câu 4:

Cho tam giác ABC. Chứng minh rằng nếu $\vec{GA} + \vec{GB} + \vec{GC} = \vec{0}$ thì G là trọng tâm của tam giác ABC.

⇔

⇔

Từ đó suy ra ba điểm A, G, I thẳng hàng, trong đó GA = 2GI, G nằm giữa A và I.

Vậy G là trọng tâm của tam giác ABC.

Câu 5:

Cho hai tam giác ABC và A'B'C'. Chứng minh rằng nếu $\vec{AA'} + \vec{BB'} + \vec{CC'} = \vec{0}$ thì hai tam giác đó có cùng trọng tâm.

Gọi G và G' lần lượt là trọng tâm của hai tam giác ABC và A'B'C'. Ta có:

Cộng từng vế của ba đẳng thức trên ta được

Do đó, nếu

Chú ý: Từ chứng minh trên cũng suy ra rằng nếu hai tam giác ABC và A'B'C' có cùng trọng tâm thì

Câu 6:

Cho hai vec tơ không cùng phương $\vec{a} và \vec{b}$ Dựng các vec tơ:

$a) 2 \vec{a} + \vec{b} b) \vec{a} - 2 \vec{b} c) - \vec{a} + \frac{1}{2} \vec{b}$

(Xem h.1. 45)

Hãy vẽ trường hợp

Câu 7:

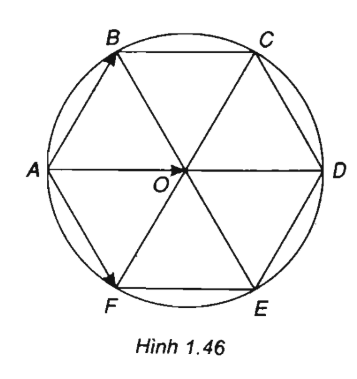
Cho lục giác đều ABCDEF tâm O có cạnh a.

a) Phân tích vec tơ $\vec{AD}$ theo hai vec tơ $\vec{AB} v à \vec{AF}$

b) Tính độ dài của vec tơ $\frac{1}{2} \vec{AB} + \frac{1}{2} \vec{BC}$ theo a.

(Xem h.1.46)

Câu 8:

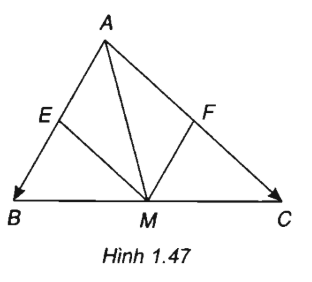
Cho tam giác ABC có trung tuyến $\vec{AM}$ (M là trung điểm của BC). Phân tích vec tơ $\vec{AM}$ theo hai vectơ $\vec{AB} và \vec{AC}$

(h.1.47)

Gọi E, F lần lượt là trung điểm của AB, AC.

Ta có tứ giác AFME là hình bình hành nên

Có thể chứng minh cách khác như sau:

Vì M là trung điểm của BC nên

Câu 9:

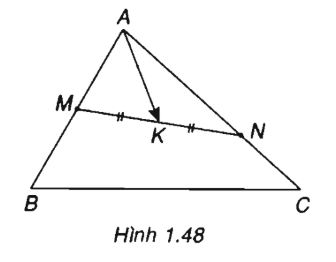
Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2NC. Gọi K là trung điểm của MN.

Phân tích vec tơ $\vec{AK}$ theo $\vec{AB} và \vec{AC}$

(h.1.48)

Câu 10:

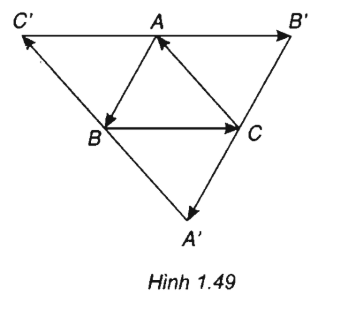
Cho tam giác ABC. Dựng: $\vec{A' B} = \vec{BC}, \vec{C' A} = \vec{AB} và \vec{BC'} = \vec{CA}$

a) Chứng minh rằng A là trung điểm của B'C'

b) Chứng minh các đường thẳng AA', BB', CC' đồng quy

a) ⇒ Tứ giác ACBC' là hình bình hành ⇒

⇒ A là trung điểm của B'C'

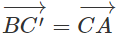
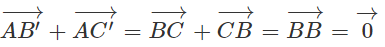
b) Vì tứ giác ACBC' là hình bình hành nên CC' chứa trung tuyến của tam giác ABC xuất phát từ đỉnh C. Tương tự như vậy với AA', BB'. Do đó AA', BB', CC' đồng quy tại trọng tâm G của tam giác ABC.

Câu 11:

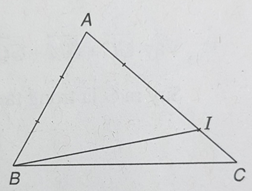
Cho tam giác ABC. Điểm I trên cạnh AC sao cho CI = CA/4, J là điểm mà $\vec{BJ} = \frac{1}{2} \vec{AC} - \frac{2}{3} \vec{AB}$

a) Chứng minh $\vec{BJ} = \frac{3}{4} \vec{AC} - \vec{AB}$

b) Chứng minh B, I, J thẳng hàng.

c) Hãy dựng điểm J thỏa mãn điều kiện đề bài.

a) BI→ = BA→ + AI→ = -AB→ + 3/4 AC→.

b) 2/3 BI→ = 2/3(-AB→ + 3/4 AC→) = (-2)/3 AB→ + 1/2 AC→.

Vậy BJ→ = 2/3 BI→. Suy ra ba điểm B, I, J thẳng hàng.

Học sinh tự dựng điểm J.

Câu 12:

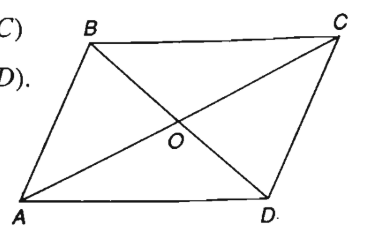
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng với điểm M bất kì ta có

$\vec{MA} + \vec{MB} + \vec{MC} + \vec{MD} = \vec{4 MO}$

(h.1.51)

Câu 13:

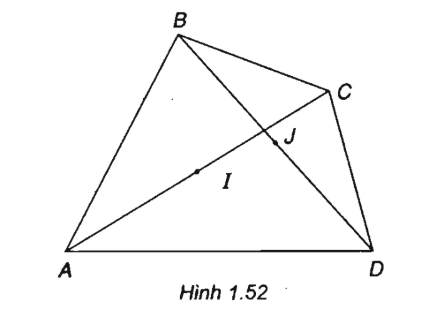
Cho tứ giác ABCD. Gọi I và J lần lượt là trung điểm của hai đường chéo AC và BD. Chứng minh:

$\vec{AB} + \vec{CD} = 2 \vec{IJ}$

(h.1.52)

Cộng từng vế hai đẳng thức trên ta được

Câu 14:

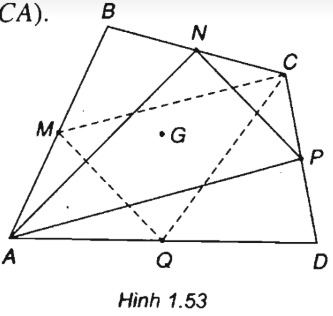
Cho tứ giác ABCD. Các điểm M, N , P và Q lần lượt là trung điểm của AB, BC, CD và DA. Chứng minh rằng hai tam giác ANP và CMQ có cùng trọng tâm.

(h.1.53)

Gọi G là trọng tâm của tam giác ANP.

Khi đó

Ta có:

Suy ra G là trọng tâm của tam giác CMQ.

Câu 15:

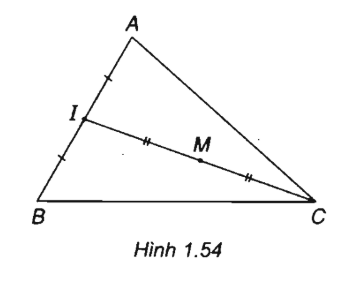
Cho tam giác ABC.

a) Tìm điểm K sao cho $\vec{KA} + 2 \vec{KB} = \vec{CB}$

b) Tìm điểm M sao cho $\vec{MA} + \vec{MB} + \vec{2 MC} = \vec{0}$

(Xem h.1.54)

K là trọng tâm của tam giác ABC.

Câu 16:

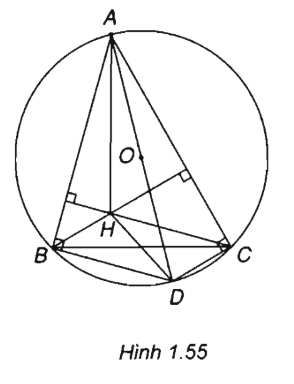
Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O.

a) Chứng minh tứ giác HCDB là hình bình hành.

b) Chứng minh:

$\vec{HA} + \vec{HD} = 2 \vec{HO} \vec{HA} + \vec{HB} + \vec{HC} = 2 \vec{HO} \vec{OA} + \vec{OB} + \vec{OC} = \vec{OH}$

c) Gọi G là trọng tâm tam giác ABC.

Chứng minh $\vec{OH} = 3 \vec{OG}$

Từ đó có kết luận gì về ba điểm O, H, G?

(Xem h.1.55)

a) Vì AD là đường kính của đường tròn tâm O nên BD ⊥ AB, DC ⊥ AC

Ta có CH ⊥ AB, BH ⊥ AC nên suy ra CH // BD và BH // DC

Vậy tứ giác HCDB là hình bình hành.

b) Vì O là trung điểm của AD nên

Vì tứ giác HCDB là hình bình hành nên ta có

Vậy từ (1) suy ra:

Theo quy tắc ba điểm, từ (2) suy ra

c) G là trọng tâm của tam giác ABC.

Vậy ba điểm O, H, G thẳng hàng.

Trong một tam giác trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O thẳng hàng.

Bắt đầu thi ngay

Bài thi liên quan

Các bài thi hot trong chương