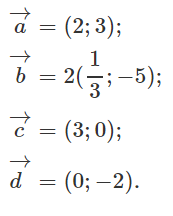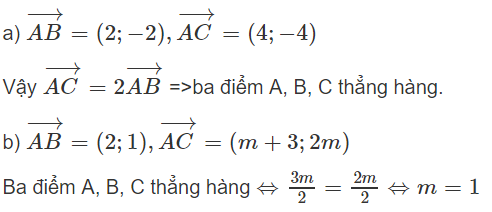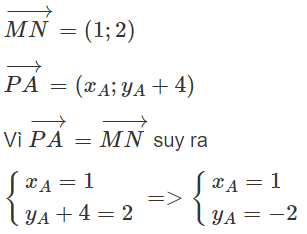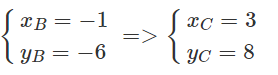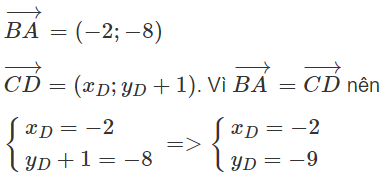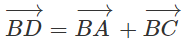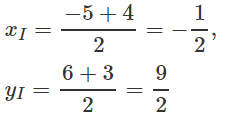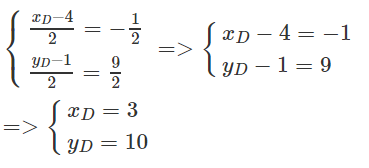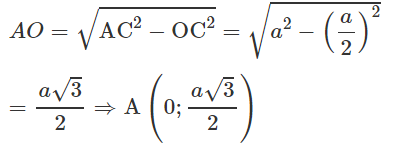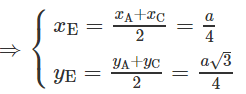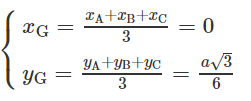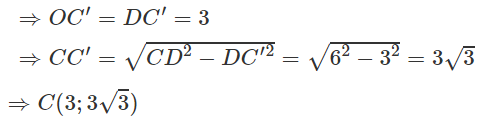Bài 4: Hệ trục tọa độ - SBT Hình học 10
-
3100 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 4:
Xét xem các cặp vec tơ sau có cùng phương không? Trong trường hợp cùng phương thì xét xem chúng cùng hướng hay ngược hướng.
 Xem đáp án
Xem đáp án
a) 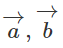
b) 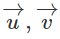
c) 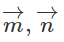
d) 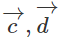
e) 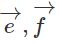
Câu 6:
Cho bốn điểm A(-2; -3), B(3; 7), C(0; 3), D(-4; -5)
Chứng minh rằng hai đường thẳng AB và CD song song với nhau.
 Xem đáp án
Xem đáp án
![]()
Vậy hai đường thẳng AB và CD song song hoặc trùng nhau
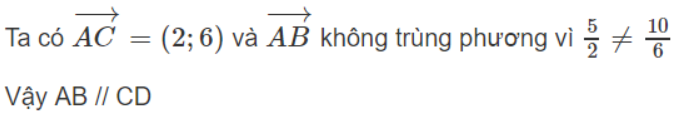
Câu 7:
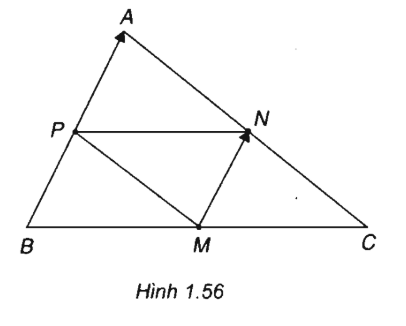
Cho tam giác ABC. Các điểm M(1; 1), N(2; 3), P(0; -4) lần lượt là trung điểm các cạnh BC, CA, AB. Tính tọa độ các đỉnh của tam giác.
 Xem đáp án
Xem đáp án
(h.1.56)
Tương tự, ta tính được
Vậy tọa độ các đỉnh của tam giác là A(11; -2), B(-1; -6), C(3; 8).
Câu 8:
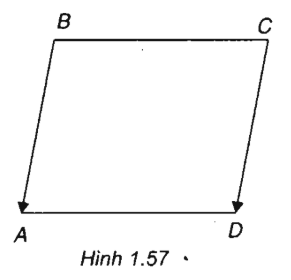
Cho hình bình hành ABCD. Biết A(2; -3), B(4; 5), C(0; -1). Tính tọa độ của đỉnh D
 Xem đáp án
Xem đáp án
(h.1.57)
Vậy tọa độ đỉnh D(-2; -9)
Nhận xét: Ta có thể tính tọa độ đỉnh D dựa vào biểu thức
Câu 9:
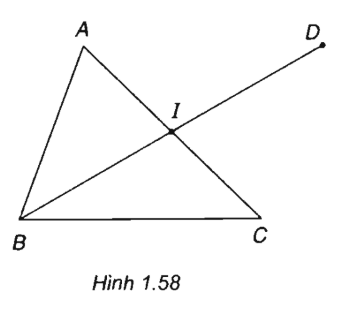
Cho tam giác ABC có A(-5; 6), B(-4; -1), C(4; 3). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
 Xem đáp án
Xem đáp án
(h.1.58)
Gọi I là trung điểm của AC
Tứ giác ABCD là hình bình hành I là trung điểm của BD.
Vậy
Vậy tọa độ đỉnh D là (3;10).
Câu 10:
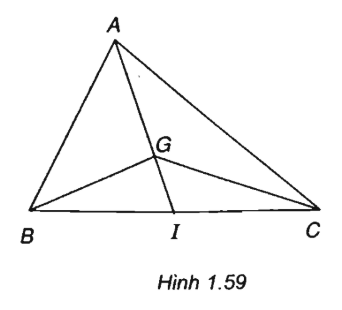
Cho tam giác ABC có A(-3; 6), B(9; -10), C(-5; 4)
a) Tìm tọa độ của trọng tâm G của tam giác ABC
b) Tìm tọa độ điểm D sao cho tứ giác BGCD là hình bình hành.
 Xem đáp án
Xem đáp án
(h.1.59)
a)
b)Tứ giác BGCD là hình bình hành thì tọa độ điểm D là D (11/3; -6)
Câu 11:
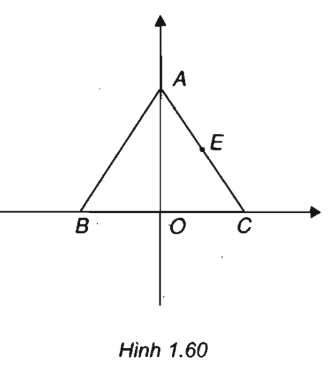
Cho tam giác đều ABC cạnh a. Chọn hệ tọa độ (O; i; j), trong đó O là trung điểm của cạnh BC, vectơ i cùng hướng với vectơ OC, vectơ j cùng hướng với vectơ OA.
a) Tính tọa độ của các đỉnh của tam giác ABC.
b) Tìm tọa độ trung điểm E của AC.
c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
(Xem h.160)
a) Ta có: Tam giác ABC cạnh a mà B là trung điểm BC nên OC = OB = a/2
⇒ C(a/2; 0) và B(-a/2; 0)
b) E là trung điểm AC
c) Do tam giác ABC đều nên tâm đường tròn ngoại tiếp tam giác trùng với trọng tâm G.
Câu 12:
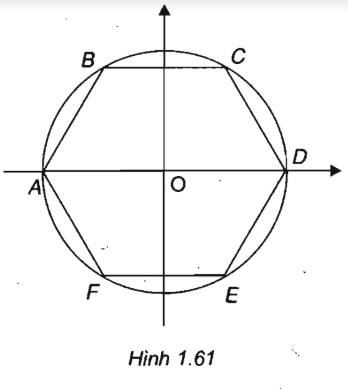
Cho lục giác ABCDEF. Chọn hệ tọa độ (O; i; j), trong đó O là tâm của lục giác đều, hai véc tơ vectơ i và vectơ OD cùng hướng, vectơ j vectơ EC và cùng hướng . Tính tọa độ các đỉnh của lục giác biết độ dài của lục giác là 6.
 Xem đáp án
Xem đáp án
Do ABCDEF là lục giác đều nên AD = 2BC = 12 ⇒ AO = OD = 6
⇒ A(-6; 0), D(6; 0)
Gọi C' là hình chiếu của C trên Ox
B đối xứng với C qua Oy nên B(-3; 3√3)
E đối xứng với C qua Ox nên E(3; -3√3)
F đối xứng với C qua O nên F(-3; -3√3))