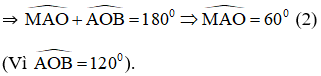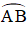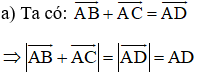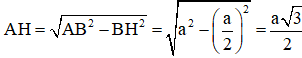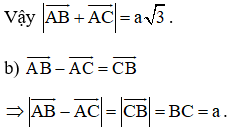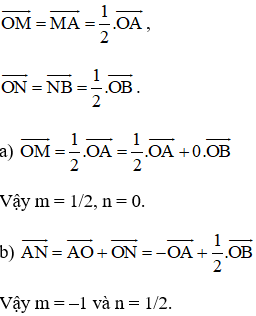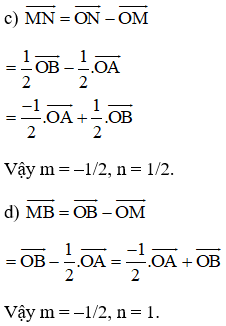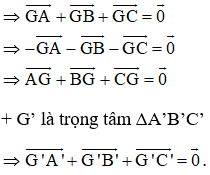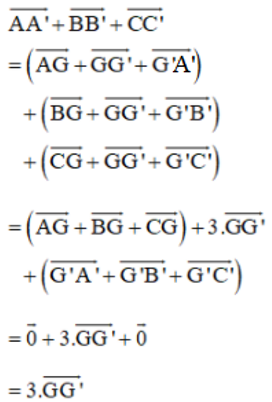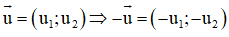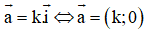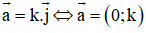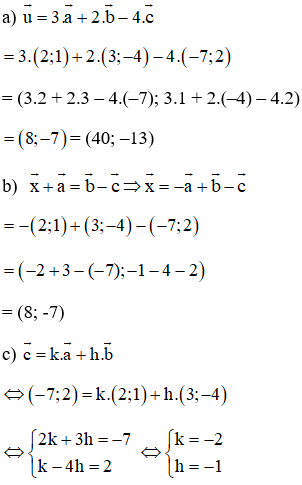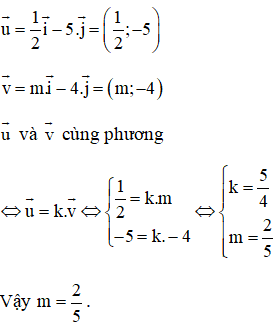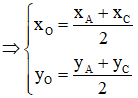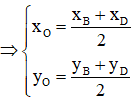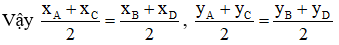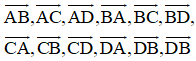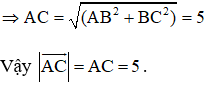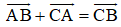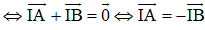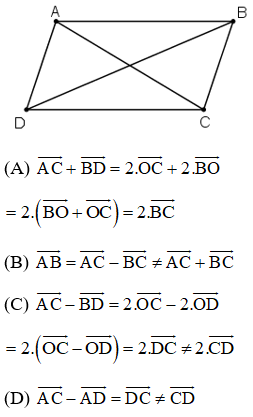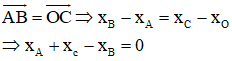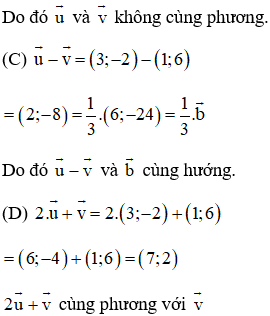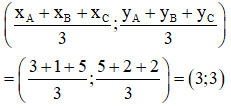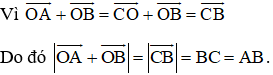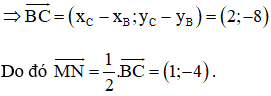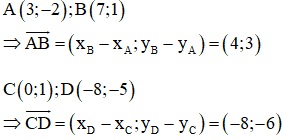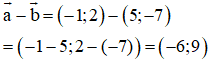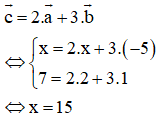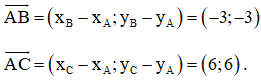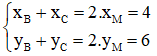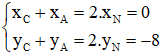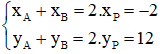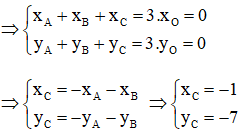42 câu hỏi trắc nghiệm thuộc Ôn tập chương 1

Câu 1:

Cho lục giác đều ABCDEF tâm O. Hãy chỉ ra các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác.

Xem đáp án

Câu 2:

Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?

a, Hai vectơ cùng hướng thì cùng phương.

b, Hai vectơ b→ và kb→ cùng phương.

c, Hai vectơ a→ và (-2)a→ cùng hướng.

d) Hai vectơ ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.

Xem đáp án

a) Đúng

b) Đúng

c) Sai

d) Đúng

Câu 3:

Tứ giác ABCD là hình gì nếu $\vec{A B} = \vec{D C} v à |\vec{A B}| = |\vec{B C}|$

Xem đáp án

tứ giác ABCD là hình bình hành

⇒ tứ giác ABCD là hình thoi.

(Hình bình hành có hai cạnh kề bằng nhau là hình thoi)

Câu 4:

Chứng minh rằng $|\vec{a} + \vec{b}| \leq |\vec{a}| + |\vec{b}|$

Xem đáp án

Câu 5:

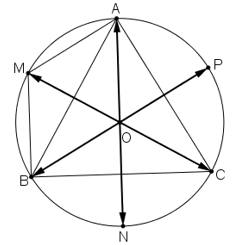
Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:

a) $\vec{O M} = \vec{O A} + \vec{O B}$

b) $\vec{O N} = \vec{O B} + \vec{O C}$

c) $\vec{O P} = \vec{O C} + \vec{O A}$

Xem đáp án

a) 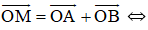M là đỉnh còn lại của hình bình hành AOBM.

+ AOBM là hình bình hành ⇒ AM = OB

Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)

+ AOBM là hình bình hành ⇒ AM//BO

Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.

Mà nên M là điểm chính giữa cung

b) Chứng minh tương tự phần a) ta có: 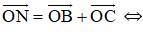N là điểm chính giữa cung BC.

c) P là điểm chính giữa cung CA.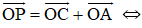

Câu 6:

Cho tam giác đều ABC có cạnh bằng a. Tính:

a) $|\vec{A B} + \vec{A C}|$

b) $|\vec{A B} - \vec{A C}|$

Xem đáp án

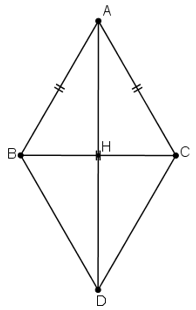
Vẽ hình bình hành ABDC, gọi H là giao điểm của AD và BC.

+ Hình bình hành ABDC có AB = AC ⇒ ABDC là hình thoi ⇒ AD ⊥ BC tại H.

+ H là trung điểm BC ⇒ BH = BC/2 = a/2.

+ ΔABH vuông tại H nên:

+ H là trung điểm AD ⇒ AD = 2. AH = a√3.

Câu 7:

Cho sáu điểm M, N, P, Q, R, S bất kỳ. Chứng minh rằng:

$\vec{M P} + \vec{N Q} + \vec{R S} = \vec{M S} + \vec{N P} + \vec{R Q}$

Xem đáp án

Áp dụng quy tắc ba điểm ta có:

Câu 8:

Cho tam giác OAB. Gọi M, N lần lượt là trung điểm của OA và OB. Tìm các số m, n sao cho:

a) $\vec{O M} = m . \vec{O A} + n . \vec{O B};$

b) $\vec{A N} = m . \vec{O A} + n . \vec{O B};$

c) $\vec{M N} = m . \vec{O A} + n . \vec{O B};$

d) $\vec{M B} = m . \vec{O A} + n . \vec{O B} .$

Xem đáp án

Câu 9:

Chứng minh rằng nếu G và G' lần lượt là trọng tâm của các tam giác ABC và A'B'C' thì $3 \vec{G G'} = \vec{A A'} + \vec{B B'} + \vec{C C'}$

Xem đáp án

+ G là trọng tâm ΔABC

Khi đó

Câu 10:

Trong mặt phẳng tọa độ Oxy, các khẳng định sau đúng hay sai?

a, Hai vectơ đối nhau thì chúng có hoành độ đối nhau.

b, Vectơ a→ ≠ 0→ cùng phương với vectơ i→ nếu a→ có hoành độ bằng 0.

c, Vectơ a→ có hoành độ bằng 0 thì cùng phương với vectơ j→

Xem đáp án

a) Đúng.

Hai vectơ đối nhau thì chúng có hoành độ đối nhau và tung độ đối nhau.

b) Sai.

Sửa lại: Vectơ a→ cùng phương với vectơ i→ nếu a→ có tung độ bằng 0.

c) Đúng.

Câu 11:

Cho $\vec{a} = (2; 1), \vec{b} = (3; - 4), \vec{c} = (- 7; 2)$

a) Tìm tọa độ của vectơ $\vec{u} = 3 . \vec{a} + 2 . \vec{b} - 4 . \vec{c}$ ;

b) Tìm tọa độ của vectơ $\vec{x}$ sao cho $\vec{x} + \vec{a} = \vec{b} - \vec{c}$ ;

c) Tìm các số k và h sao cho $\vec{c} = k . \vec{a} + h . \vec{b}$ .

Xem đáp án

Câu 12:

Cho $\vec{u} = \frac{1}{2} . \vec{i} - 5 . \vec{j}, \vec{v} = m . \vec{i} - 4 . \vec{j} .$ Tìm m để $\vec{u} v à \vec{v}$ cùng phương.

Xem đáp án

Câu 13:

Trong các khẳng định sau, khẳng định nào đúng?

a) Điểm A nằm trên trục hoành thì có hoành độ bằng 0.

b) P là trung điểm của đoạn thẳng AB khi và chỉ khi hoành độ của P bằng trung bình cộng các hoành độ của A và B.

c) Nếu tứ giác ABCD là hình bình hành thì trung bình cộng các tọa độ tương ứng của A và C bằng trung bình cộng các tọa độ tương ứng của B và D.

Xem đáp án

a) Sai

Sửa lại: Điểm A nằm trên trục hoành thì có tung độ bằng 0.

b) Sai

Ví dụ: A(2; 6), B(–4; 0) có trung bình cộng các hoành độ bằng –1.

P(–1; 3) là trung điểm của AB

P(–1; 2) không phải trung điểm của AB

P(–1; 0) không phải trung điểm của AB.

c) Đúng

ABCD là hình bình hành nên giao điểm O của AC và BD đồng thời là trung điểm của AC và BD

O là trung điểm của AC

O là trung điểm của BD

Câu 14:

Cho tứ giác ABCD. Số các vectơ khác 0→ có điểm đầu và điểm cuối là đỉnh của tứ giác bằng:

A. 4

B. 6

C. 8

D. 12

Xem đáp án

Chọn đáp án D. 12.

Các vectơ đó là:

Câu 15:

Cho lục giác đều ABCDEF có tâm O. Số các vectơ khác 0→ cùng phương với $\vec{O C}$ có điểm đầu và điểm cuối là đỉnh của lục giác bằng:

A. 4

B. 6

C. 7

D. 8

Xem đáp án

Chọn đáp án B. 6.

Các vectơ đó là:

Câu 16:

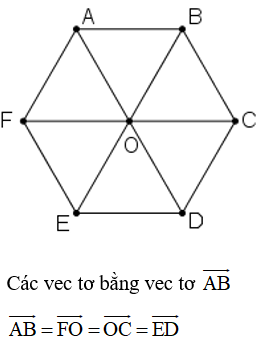
Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ $\vec{O C}$ có điểm đầu và điểm cuối là đỉnh của lục giác bằng:

A. 2

B. 3

C. 4

D. 6

Xem đáp án

Chọn đáp án A. 2.

Các vec tơ đó là

Câu 17:

Cho hình chữ nhật ABCD có AB = 3, BC = 4. Độ dài của vectơ $\vec{A C}$ là:

A. 5

B. 6

C. 7

D. 9

Xem đáp án

Chọn đáp án A. 5.

Giải thích :

Hình chữ nhật ABCD có AB = 3, BC = 4

Câu 18:

Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây là đúng?

A. $\vec{C A} + \vec{B A} = \vec{B C}$

B. $\vec{A B} + \vec{A C} = \vec{B C}$

C. $\vec{A B} + \vec{C A} = \vec{C B}$

D. $\vec{A B} - \vec{B C} = \vec{C A}$

Xem đáp án

Chọn đáp án C.

Giải thích:

Theo quy tắc ba điểm:

với D là đỉnh còn lại của hình bình hành ABDC.

với D là đỉnh còn lại của hình bình hành ABCD.

Câu 19:

Cho hai điểm phân biệt A và B. Điều kiện để điểm I là trung điểm của đoạn thẳng AB là:

A. IA = IB;

B. $\vec{I A} = \vec{I B};$

C. $\vec{I A} = - \vec{I B};$

D. $\vec{A I} = \vec{B I} .$

Xem đáp án

Chọn đáp án C.

Giải thích:

I là trung điểm của đoạn thẳng AB

Câu 20:

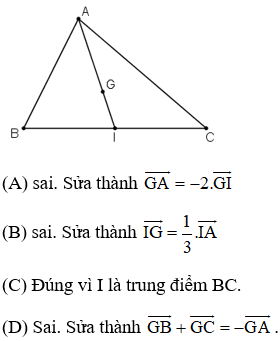
Cho tam giác ABC có G là trọng tâm, I là trung điểm của đoạn thẳng BC. Đẳng thức nào sau đây là đúng?

A. $\vec{G A} = 2 . \vec{G I}$

B. $\vec{I G} = \frac{- 1}{3} \vec{I A}$

C. $\vec{G B} + \vec{G C} = 2 . \vec{G I}$

D. $\vec{G B} + \vec{G C} = \vec{G A}$

Xem đáp án

Chọn đáp án C.

Câu 21:

Cho hình bình hành ABCD. Đẳng thức nào sau đây là đúng?

A. $\vec{A C} + \vec{B D} = 2 . \vec{B C}$

B. $\vec{A C} + \vec{B C} = \vec{A B}'$

C. $\vec{A C} - \vec{B D} = \vec{C D}$

D. $\vec{A C} - \vec{A D} = \vec{C D}$

Xem đáp án

Chọn A

Câu 22:

Trong mặt phẳng tọa độ Oxy cho hình bình hành OABC, C nằm trên Ox. Khẳng định nào sau đây là đúng?

A. $\vec{A B}$ có tung độ khác 0

B. A và B có tung độ khác nhau

C. C có hoành độ bằng 0

D. $x_{A} + x_{c} - x_{B} = 0$

Xem đáp án

Chọn đáp án D.

Giải thích:

C nằm trên Ox nên C(c; 0)

(A) sai:

ABCD là hình bình hành nên

Vậy có tung độ bằng 0.

(B) sai :

có tung độ bằng 0 nên y_B – y_A = 0 ⇒ y_A = y_B .

(C) sai vì C nằm trên Ox thì C có tung độ bằng 0.

(D) đúng:

Vì OABC là hình bình hành nên:

Câu 23:

Cho $\vec{u} = (3; - 2); \vec{v} = (1; 6)$

Khẳng định nào sau đây đúng?

A. $\vec{u} + \vec{v}$ và $\vec{a} = (- 4; 4)$ ngược hướng

B. $\vec{u}$ và $\vec{v}$ cùng phương

C. $\vec{u} - \vec{v}$ và $\vec{b} = (6; - 24)$ cùng hướng

D. $2 \vec{u} + \vec{v}$ và $\vec{v}$ cùng phương

Xem đáp án

Chọn đáp án C.

Câu 24:

Cho tam giác ABC có A(3; 5), B(1; 2), C(5; 2). Trọng tâm của tam giác ABC là:

A. $G_{1}$ (-3; 4)

B. $G_{2}$ (4; 0)

C. $G_{3}$ (√2; 3)

D. $G_{4}$ (3; 3)

Xem đáp án

Chọn đáp án D.

Trọng tâm tam giác ABC có tọa độ

Câu 25:

Cho bốn điểm A(1; 1), B(2; -1), C(4; 3), D(3; 5). Chọn mệnh đề đúng:

A. Tứ giác ABCD là hình bình hành

B. Điểm G(2 ; $\frac{5}{3}$ ) là trọng tâm của tam giác BCD

C. $\vec{A B} = \vec{C D}$

D. $\vec{A C}, \vec{A D}$ cùng phương

Xem đáp án

Chọn đáp án A.

Tứ giác ABCD là hình bình hành.

Giải thích :

Do A(1 ; 1) ; B(2 ; –1)

C(4 ; 3) ; D(3 ; 5)

Vậy nên ABCD là hình bình hành.

Câu 26:

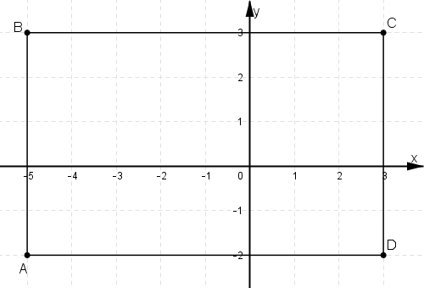
Trong mặt phẳng Oxy cho bốn điểm A(-5; -2), B(-5; 3), C(3; 3), D(3; -2). Khẳng định nào sau đây đúng:

A. $\vec{A B} v à \vec{C D}$ cùng hướng

B. Tứ giác ABCD là hình chữ nhật

C. Điểm I(-1;1) là trung điểm AC

D. $\vec{O A} + \vec{O B} = \vec{O C}$

Xem đáp án

Chọn đáp án B.

Tứ giác ABCD là hình chữ nhật.

Giải thích:

Câu 27:

Cho tam giác ABC. Đặt $\vec{a} = \vec{B C}, \vec{b} = \vec{A C}$

Các cặp vectơ nào cùng phương?

A. $2 \vec{a} + \vec{b} v à \vec{a} + 2 \vec{b}$

B. $\vec{a} - 2 \vec{b} v à 2 \vec{a} - \vec{b}$

C. $5 \vec{a} + \vec{b} v à - 10 \vec{a} - 2 \vec{b}$

D. $\vec{a} + \vec{b} v à \vec{a} - \vec{b}$

Xem đáp án

Chọn đáp án C.

Giải thích:

Câu 28:

Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ. Khẳng định nào sau đây là đúng?

A. $|\vec{O A} + \vec{O B}| = A B$

B. $\vec{O A} - \vec{O B} v à \vec{D C}$ cùng hướng

C. $x_{A} = - x_{C} v à y_{A} = y_{C}$

D. $x_{B} = - x_{C} v à y_{C} = - y_{B}$

Xem đáp án

Chọn đáp án A.

Giải thích:

Câu 29:

Cho M(3; -4). Kẻ MM₁ vuông góc với Ox, MM₂ vuông góc với Oy. Khẳng định nào sau đây là đúng?

A. $O M_{1} = - 3$

B. $O M_{2} = 4$

C. $O M_{1} - O M_{2}$ có tọa độ (-3;-4)

D. $O M_{1} + O M_{2}$ có tọa độ (3; -4)

Xem đáp án

Chọn đáp án D.

Giải thích :

Câu 30:

Trong mặt phẳng tọa độ Oxy cho A(2; -3), B(4; 7). Tọa độ trung điểm I của đoạn thẳng AB là:

A. (6; 4)

B. (2; 10)

C. (3; 2)

D. (8; -21)

Xem đáp án

Chọn đáp án C. (3; 2)

Giải thích:

Điểm A(2; –3) ; B(4; 7), trung điểm I có tọa độ là hay I(3; 2).

Câu 31:

Trong mặt phẳng tọa độ Oxy cho A(5; 2), B(10; 8). Tọa độ vectơ $\vec{A B}$ là:

A. (15; 10)

B. (2; 4)

C. (5; 6)

D. (50; 16)

Xem đáp án

Chọn đáp án C. (5; 6).

Giải thích:

Câu 32:

Trong tam giác ABC có B(9; 7), C(11; -1), M và N lần lượt là trung điểm của AB và AC. Tọa độ của vectơ $\vec{M N}$ là:

A. (2; -8)

B. (1; -4)

C. (10; 6)

D. (5; 3)

Xem đáp án

Chọn đáp án B. (1 ; –4).

Giải thích:

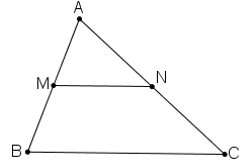
M là trung điểm AB, N là trung điểm AC nên MN là đường trung bình của ΔABC.

⇒ MN // BC nên cùng hướng với

Mà MN = 1/2 . BC nên

B(9 ; 7), C(11 ; –1)

Câu 33:

Trong mặt phẳng tọa độ Oxy cho bốn điểm: A(3; 2), B(7; 1), C(0; 1), D(-8; -5).

Khẳng định nào sau đây là đúng?

A. $\vec{A B} v à \vec{C D}$ đối nhau

B. $\vec{A B} v à \vec{C D}$ cùng phương nhưng ngược hướng

C. $\vec{A B} v à \vec{C D}$ cùng phương và cùng hướng

D. A, B, C, D thuộc cùng một đường thẳng

Xem đáp án

Chọn đáp án B.

Giải thích:

Vậy nên và cùng phương nhưng ngược hướng.

Câu 34:

Cho ba điểm A(-1; 5), B(5; 5), C(-1; 11). Khẳng định nào sau đây là đúng?

A. A, B, C thẳng hàng

B. $\vec{A B} v à \vec{A C}$ thẳng hàng

C. $\vec{A B} v à \vec{A C}$ không cùng phương

D. $\vec{A C} v à \vec{B C}$ cùng phương

Xem đáp án

Chọn đáp án C.

Giải thích:

Câu 35:

Cho $\vec{a} = (3; - 4), \vec{b} = (- 1; 2)$ . Tọa độ của vectơ $\vec{a} + \vec{b}$ là:

A. (-4; 6)

B. (2; -2)

C. (4; -6)

D. (-3; -8)

Xem đáp án

Chọn đáp án B.

Câu 36:

Cho $\vec{a} = (- 1; 2), \vec{b} = (5; - 7)$ . Tọa độ của vectơ $\vec{a} - \vec{b}$ là:

A. (-4; 6)

B. (2; -2)

C. (-6; 9)

D. (-3; -8)

Xem đáp án

Chọn đáp án C. (–6; 9)

Giải thích

Câu 37:

Cho $\vec{a} = (- 5; 0), \vec{b} = (4; x)$ . Hai vectơ a→ và b→ cùng phương nếu số x là:

A. -5

B. 4

C. 0

D. -1

Xem đáp án

Chọn đáp án C.

Giải thích:

a→ (-5; 0) cùng phương với i→

b→ cùng phương với a→ ⇔ b→ cùng phương với i→ ⇔ b→ (4; 0).

Câu 38:

Cho $\vec{a} = (x; 2), \vec{b} = (- 5; 1), \vec{c} = (x; 7)$ , vectơ $\vec{c} = 2 \vec{a} + 3 \vec{b}$ nếu:

A. x = -15

B. x = 3

C. x = 15

D. x = 5

Xem đáp án

Chọn đáp án C. x = 15

Giải thích:

Câu 39:

Cho A(1; 1), B(-2; -2), C(7; 7). Khẳng định nào đúng?

A. G(2; 2) là trọng tâm tam giác ABC

B. Điểm B ở giữa hai điểm A và C

C. Điểm A ở giữa hai điểm B và C

D. Hai vec tơ $\vec{A B}, \vec{A C}$ cùng hướng

Xem đáp án

Chọn đáp án C. Điểm A ở giữa hai điểm B và C

Giải thích :

nên hai vec tơ cùng phương ⇒ A, B, C thẳng hàng.

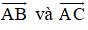
+ (A) sai vì A, B, C thẳng hàng nên ΔABC không tồn tại.

+ (B) sai vì x_B < x_A < x_C nên A nằm giữa B và C.

+ (C) đúng

+ (D) sai vì -2 < 0 nên 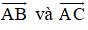ngược hướng.a

Câu 40:

Các điểm M(2; 3), N(0; -4), P(-1; 6) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC. Tọa độ đỉnh A của tam giác là:

A. (1; 5)

B. (-3; -1)

C. (-2; -7)

D. (1; -10)

Xem đáp án

Chọn đáp án B. (–3 ; –1)

Giải thích:

M là trung điểm BC nên ta có:

N là trung điểm CA nên ta có:

P là trung điểm của AB nên ta có

Giải hệ phương trình 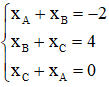ta được x_A = -3

Giải hệ phương trình 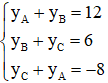ta được y_A = -1

Vậy A(–3 ; –1).

Câu 41:

Cho tam giác ABC có gốc tọa độ O là trọng tâm, A(-2; 2), B(3; 5). Tọa độ của đỉnh C là:

A. (-1; -7)

B. (2; -2)

C. (-3; -5)

D. (1; 7)

Xem đáp án

Chọn đáp án A. (–1 ; –7)

Giải thích:

O là trọng tâm tam giác ABC

Vậy C(–1 ; –7)

Câu 42:

Khẳng định nào trong các khẳng định sau đây là đúng?

A. Hai vectơ $\vec{a} = (- 5; 0), \vec{b} = (- 4; 0)$ cùng hướng

B. Vectơ $\vec{c} = (7; 3)$ là vectơ đối của $\vec{d} = (- 7; 3)$

C. Hai vectơ $\vec{u} = (4; 2), \vec{v} = (8; 3)$ cùng phương

D. Hai vectơ $\vec{a} = (6; 3), \vec{b} = (2; 1)$ ngược hướng

Xem đáp án

Chọn đáp án A. Hai vectơ và cùng hướng.

Giải thích :

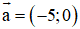
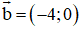
(A) đúng vì và đều ngược hướng với i→ nên a→ và b→ cùng hướng.

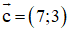
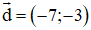
(B) Sai. Vec tơ đối của là vec tơ .

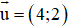
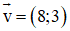
(C) Sai. và không cùng phương vì giả sử u→ và v→ cùng phương thì tồn tại k để

(D) Sai. Vì a→ = 3b→ nên a→ và b→ cùng hướng.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SGK Toán 10 Chương 1: Vectơ

Ôn tập chương 1

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương