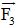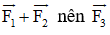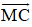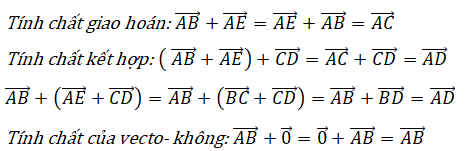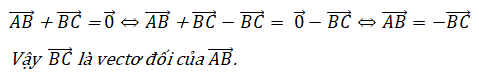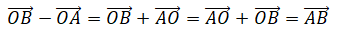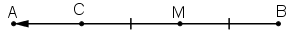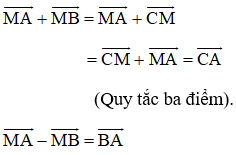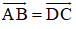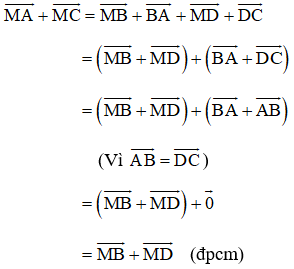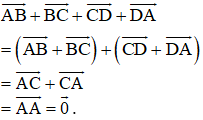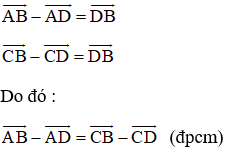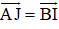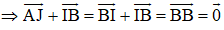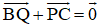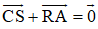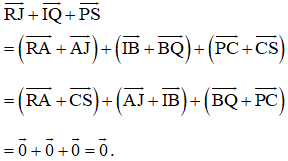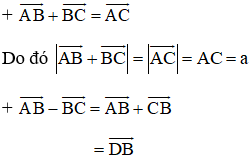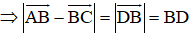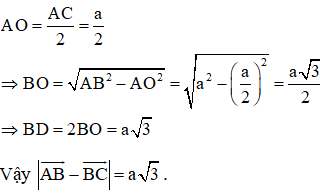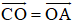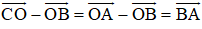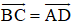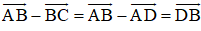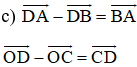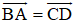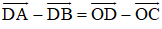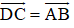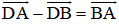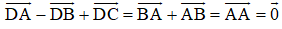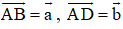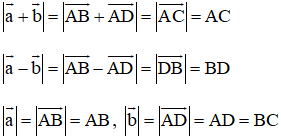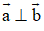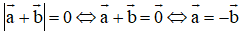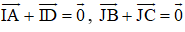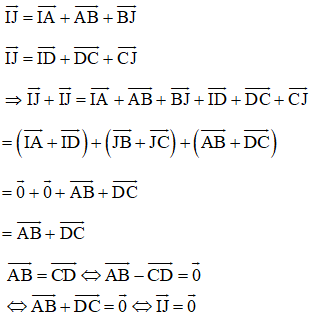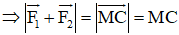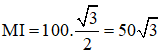Bài 2: Tổng và hiệu của hai vectơ
-
2556 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
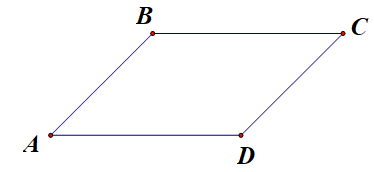
Vẽ hình bình hành ABCD. Hãy nhận xét về độ dài và hướng của hai vectơ AB→ và CD→.
 Xem đáp án
Xem đáp án
Về độ dài: hai vectơ AB→ và CD→ có cùng độ dài
Về hướng: hai vectơ AB→ và CD→ có hướng ngược nhau.
Câu 5:
Cho đoạn thẳng AB và điểm M nằm giữa A và B sao cho AM > MB. Vẽ các vectơ
 Xem đáp án
Xem đáp án
– Trên đoạn MA, lấy điểm C sao cho MC = MB
Nhận thấy 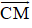
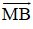
Khi đó:
Câu 6:
Cho hình bình hành ABCD và điểm M tùy ý. Chứng minh rằng
 Xem đáp án
Xem đáp án
Ta có: ABCD là hình bình hành nên
Câu 7:
Chứng minh rằng đối với tứ giác ABCD bất kỳ ta luôn có:
a)
b)
 Xem đáp án
Xem đáp án
a) Ta có:
b) Áp dụng quy tắc trừ hai vec tơ ta có:
Câu 8:
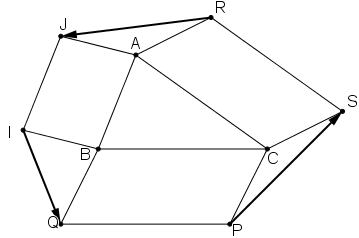
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành: ABIJ, BCPQ, CARS. Chứng minh rằng
 Xem đáp án
Xem đáp án
Ta có:
AJIB là hình bình hành nên
Tương tự như vậy:
BCPQ là hình bình hành nên
CARS là hình bình hành nên
Do đó:
Câu 9:
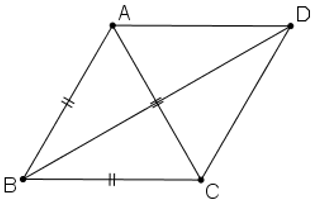
Cho tam giác đều ABC cạnh bằng a. Tính độ dài của các vectơ
 Xem đáp án
Xem đáp án
Ta có:
(Quy tắc hình bình hành)
(Trong đó D là đỉnh còn lại của hình bình hành ABCD)
+ Tính BD:
Hình bình hành ABCD có AB = BC = a nên ABCD là hình thoi.
⇒ AC ⊥ BD tại O là trung điểm của AC và BD.
Câu 10:
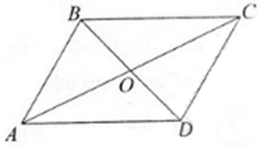
Cho hình bình hành ABCD có tâm O. Chứng minh rằng:
a)
b)
c)
d)
 Xem đáp án
Xem đáp án
a) Ta có:
O là trung điểm của AC nên
Do đó
b) ABCD là hình bình hành nên
Do đó
Mà ABCD là hình bình hành nên
Do đó
d) ABCD là hình bình hành nên
Lại có
Do đó
Câu 11:
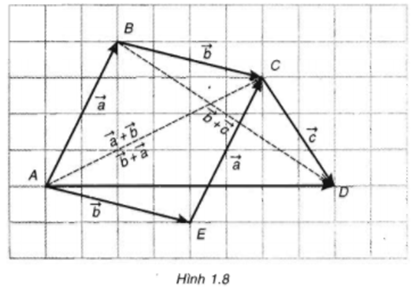
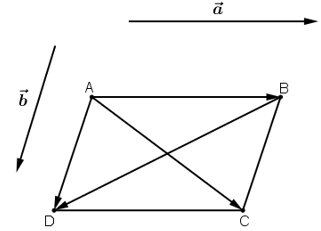
Cho vectơ a, b là hai vectơ khác vectơ 0. Khi nào có đẳng thức
a)
b)
 Xem đáp án
Xem đáp án
Có hai vec tơ a→, b→ bất kì như hình vẽ.
Vẽ hình bình hành ABCD sao cho
Ta có:
Do đó
a) 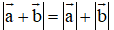
b) 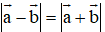
Câu 12:
Cho |a→ + b→| = 0. So sánh độ dài, phương và hướng của hai vectơ a→ và b→.
 Xem đáp án
Xem đáp án
⇔ a→ và b→ là hai vec tơ đối nhau
⇔ a→ và b→ cùng phương, ngược hướng và có cùng độ dài.
Câu 13:
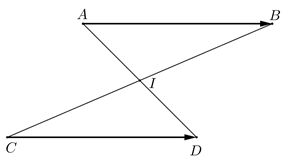
Chứng minh rằng khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau.
 Xem đáp án
Xem đáp án
Gọi trung điểm của AD là I, trung điểm BC là J.
Khi đó ta có:
Mà theo quy tắc ba điểm ta có:
⇔ I ≡ J hay trung điểm AD và BC trùng nhau (đpcm)
Câu 14:
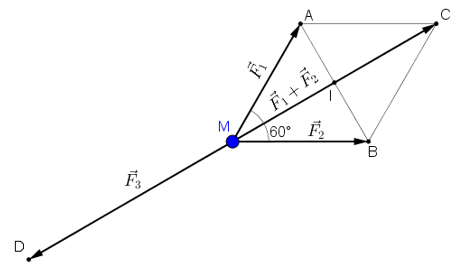
Cho ba lực cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của hai lực F1, F2 đều là 100N và = 60o. Tìm cường độ và hướng của lực F3.
 Xem đáp án
Xem đáp án
Ta biểu diễn 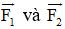
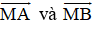
Khi đó 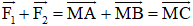
+ Tính MC : Gọi I là trung điểm của AB ⇒ I là trung điểm của MC.
Δ MAB có MA = MB = 100 và góc AMB = 60º nên là tam giác đều
⇒ đường cao
⇒ MC = 2.MI = 100√3.
Vec tơ