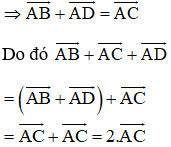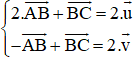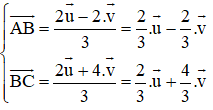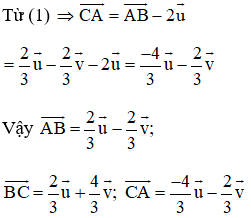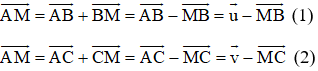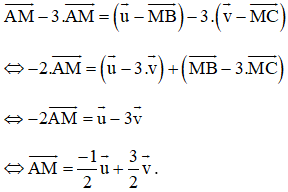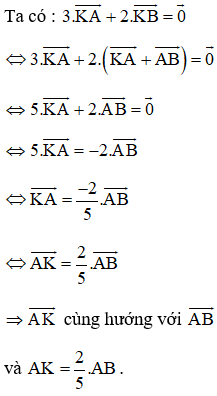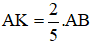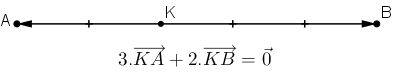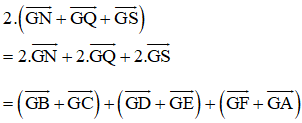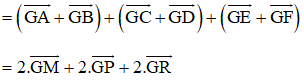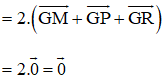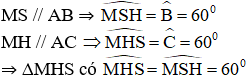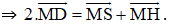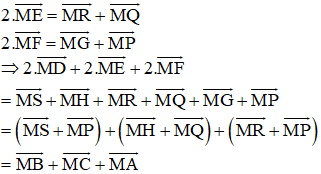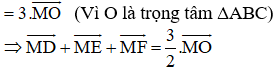Bài 3: Tích của vectơ với một số
-
2398 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
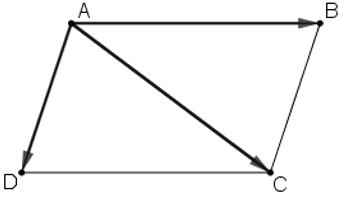
Cho vectơ a→ ≠ 0→. Xác định độ dài và hướng của vectơ a→ + a→.
Xem đáp án
Ta có: a→ + a→ = 2a→
Độ dài của vectơ a→ + a→ bằng 2 lần độ dài của vectơ a→
Hướng của vectơ a→ + a→ cùng hướng với vectơ a→
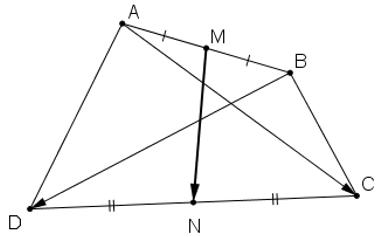
Câu 3:
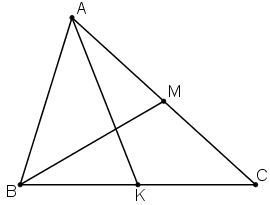
Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ theo hai vectơ
Xem đáp án
+ K là trung điểm của BC nên ta có:
+ M là trung điểm AC nên ta có:
+ Lại có 
Cộng (1) với (3) ta được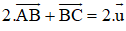 
, kết hợp với (2) ta được hệ phương trình: 
Giải hệ phương trình ta được 
Câu 4:
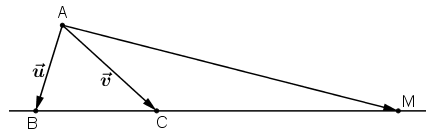
Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho . Hãy phân tích vectơ theo hai vectơ
Xem đáp án
Ta có: 
Theo quy tắc ba điểm ta có:
Lấy (1) trừ 3 lần (2) ta được:
Câu 7:
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho
Xem đáp án
hay K là điểm nằm trên đoạn thẳng AB và 
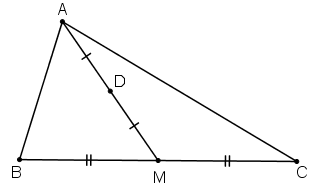
Câu 8:
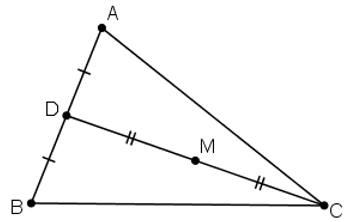
Cho tam giác ABC. Tìm điểm M sao cho
Xem đáp án
Gọi D là trung điểm AB.
Khi đó với mọi điểm M ta có :
⇔ M là trung điểm của trung tuyến từ đỉnh C.
Câu 9:
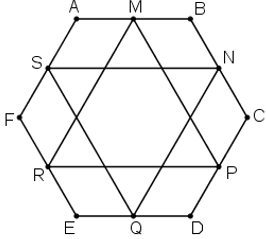
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Xem đáp án
Gọi G là trọng tâm tam giác MPR 
Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh 
Thật vậy ta có:
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)
(Vì M, P, R là trung điểm AB, CD, EF)
hay G cũng là trọng tâm của ΔNQS.
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.
Câu 10:
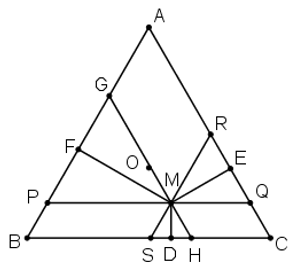
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.
Chứng minh rằng
Xem đáp án
Ta có:
⇒ ΔMHS đều.
MD ⊥ SH nên MD là đường cao đồng thời là trung tuyến của ΔMHS.
⇒ D là trung điểm của HS
Chứng minh tương tự ta có:
(Vì các tứ giác BSMP, HMQC, MRAG là hình bình hành)
