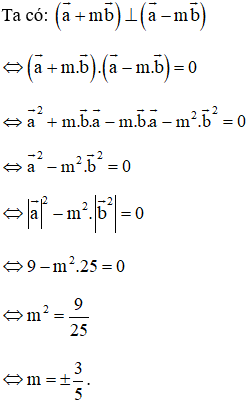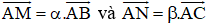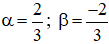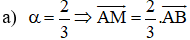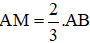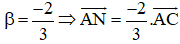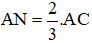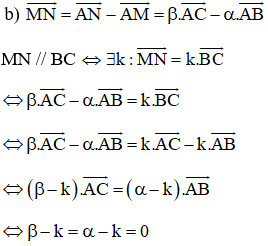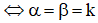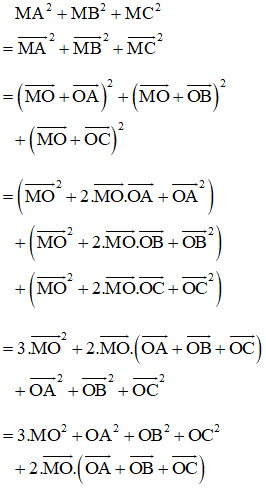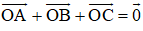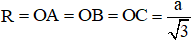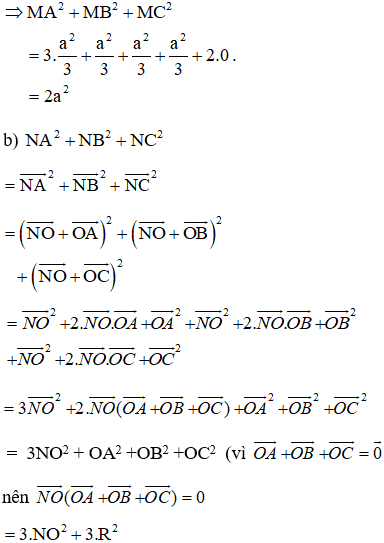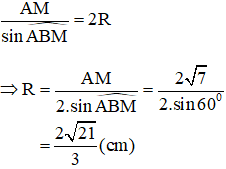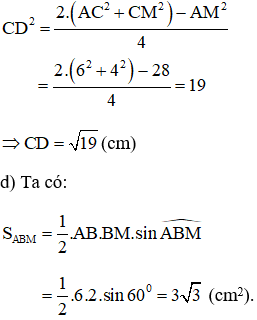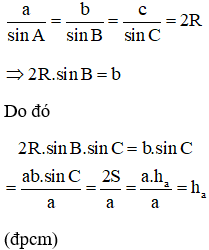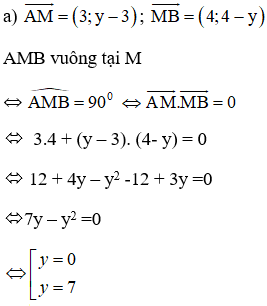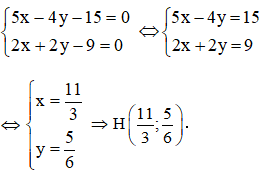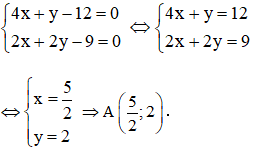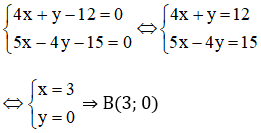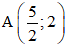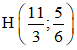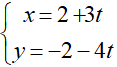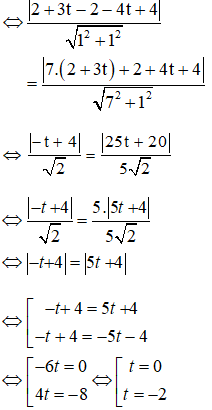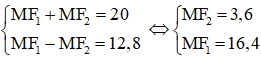Ôn tập cuối năm hình học 10
-
2217 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
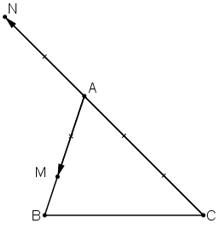
Cho tam giác ABC và hai điểm M, N sao cho
a) Hãy vẽ M, N khi
b) Tìm mối liên hệ giữa α và β để MN song song với BC.
 Xem đáp án
Xem đáp án
Vậy 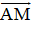
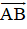
và có độ dài
Vậy 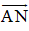
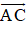
và có độ dài
(Do hai vec tơ 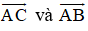
nên chỉ bằng nhau khi chúng đồng thời bằng 0→).
Vậy MN song song với BC khi và chỉ khi α = β.
Câu 3:
Cho tam giác đều ABC cạnh a.
a, Cho M là một điểm trên đường tròn ngoại tiếp tam giác ABC. Tính MA2 + MB2 + MC2 theo a.
b, Cho đường thẳng d tùy ý, tìm điểm N trên đường thẳng d sao cho NA2 + NB2 + NC2 nhỏ nhất.
 Xem đáp án
Xem đáp án
a) Gọi O là tâm đường tròn ngoại tiếp.
Do tam giác ABC là tam giác đều
nên O đồng thời là trọng tâm tam giác đều ABC.
Lại có:
+ O là trọng tâm tam giác nên
+ Bán kính đường tròn ngoại tiếp tam giác:
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.
Câu 4:
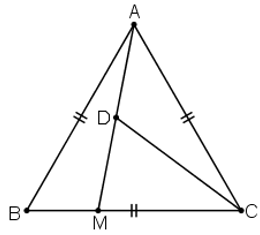
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
 Xem đáp án
Xem đáp án
a) Do tam giác ABC là tam giác đều nên 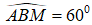
Theo định lý côsin trong tam giác ABM ta có:
b) Theo định lý sin trong tam giác ABM ta có:
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
Câu 5:
Chứng minh rằng trong mọi tam giác ABC ta đều có:
a, a = b cosC + c cosB;
b, sinA = sinBcosC + sinCcosB;
c, ha = 2RsinBsinC.
 Xem đáp án
Xem đáp án
a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
Câu 6:
Cho các điểm A(2; 3), B(9; 4), M(5; y) và P(x; 2).
a, Tìm y để tam giác AMB vuông tại M;
b, Tìm x để ba điểm A, B và P thẳng hàng.
 Xem đáp án
Xem đáp án
Vậy với M(5; 7) hoặc M(5; 0) thì tam giác ABM vuông tại M.
Vậy P(-5; 2)
Câu 7:
Cho tam giác ABC với H là trực tâm. Biết phương trình đường thẳng AB, BH và AH lần lượt là 4x + y – 12 = 0, 5x – 4y – 15 = 0 và 2x + 2y – 9 = 0. Hãy viết phương trình hai đường thẳng chứa hai cạnh còn lại và đường cao thứ ba.
 Xem đáp án
Xem đáp án
Trực tâm H là giao điểm của BH và AH
⇒ tọa độ H là nghiệm của hệ:
A là giao điểm của AB và AH
nên tọa độ A là nghiệm của hệ phương trình:
B là giao điểm BH và AB
nên tọa độ điểm B là nghiệm của hệ:
+ AC ⊥ HB, mà HB có một vtpt là
(5; -4)⇒ AC nhận (4; 5) là một vtpt
AC đi qua
⇒ Phương trình đường thẳng
AC: 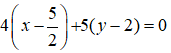
+ CH ⊥ AB, AB có một vtpt là (4; 1)
⇒ CH nhận (1; -4) là một vtpt
CH đi qua
⇒ Phương trình đường thẳng
CH: 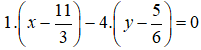
+ BC ⊥ AH , mà AH nhận (2; 2) là một vtpt
⇒ BC nhận (1; -1) là một vtpt
BC đi qua B(3; 0)
⇒ Phương trình đường thẳng
BC: 1(x - 3) – 1(y – 0) = 0 hay x – y – 3 = 0.
Câu 8:
Lập phương trình đường tròn có tâm nằm trên đường thẳng Δ: 4x + 3y – 2 = 0 và tiếp xúc với hai đường thẳng d1: x + y + 4 = 0 và d2: 7x – y + 4 = 0.
 Xem đáp án
Xem đáp án
Giả sử đường tròn cần lập có tâm O; bán kính R.
Đường thẳng Δ đi qua M(2; -2) và có VTPT là
n→(4; 3) nên đường thẳng này có 1 VTCP là u→(3; -4)
Phương trình tham số của đường thẳng Δ là:
O nằm trên Δ ⇒ O(2 + 3t; -2 – 4t)
Đường tròn (O; R) tiếp xúc với d1 và d2
⇒ d(O; d1) = d(O; d2) = R
Ta có: d(O; d1) = d(O; d2)
+ Với t = 0 ⇒ O(2; -2) ⇒ R = d(O; d1) = 2√2
Phương trình đường tròn: (x – 2)2 + (y + 2)2 = 8.
+ Với t = -2 ⇒ O(-4; 6) , R = d(O; d1) = 3√2
Phương trình đường tròn: (x + 4)2 + (y – 6)2 = 18
Vậy có hai phương trình đường tròn thỏa mãn là:
(x – 2)2 + (y + 2)2 = 8 hoặc (x + 4)2 + (y – 6)2 = 18
Câu 9:
Cho elip (E) có phương trình:
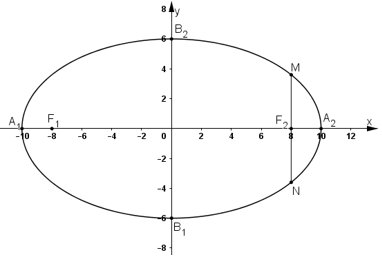
a, Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip (E) và vẽ elip đó.
b, Qua tiêu điểm của elip dựng đường song song với Oy và cắt elip tại hai điểm M và N. Tính độ dài đoạn MN.
 Xem đáp án
Xem đáp án
a) (E): 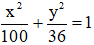
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
Vậy MN = 2.MF2 = 7,2.

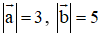 ,
, 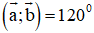 . Với giá trị nào của m thì hai vec tơ
. Với giá trị nào của m thì hai vec tơ 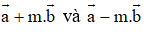 vuông góc với nhau?
vuông góc với nhau?