15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hàm số bậc hai có đáp án (Nhận biết)

Câu 1:

Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol $y = - 2 x^{2} + 5 x + 3$

A. $x = \frac{5}{2}$

B. $x = - \frac{5}{2}$

C. $x = \frac{5}{4}$

D. $x = - \frac{5}{4}$

Xem đáp án

Đáp án cần chọn là: C

Ta có:

$\frac{- b}{2 a} = \frac{- 5}{2. (- 2)} = \frac{5}{4}$

Trục đối xứng là đường thẳng: $x = \frac{5}{4}$

Câu 2:

Trong các hàm số sau, hàm số nào có đồ thị nhận đường x = 1 làm trục đối xứng?

A. y = −2x²+ 4x + 1

B. y = 2x²+ 4x − 3

C. y = 2x²− 2x − 1

D. y = x²– x + 2

Xem đáp án

Đáp án cần chọn là: A

Xét đáp án A, ta có $- \frac{b}{2 a} = 1$

Câu 3:

Đỉnh I của parabol (P): y= –3x²+ 6x – 1 là:

A. I (1; 2)

B. I (3; 0)

C. I (2 ;−1)

D. I (0; −1)

Xem đáp án

Đáp án cần chọn là: A

Ta có:

$\frac{- b}{2 a} = \frac{- 6}{2. (- 3)} = \frac{- 6}{- 6} = 1$

$\frac{- Δ}{4 a} = \frac{- (b^{2} - 4 a c)}{4 a} = \frac{- 6^{2} + 4. (- 3) . (- 1)}{4. (- 3)} = \frac{- 36 + 12}{- 12} = \frac{- 24}{- 12} = 2$

Suy ra đỉnh của Parabol là: I (1; 2)

Câu 4:

Hàm số nào sau đây có đồ thị là parabol có đỉnh I (−1; 3)?

A. y = 2x²− 4x − 3

B. y = 2x²−2x − 1

C. y = 2x²+ 4x + 5

D. y = 2x²+ x + 2

Xem đáp án

Đáp án cần chọn là: C

Đáp án A: Hoành độ đỉnh $x = - \frac{- 4}{2.2} = 1$ nên loại

Đáp án B: Hoành độ đỉnh $x = - \frac{- 2}{2.2} = \frac{1}{2}$ nên loại

Đáp án C: Hoành độ đỉnh $x = - \frac{4}{2.2} = - 1 \Rightarrow y = 2. {(- 1)}^{2} + 4. (- 1) + 5 = 3$ hay đỉnh (-1; 3)

Đáp án D: Hoành độ đỉnh $x = - \frac{1}{2.2} = - \frac{1}{4}$ nên loại

Câu 5:

Biết parabol (P): y = ax²+ 2x + 5 đi qua điểm A (2; 1). Giá trị của a là:

A. a = –5

B. a = –2

C. a = 2

D. Một đáp số khác

Xem đáp án

Đáp án cần chọn là: B

Parabol đi qua điểm A (2; 1) nên ta có: 4a + 4 +5 = 1 $\Leftrightarrow$ 4a = -8 $\Leftrightarrow$ a = -2

Câu 6:

Tìm parabol (P): y = ax² + 3x − 2, biết rằng parabol cắt trục Ox tại điểm có hoành độ bằng 2.

A. y = x²+ 3x − 2

B. y = −x²+ x − 2

C. y = −x²+ 3x − 3

D. y = −x²+ 3x − 2

Xem đáp án

Đáp án cần chọn là: D

Vì (P) cắt trục Ox tại điểm có hoành độ bằng 2 nên điểm A (2; 0) thuộc (P).

Thay $\{\begin{matrix} x = 2 \\ y = 0 \end{matrix}$ vào (P), ta được 0 = 4a + 6 – 2 ⇔ a = −1.

Vậy (P): y = −x²+ 3x − 2.

Câu 7:

Đỉnh của parabol $y = x^{2} + x + m$ nằm trên đường thẳng $y = \frac{3}{4}$ nếu m bằng:

A. Một số tùy ý

B. 3

C. 5

D. 1

Xem đáp án

Đáp án cần chọn là: D

Yêu cầu bài toán $\Leftrightarrow \frac{- b^{2} + 4 a c}{4 a} = \frac{3}{4} \Leftrightarrow \frac{- 1 + 4 m}{4} = \frac{3}{4} \Leftrightarrow 4 m = 4 \Leftrightarrow m = 1$

Câu 8:

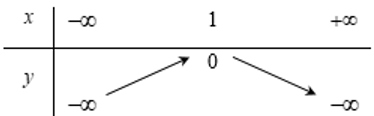
Bảng biến thiên của hàm số y = -x² + 2x – 1 là:

A. VietJack

B. VietJack

C. VietJack

D. VietJack

Xem đáp án

Đáp án cần chọn là: C

Ta có:

$a = - 1 < 0; \frac{- b}{2 a} = \frac{- 2}{2. (- 1)} = \frac{- 2}{- 2} = 1$

$y (1) = - 1^{2} + 2.1 - 1 = 0$

Suy ra bảng biến thiên:

Câu 9:

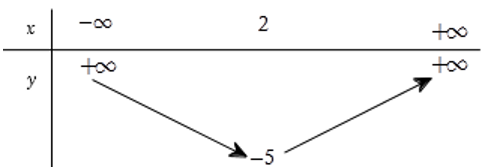
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?

A. y = −x²+ 4x − 9

B. y = x²− 4x − 1

C. y = −x²+ 4x

D. y = x²− 4x − 5

Xem đáp án

Đáp án cần chọn là: B

Nhận xét:

Bảng biến thiên có bề lõm hướng lên. Loại đáp án A và C.

Đỉnh của parabol có tọa độ là (2; −5). Xét các đáp án còn lại, đáp án B thỏa mãn.

Câu 10:

Bảng biến thiên của hàm số y = −2x²+ 4x + 1 là bảng nào trong các bảng được cho sau đây?

A. VietJack

B. VietJack

C. VietJack

D. VietJack

Xem đáp án

Đáp án cần chọn là: C

Hệ số a = -2 < 0 suy ra bề lõm hướng xuống. Loại B, D

Ta có $- \frac{b}{2 a} = 1$ và y(1) = 3. Do đó C thỏa mãn

Câu 11:

Hàm số y = 2x²+ 4x – 1

A. Đồng biến trên khoảng (−∞; −2) và nghịch biến trên khoảng (−2; +∞).

B. Nghịch biến trên khoảng (−∞; −2) và đồng biến trên khoảng (−2; +∞).

C. Đồng biến trên khoảng (−∞; −1) và nghịch biến trên khoảng (−1; +∞).

D. Nghịch biến trên khoảng (−∞; −1) và đồng biến trên khoảng (−1; +∞).

Xem đáp án

Đáp án cần chọn là: D

Ta có: $- \frac{b}{2 a} = - 1$ . Do đó hàm số nghịch biến trên khoảng $(- \infty; - 1)$ và đồng biến trên khoảng $(- 1; + \infty)$

Câu 12:

Hàm số nào sau đây nghịch biến trong khoảng ( $- 1; + \infty$ )?

A. $y = \sqrt{2} x^{2} + 1$

B. $y = - \sqrt{2} x^{2} + 1$

C. $y = \sqrt{2} {(x + 1)}^{2}$

D. $y = - \sqrt{2} {(x + 1)}^{2}$

Xem đáp án

Đáp án cần chọn là: D

Xét đáp án D, ta có $y = - \sqrt{2} {(x + 1)}^{2} = - \sqrt{2} x^{2} - 2 \sqrt{2} x - \sqrt{2}$ nên $- \frac{b}{2 a} = - 1$ và có a < 0 nên hàm số đồng biến trên khoảng $(- \infty; - 1)$ và nghịch biến trên khoảng $(- 1; + \infty)$

Câu 13:

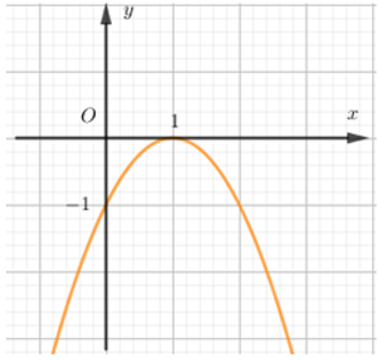
Hình vẽ bên là đồ thị của hàm số nào?

A. y = −(x + 1)²

B. y = −(x − 1)²

C. y = (x + 1)²

D. y = (x − 1)²

Xem đáp án

Đáp án cần chọn là: B

- Đồ thị hàm số đi qua điểm (1; 0) nên loại A và C.

- Bề lõm hướng xuống dưới nên a < 0.

Câu 14:

Cho đồ thị hàm số y = ax²+ bx + c như hình vẽ.

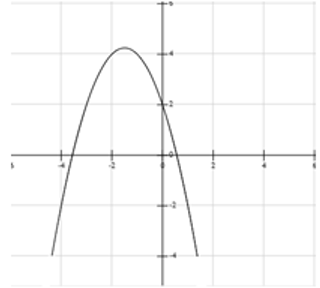
Khẳng định nào sau đây là đúng:

A. a > 0, b < 0, c > 0

B. a < 0, b > 0, c > 0

C. a < 0, b < 0, c < 0

D. a < 0, b < 0, c > 0

Xem đáp án

Đáp án cần chọn là: D

Bề lõm của đồ thị quay xuống dưới nên hệ số a < 0.

Giao điểm của đồ thị hàm số với trục tung nằm trên trục có tung độ dương nên c > 0

Hoành độ đỉnh x = $- \frac{b}{2 a}$ < 0. Mà a < 0 nên b < 0.

Câu 15:

Giao điểm của parabol (P): y = x²+ 5x + 4 với trục hoành:

A. (−1; 0); (−4; 0)

B. (0; −1); (0; −4).

C. (−1; 0); (0; −4).

D. (0; −1); (−4; 0)

Xem đáp án

Đáp án cần chọn là: A

- Xét phương trình hoành độ giao điểm: x² + 5x + 4 = 0

- Phương trình có hai nghiệm x₁ = -1; x₂ = -4 nên các giao điểm là

(-1; 0), (-4; 0)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Hàm số bậc hai có đáp án

Trắc nghiệm Hàm số bậc hai có đáp án (Nhận biết)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương