Trắc nghiệm Hàm số bậc hai có đáp án (Vận dụng)
-
4659 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số y = −x2 + 2x + 1. Gọi M và m là giá trị lớn nhất vá giá trị nhỏ nhất của hàm số trên [0; 2].
Tính giá trị của biểu thức T = M2 + m2
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Hàm số y = −x2 + 2x + 1 có a = −1 < 0; ⇒ Hàm số đồng biến trên (−∞;1) và nghịch biến trên (1;+∞).
BBT
: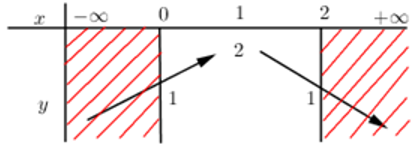
Dựa vào BBT ta thấy M = 2 và m = 1 ⇒ T = M2 + m2 = 22 +12 = 5.
Câu 2:
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Hàm số có a = 1 > 0 nên bề lõm hướng lên
Hoành độ đỉnh
Vậy
Câu 4:
Tìm giá trị thực của hàm số y = mx2 -2mx – 3m – 2 có giá trị nhỏ nhất bằng -10 trên R
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Ta có suy ra y = -4m – 2
Hàm số có giá trị nhỏ nhất bằng – 10
Câu 5:
Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số trên đoạn bằng 3. Tính tổng T các phần tử của S
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Parabol có hệ số theo x2 là 4 > 0 nên bề lõm hướng lên. Hoành độ đỉnh xI = .
Nếu < −2 ⇔ m < −4 thì xI < − 2 < 0. Suy ra f(x) đồng biến trên đoạn [−2; 0].
Do đó f(x) = f(−2) = m2 + 6m + 16.
Theo yêu cầu bài toán: m2 + 6m + 16 = 3 (vô nghiệm).
Nếu −2 ≤ ≤ 0 ⇔ −4 ≤ m ≤ 0 thì xI ∈ [0; 2].
Suy ra f(x) đạt giá trị nhỏ nhất tại đỉnh. Do đó f(x) = f() = −2m.
Theo yêu cầu bài toán −2m = 3 ⇔ m = − (thỏa mãn −4 ≤ m ≤ 0).
Nếu > 0 ⇔ m > 0 thì xI > 0 > −2. Suy ra f(x) nghịch biến trên đoạn [−2; 0].
Do đó f(x) = f(0) = m2 – 2m.
Theo yêu cầu bài toán: m2 − 2m = 3 ⇔
Bảng biến thiên:
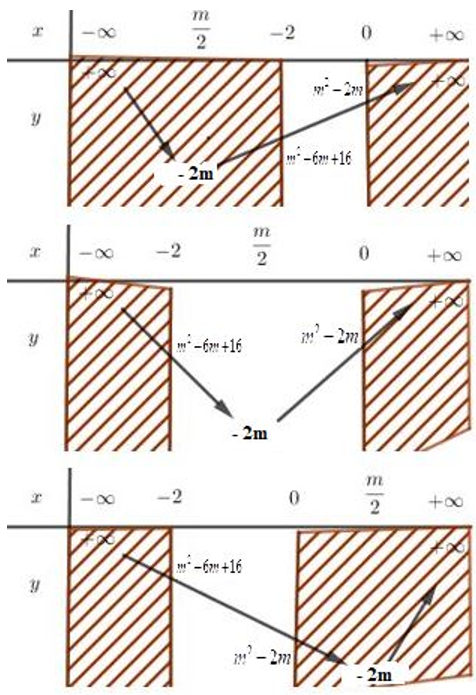
Vậy T =
Câu 6:
Cho hàm số y = ax2 + bx + c có đồ thị như hình bên. Khẳng định nào sau đây đúng?
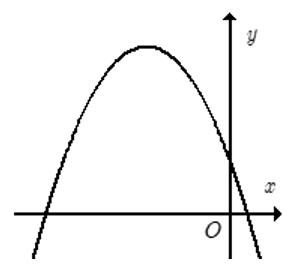
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Bề lõm hướng xuống nên a < 0.
Hoành độ đỉnh parabol x = -< 0 nên b < 0.
Parabol cắt trục tung tại điểm có tung độ dương nên c > 0.
Câu 7:
Xác định parabol (P): y = ax2 + bx + c, biết rằng (P) cắt trục Ox tại hai điểm có hoành độ lần lượt là −1 và 2, cắt trục Oy tại điểm có tung độ bằng −2.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Gọi A và B là hai giao điểm cuả (P) với trục Ox có hoành độ lần lượt là −1 và 2. Suy ra A (−1; 0), B (2; 0).
Gọi C là giao điểm của (P) với trục Oy có tung độ bằng −2. Suy ra C (0; −2).
Theo giả thiết, (P) đi qua ba điểm A, B, C nên ta có
Vậy (P):
Câu 8:
Tìm các giá trị của tham số m để phương trình có hai nghiệm phân biệt
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
2x2 − 2x + 1 – m = 0 ⇔ 2x2 − 2x = m − 1
Số nghiệm của phương trình đã cho bằng số giao điểm của Parabol
(P): y = 2x2 − 2x và đường thẳng y = m − 1 có tính chất song song với trục hoành.
Parabol (P) có tọa độ đỉnh
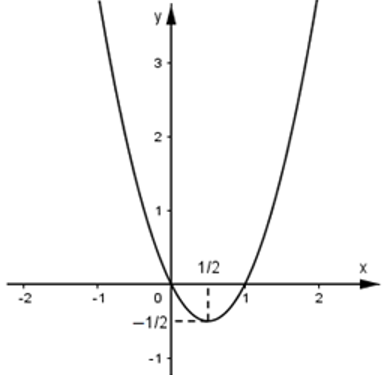
Dựa trên đồ thị ta thấy phương trình đã cho có hai nghiệm khi và chỉ khi:
Câu 9:
Biết đồ thị hàm số (P): y = x2 − (m2 + 1)x − 1 cắt trục hoành tại hai điểm phân biệt có hoành độ x1, x2. Tìm giá trị của tham số m để biểu thức T = x1 + x2 đạt giá trị nhỏ nhất.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Dễ thấy rằng phương trình hoành độ giao điểm có hai nghiệm phân biệt vì
a.c = 1.(−1) < 0 và hai giao điểm có cùng tung độ và có hoành độ đối xứng với nhau qua trục đối xứng
Từ đây suy ra T = x1 + x2 = m2 + 1 ≥ 1 ∀m
Suy ra Tmin = (x1 + x2)min = 1 và đạt được khi m = 0.
Câu 10:
Cho parabol (P): y = x2 − 4x + 3 và đường thẳng d: y = mx + 3. Tìm giá trị thực của tham số m để d cắt (P) tại hai điểm phân biệt A, B có hoành độ x1, x2 thỏa mãn
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Phương trình hoành độ giao điểm của (P) và d là x2 − 4x + 3 = mx + 3
⇔
Để d cắt (P) tại hai điểm phân biệt A, B khi và chỉ khi 4 + m ≠ 0 ⇔ m ≠ −4.
Khi đó, ta có ⇔ 0 + (4 + m)3 = 8 ⇔ 4 + m = 2 ⇔ m = −2.
Câu 11:
Tìm các giá trị của tham số m để phương trình x2 − 2(m + 1)x + 1 = 0 có hai nghiệm phân biệt trong đó có đúng một nghiệm thuộc khoảng (0; 1).
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Có: Δ′ = (m + 1)2 – 1 = m (m + 2)
Phương trình có hai nghiệm phân biệt ⇔ m (m + 2) > 0 ⇔
Khi đó dạng đồ thị hàm số y = x2 – 2 (m + 1) x + 1 chỉ có thể là:
Quan sát đồ thị ta thấy:
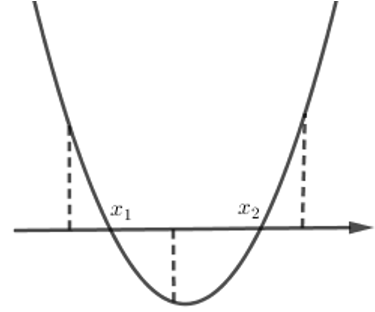
Yêu cầu bài toán tương đương f(0) . f(1) < 0 ⇔ 1.(−2m) < 0 ⇔ m > 0
Kết hợp điều kiện có hai nghiệm phân biệt ta được m > 0
Câu 12:
Tìm tất cả các giá trị thực của tham số m để phương trình có nghiệm thuộc đoạn
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
Ta có x2 − 5x + 7 + 2m = 0 ⇔ x2 − 5x + 7 = −2m. (∗)
Phương trình (∗) là phương trình hoành độ giao điểm của parabol (P): y = x2 − 5x + 7 và đường thẳng y = −2m (song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số y = x2 − 5x + 7 trên [1; 5] như sau:
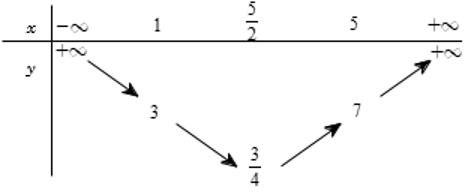
Dựa vào bảng biến ta thấy x ∈ [1; 5] thì
Do đó để phương trình (∗) có nghiệm
Câu 13:
Cho hàm số f(x) = ax2 + bx + c đồ thị như hình. Hỏi với những giá trị nào của tham số thực m thì phương trình f(|x|) – 1 = m có đúng 3 nghiệm phân biệt.
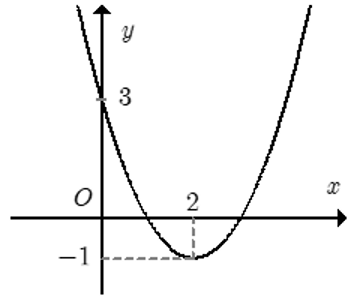
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
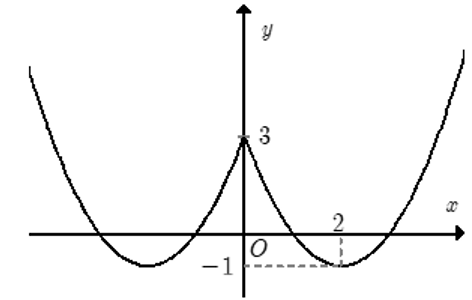
Ta có f(|x|) = f(x) nếu x ≥ 0. Hơn nữa hàm f(|x|) là hàm số chẵn. Từ đó suy ra cách vẽ đồ thị hàm số (C) từ đồ thị hàm số y = f(x) như sau:
+ Giữ nguyên đồ thị y = f(x) phía bên phải trục tung.
+ Lấy đối xứng phần đồ thị y = f(x) phía bên phải trục tung qua trục tung.
Kết hợp hai phần ta được đồ thị hàm số y = f(|x|) như hình vẽ.
Phương trình
f(|x|) – 1 = m ⇔ f(|x|) = m + 1 là phương trình hoành độ giao điểm của đồ thị hàm số y = f(|x|) và đường thẳng y = m + 1 (song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có yêu cầu bài toán ⇔ m + 1 = 3 ⇔ m = 2.
Câu 14:
Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số trên đoạn
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Hàm số có a = -1 < 0 nên bề lõm hướng xuống
Hoành độ đỉnh
Ta có
Câu 15:
Cho parabol (P): y = x2 − 4x + 3 và đường thẳng d: y = mx + 3. Tìm tất cả các giá trị thực của m để d cắt (P) tại hai điểm phân biệt A, B sao cho diện tích tam giác OAB bằng .
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Phương trình hoành độ giao điểm của (P) và d là x2 − 4x + 3 = mx + 3
Để d cắt (P) tại hai điểm phân biệt A, B khi và chỉ khi 4 + m ≠ 0 ⇔ m ≠ −4.
Với x = 0 ⇒ y = 3 ⇒ A (0; 3) ∈ Oy.
Với x = 4 + m ⇒ y = m2 + 4m + 3 ⇒ B (4 + m; m2 + 4m + 3)
Gọi H là hình chiếu của B lên OA. Suy ra BH = |xB| = |4 + m|.
Theo giả thiết bài toán, ta có
