Trắc nghiệm Tích vô hướng của hai vecto có đáp án (Vận dụng)
-
3190 lượt thi
-
15 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình chữ nhật ABCD có AB = a và AD = . Gọi K là trung điểm của cạnh AD. Tính
 Xem đáp án
Xem đáp án
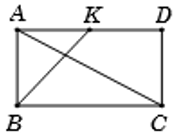
Ta có:
Đáp án cần chọn là: A
Câu 2:
Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi M là trung điểm cạnh BC. Tính
 Xem đáp án
Xem đáp án
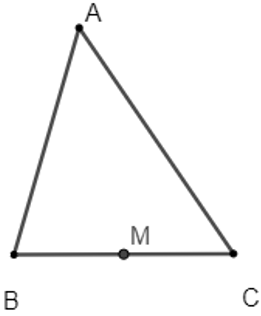
Vì M là trung điểm của BC suy ra
Khi đó
Đáp án cần chọn là: A
Câu 3:
Cho ba điểm A, B, C phân biệt. Tập hợp những điểm M mà là:
 Xem đáp án
Xem đáp án
Tập hợp điểm M là đường thẳng đi qua A và vuông góc với BC
Đáp án cần chọn là: B
Câu 4:
Tìm tập hợp các điểm M thỏa mãn với A, B, C là ba đỉnh của tam giác
 Xem đáp án
Xem đáp án
Gọi G là trọng tâm tam giác ABC
Ta có:
(*)
Biểu thức (*) chứng tỏ hay M nhìn đoạn BG dưới một góc vuông nên tập hợp các điểm M là đường tròn đường kính BG
Đáp án cần chọn là: D
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A (2; 2), B (5; −2). Tìm điểm M thuộc trục hoành sao cho ?
 Xem đáp án
Xem đáp án
Ta có nên M (m; 0) và
Vì nên suy ra nên
Đáp án cần chọn là: B
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A (−2; 4) và B (8; 4). Tìm tọa độ điểm C thuộc trục hoành sao cho tam giác ABC vuông tại C.
 Xem đáp án
Xem đáp án
Ta có nên C (c; 0) và
Vì tam giác ABC vuông tại C nên suy ra nên
Đáp án cần chọn là: B
Câu 7:
Cho A (2; 5), B (1; 3), C (5; −1). Tìm tọa độ điểm K sao cho
 Xem đáp án
Xem đáp án
Gọi K (x; y) với x, y R
Khi đó
Theo YCBT nên
Đáp án cần chọn là: B
Câu 8:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A (−3; 0), B (3; 0) và C (2; 6). Gọi H (a; b) là tọa độ trực tâm của tam giác đã cho. Tính a + 6b
 Xem đáp án
Xem đáp án
Ta có:
Từ giả thiết, ta có:
Đáp án cần chọn là: C
Câu 10:
Trong mặt phẳng tọa độ Oxy, cho ba vec tơ và với . Biết rằng vec tơ vuông góc với vec tơ . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
Để
Đáp án cần chọn là: C
Câu 11:
Trong mặt phẳng tọa độ Oxy, cho ba vec tơ và với . Tìm m để vuông góc với trục hoành
 Xem đáp án
Xem đáp án
Ta có:
Trục hoành có vectơ đơn vị là:
Vec tơ vuông góc với trục hoành
Đáp án cần chọn là: B
Câu 12:
Trong mặt phẳng tọa độ Oxy, cho hai vec tơ . Tìm m để tạo với vec tơ một góc 450
 Xem đáp án
Xem đáp án
Ta có:
Yêu cầu bài toán
Đáp án cần chọn là: C
Câu 13:
Trong mặt phẳng tọa độ Oxy, cho bốn điểm A (7; −3), B (8; 4), C(1;5) và D (0; −2). Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
Lại có nên
Từ đó suy ra ABCD là hình vuông
Đáp án cần chọn là: C
Câu 14:
Trong mặt phẳng tọa độ Oxy, cho bốn điểm . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Ta có:
Suy ra DC//AB và DC = 3AB (1)
Mặt khác (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình thang cân
Đáp án cần chọn là: C
Câu 15:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có . Tìm tọa độ chân đường cao A’ vẽ từ đỉnh A của tam giác đã cho
 Xem đáp án
Xem đáp án
Gọi A’ (x, y). Ta có:
Từ giả thiết, ta có A’ là chân đường cao vẽ từ đỉnh A của tam giác ABC nên và B, A’, C thẳng hàng
Đáp án cần chọn là: D
