Trắc nghiệm Toán 10 Bài 4. Tích vô hướng của hai vectơ có đáp án
-
418 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hình chữ nhật ABCD có AB = , AD = 1. Tính góc giữa hai vectơ và .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
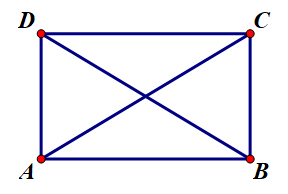
Tam giác ACD vuông tại D: .
Tam giác ABC vuông tại B: .
Ta có .
.
Vì ABCD là hình chữ nhật nên ta có CD = AB = và AC = BD.
Tam giác ACD vuông tại D: (Định lý Pytago)
.
Do đó BD = AC = .
Lại có:
.
.
Vậy ta chọn đáp án C.
Câu 2:
Cho tam giác đều ABC có đường cao AH. Tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
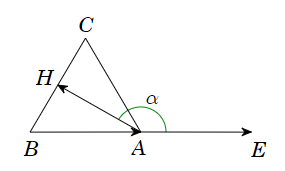
Vẽ .
Khi đó ta có .
Tam giác ABC đều có AH là đường cao.
Suy ra AH cũng là đường phân giác của tam giác ABC.
Tam giác ABC đều, suy ra .
Do đó .
Ta có: (hai góc kề bù)
.
Vậy ta chọn đáp án D.
Câu 3:
Cho và là hai vectơ cùng hướng và đều khác . Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có .
Vì và là hai vectơ cùng hướng và đều khác nên , suy ra .
Ta suy ra
Vậy ta chọn đáp án A.
Câu 4:
Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có
⇔ OB = OA.
Do đó tam giác OAB cân tại O.
Vậy ta chọn đáp án B.
Câu 5:
Cho hai vectơ và thỏa mãn , và . Xác định góc α giữa hai vectơ và .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có
.
Vậy ta chọn đáp án D.
Câu 6:
Cho M, N, P, Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Đáp án A đúng theo tính chất phân phối của tích vô hướng.
Đáp án B sai. Sửa lại: .
Đáp án C đúng theo tính chất giao hoán của tích vô hướng.
Đáp án D đúng, ta sử dụng bình phương vô hướng và hằng đẳng thức.
Câu 7:
Cho AB = 2cm, BC = 3cm, CA = 5cm. Tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có 2 + 3 = 5 (cm). Ta suy ra AB + BC = AC.
Do đó ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C.
(A, B, C không thể là ba đỉnh của tam giác vì không thỏa mãn bất đẳng thức tam giác).
Suy ra . Do đó .
Khi đó .
Vậy ta chọn đáp án B.
Câu 8:
Cho hình vuông ABCD cạnh a. Tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Tam giác ABC vuông tại B: AC2 = AB2 + BC2 (Định lý Pytago)
⇔ AC2 = a2 + a2 = 2a2
.
Vì ABCD là hình vuông có AC là đường chéo nên .
Ta có
.
Vậy ta chọn đáp án C.
Câu 9:
Cho hình vuông ABCD tâm O. Tính tổng .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
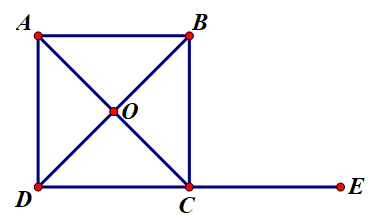
Ta có cùng hướng nên .
Ta có ngược hướng nên .
Vẽ . Khi đó ta có .
Vì ABCD là hình vuông có OC là đường chéo nên .
Ta có BC ⊥ CD (ABCD là hình vuông)
Suy ra BC ⊥ CE, do đó .
Ta có .
Vậy .
Vậy ta chọn đáp án C.
Câu 10:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có .
Tam giác ABC đều nên .
Do đó .
Suy ra .
Vậy ta chọn đáp án D.
Câu 11:
Cho tam giác ABC có BC = a, CA = b, AB = c. Tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có
.
Vậy ta chọn đáp án A.
Câu 12:
Cho hình chữ nhật ABCD có AB = 8, AD = 5. Tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Vì giả thiết không cho góc nên ta sẽ phân tích các vectơ theo các vectơ vuông góc với nhau.
Vì ABCD là hình chữ nhật nên AB ⊥ BC.
Suy ra .
Do đó .
Theo quy tắc hình bình hành ta có: .
Ta có
.
Vậy ta chọn đáp án D.
Câu 13:
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có .
Vậy tập hợp các điểm M là đường thẳng đi qua A và vuông góc với BC.
Vậy ta chọn đáp án B.
Câu 14:
Cho tam giác ABC vuông tại A và AB = AC = a. Tính .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
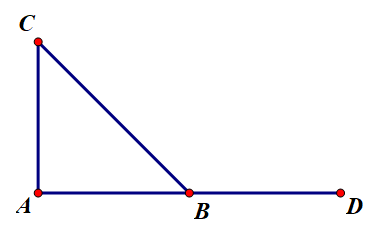
Vẽ .
Ta có .
Tam giác ABC vuông cân tại A. Ta suy ra .
Ta có (hai góc kề bù)
Khi đó ta được .
Tam giác ABC vuông cân tại A: BC2 = AB2 + AC2 (Định lý Pytago)
⇔ BC2 = 2a2
.
Do đó .
Vậy ta chọn đáp án A.
Câu 15:
Cho tam giác ABC. Tập hợp các điểm M thỏa mãn là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Gọi I là trung điểm BC. Ta suy ra .
Ta có (*)
Biểu thức (*) chứng tỏ MA ⊥ MI hay M nhìn đoạn AI dưới một góc vuông.
Do đó tập hợp các điểm M là một đường tròn đường kính AI.
Vậy ta chọn đáp án D.
