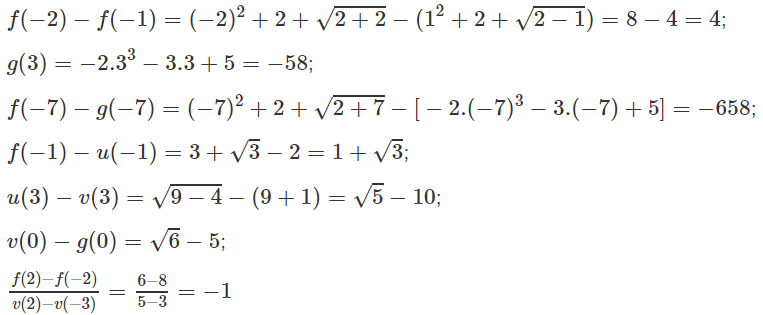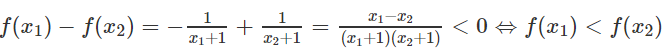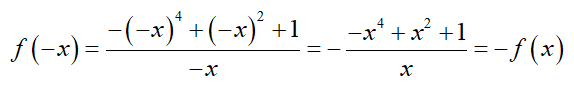9 câu hỏi trắc nghiệm thuộc Bài 1: Hàm số - SBT Đại số 10

Giải SBT Toán 10 Đại số - Chương 2: Hàm số bậc nhất và bậc hai

Bài 1: Hàm số - SBT Đại số 10

802 lượt thi
9 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

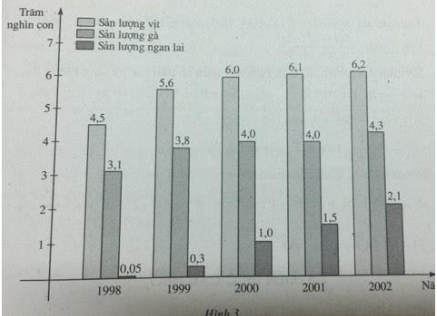
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y = f(x), y = g(x) và y = h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian x. Qua biểu đồ, hãy:

a) Tìm tập xác định của mỗi hàm số đã nêu.

b) Tìm các giá trị f(2002), g(1999), h(2000) và nêu ý nghĩa của chúng;

c) Tìm hiệu h(2002) – h(1999) và nêu ý nghĩa của nó.

Xem đáp án

a) Tập xác định của cả ba hàm số y = f(x), y = g(x) và y = h(x) là:

D = {1998, 1999, 2000, 2001, 2002}

b) f(2002) = 620000 (con)

g(1999) = 380000 (con)

h(2000) = 100000 (con)

Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.

c) h(2002) - h(1999) = 210000 - 30000 = 180000 (con)

Sản lượng ngan lai của trang trại năm 2002 tăng 180 000 con so với năm 1999.

Câu 2:

Tìm tập xác định của các hàm số

a) y = -x⁵ + 7x - 3

b) $y = \frac{3 x + 2}{x - 4}$

c) $y = \sqrt{4 x + 1} - \sqrt{- 2 x + 1}$

d) $y = \frac{2 x + 1}{(2 x + 1) (x - 3)}$

Xem đáp án

a) D = R;

b) D = R\ {4};

c) Hàm số xác định với các giá trị của x thỏa mãn

4x + 1 ≥ 0 và -2x + 1 ≥ 0 hay x ≥ -x / 4 ≤ -1/2

Vậy tập xác định của hàm số đã cho là D = [-1/4; 1/2]

d) D = R \ {-1/2; 3}

Câu 3:

Cho hàm số

$y = f (x) = \{\begin{cases} \frac{2 x - 3}{x - 1}; x \leq 0 \\ - x^{2} + 2 x; x > 0 \end{cases}$

Tính giá trị của hàm số đó tại x = 5; x = -2; x = 0; x = 2.

Xem đáp án

f(5) = -5² + 2.5 = -25 + 10 = -15 vì (5 > 0)

f(-2) = 7/3

f(0) = 3

f(2) = 0

Câu 4:

Cho các hàm số

$f (x) = x^{2} + 2 + \sqrt{2 - x}; g (x) = - 2 x^{3} - 3 x + 5 u (x) = \{\begin{cases} \sqrt{3 - x}, x < 2 \\ \sqrt{x^{2} - 4}, x \geq 2 \end{cases} v (x) = \{\begin{cases} \sqrt{6 - x}, x \leq 0 \\ x^{2} + 1, x > 0 \end{cases}$

Tính các giá trị

$f (- 2) - f (1); g (3); f (- 7) - g (- 7); f (- 1) - u (- 1); u (3) - v (3); v (0) - g (0); \frac{f (2) - f (- 2)}{v (2) - v (- 3)}$

Xem đáp án

Câu 5:

Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng

a) y = -2x + 3 trên R

b) y = x² + 10x + 9 trên (-5; +∞)

c) $y = - \frac{1}{x + 1}$ trên (-3; 2) và (2; 3)

Xem đáp án

a) ∀ x₁, x₂ ∈ R ta có:

f(x₁) - f(x₂) = -2x₁ + 3 - (-2x₂ + 3) = -2(x₁ - x₂)

Ta thấy x₁ > x₂ thì 2(x₁ - x₂) < 0 tức là:

f(x₁) - f(x₂) < 0 ⇔ f(x₁) &ly; f(x₂)

Vậy hàm số đã cho nghịch biến trên R.

b) ∀ x₁, x₂ ∈ R ta có:

f(x₁) - f(x₂) = x₁² + 10x₁ + 9 - x₂² - 10x₂ - 9

= (x₁ - x₂)(x₁ + x₂) + 10(x₁ - x₂)

= (x₁ - x₂)(x₁ + x₂ + 10) (∗)

∀ x₁, x₂ ∈ (-5; +∞) và x₁ < x₂ ta có x₁ - x₂ < 0 và x₁ + x₂ + 10 > 0 vì

x₁ > -5; x₁ > -5; ⇒ x₁ + x₂ > -10

Vậy từ (∗) suy ra f(x₁) - f(x₂) < 0 ⇔ f(x₁) < f(x₂)

Hàm số đồng biến trên khoảng (-5; +∞)

c) ∀ x₁, x₂ ∈ (-3; -2) và x₁ < x₂, ta có:

x₁ - x₂ < 0;

x₁ + 1 < -2 + 1 < 0;

x₂ + 1 < -2 + 1 < 0;

⇒ (x₁ + 1)(x₂ + 1) > 0.

Vậy

Do đó hàm số đồng biến trên khoảng (-3; -2)

∀ x₁, x₂ ∈ (-3; -2) và x₁ < x₂ tương tự ta cũng có f(x₁) < f(x₂)

Vậy hàm số đồng biến trên khoảng (2;3).

Câu 6:

Xét tính chẵn, lẻ của các hàm số

a) y = -2;

b) y = 3x² - 1;

c) y = -x⁴ + 3x - 2;

d) $y = \frac{- x^{4} + x^{2} + 1}{x}$

Xem đáp án

a) Tập xác định D = R và ∀ x ∈ D có -x ∈ D và f(-x) = -2 = f(x)

Hàm số là hàm số chẵn

b) Tập xác định D = R; ∀ x ∈ D có -x ∈ D và f(-x) = 3.(-x)² - 1 = 3x² - 1 = f(x)

Vậy hàm số đã cho là hàm số chẵn.

c) Tập xác định D = R, ∀ x ∈ D có -x ∈ D và f(-x) = -(-x)⁴ + 3(-x) - 2 = -x⁴ - 3x - 2

Ta thấy rằng f(-x) ≠ f(x) và f(-x) ≠ -f(x).

Vậy hàm số đã cho không là hàm số chẵn cũng không là hàm số lẻ.

d) Tập xác định D = R\{0} nên nếu x ≠ 0 và x ∈ D thì -x ∈ D. Ngoài ra

Câu 7:

Tập xác định của hàm số sau là

$y = \frac{3 x + 10}{x^{2} + 14 x + 45}$

A. R

B. R \ {-5; 9}

C. R \ {-5, -9}

D. R \ {5; 9}

Xem đáp án

Đáp án: C (vì x² + 14x + 45 ≠ 0 ⇔ x ≠ -5 và x ≠ -9).

Câu 8:

Hàm số sau có tập xác định D bằng:

$y = \sqrt{x + 7} + \frac{2}{x^{2} + 6 x - 16}$

A. [7; +∞)

B. (-7; +∞) \ {-8; 2}

C. [-7; 7] \ {2}

D. [-7; +∞) \ {2}

Xem đáp án

Đáp án: D (vì x ≥ -7 và x² + 6x – 16 ≠ 0 ⇔ x ≠ -8 và x ≠ 2)

Câu 9:

Cho các hàm số:

$f (x) = \{\begin{cases} x^{2} - 1 với x \leq 3 \\ \sqrt{x + 2} với x > 3 \end{cases} f (x) = \{\begin{cases} 2 x + 3 với x > 1 \\ x^{2} + 2 với x \leq 1 \end{cases}$

Khi đó giá trị: f(0) + 2f(7) - g(1) bằng:

A. 2

B. 0

C. √2 + 3

D. -2

Xem đáp án

Đáp án: A (vì f(0) = -1; f(7) = 3 và g(1) = 3).

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Đại số - Chương 2: Hàm số bậc nhất và bậc hai

Bài 1: Hàm số - SBT Đại số 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương