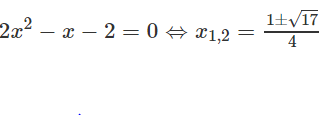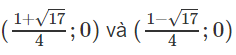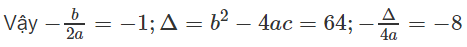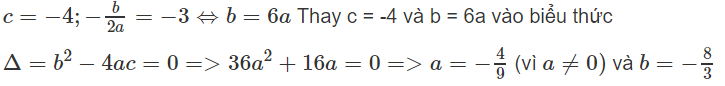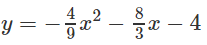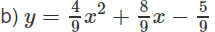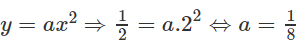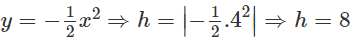Bài 3: Hàm số bậc hai - SBT Đại số 10
-
799 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.
a) y = 2x2 - x - 2
b) y = -2x2 - x + 2
 Xem đáp án
Xem đáp án
a) Ở đây a = 2; b = -2; c = -2. Ta có Δ = (-1)2 - 4.2.(-2) = 17
Trục đối xứng là đường thẳng x = 1/4; đỉnh I(1/4; -17/8) giao với trục tung tại điểm (0; -2).
Để tìm giao điểm với trục hoành ta giải phương trình
Vậy các giao điểm với trục hoành là
b) Trục đối xứng x = -1/4; đỉnh I(-1/4; -17/8) giao với trục tung tại điểm (0;2); giao với trục hoành tại các điểm
Câu 2:
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
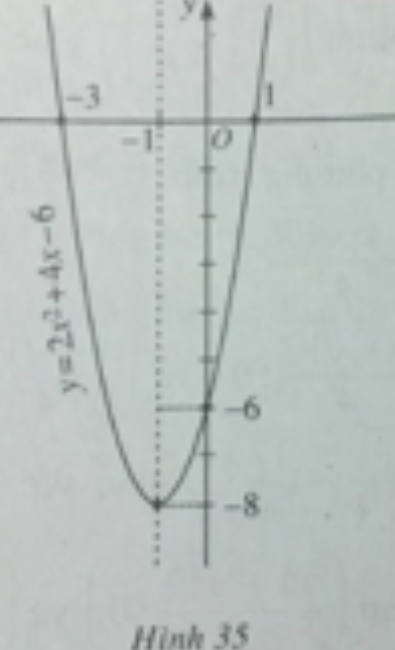
a) y = 2x2 + 4x - 6;
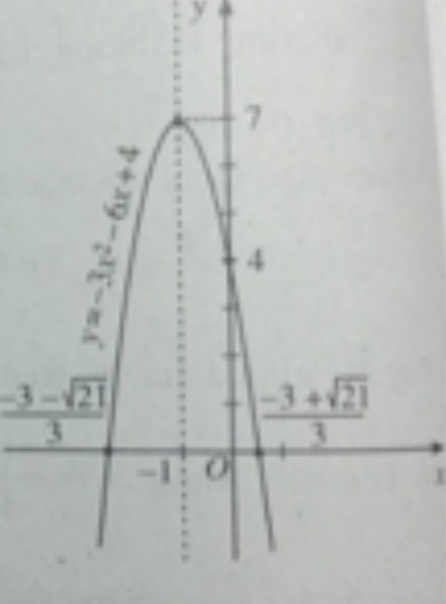
b) y = -3x2 - 6x + 4;
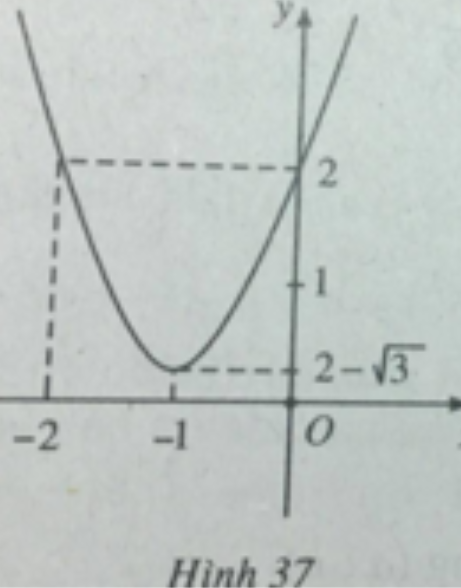
c) y = √3x2 + 2√3x + 2;
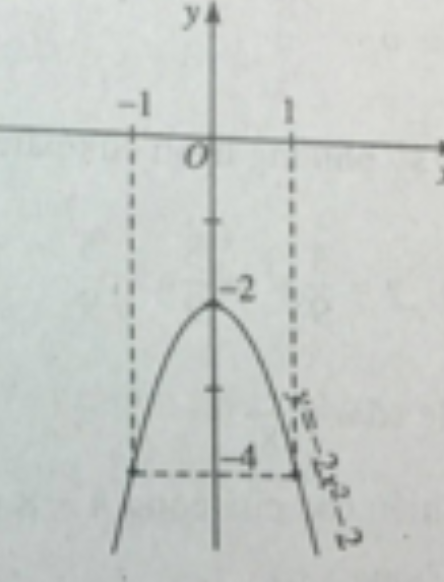
d) y = -2(x2 + 1)
 Xem đáp án
Xem đáp án
a) Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;
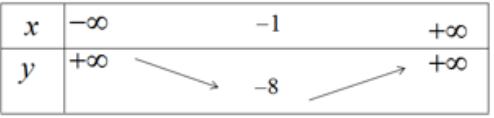
Vì a > 0, ta có bảng biến thiên
Hàm số nghịch biến trên khoảng (-∞; -1) đồng biến trên khoảng (-1; +∞)
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).
Đồ thị của hàm số y = 2x2 + 4x - 6 được vẽ trên hình 35.
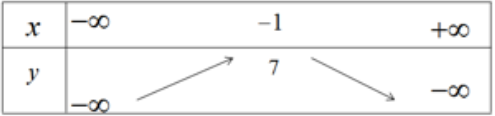
b) Bảng biến thiên
Hàm số đồng biến trên khoảng (-∞; -1) nghịch biến trên khoảng (-1; +∞)
Đỉnh parabol I(-1;7). Đồ thị của hàm số y = -3x2 - 6x + 4 được vẽ trên hình 36.
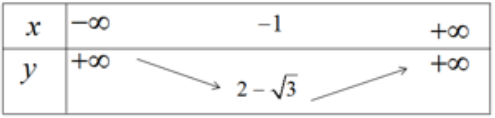
c) Bảng biến thiên
Hàm số nghịch biến trên khoảng (-∞; -1) đồng biến trên khoảng (-1; +∞)
Đỉnh parabol (-1; 2 - √3)
Đồ thị hàm số được vẽ trên hình 37.
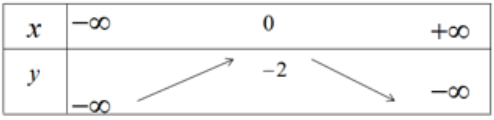
d) Bảng biến thiên
Hàm số đồng biến trên khoảng (-∞; 0) nghịch biến trên khoảng (0; +∞), hàm số là chẵn.
Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4).
Đồ thị hàm số y = -2(x2 + 1) được vẽ trên hình 38.
Câu 3:
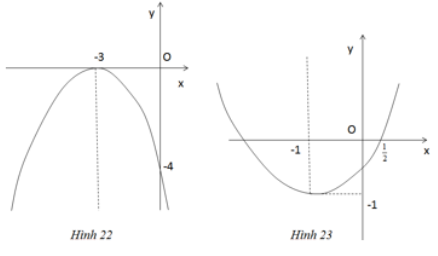
Viết phương trình của parabol y = ax2 + bx + c ứng với mỗi đồ thị dưới đây
 Xem đáp án
Xem đáp án
a) Dựa trên đồ thị (h.22) tâ thấy parabol có đỉnh I(-3 ;0) và đi qua điểm (0 ;-4). Như vậy
Vậy phương trình của parabol là
Câu 4:
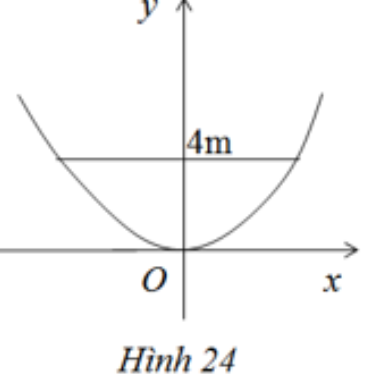
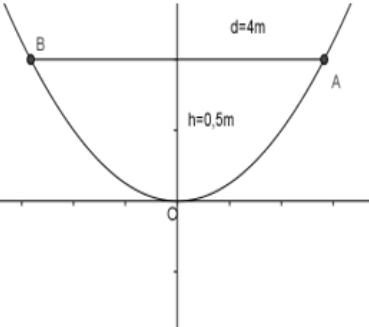
Một chiếc ăng – ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4 m. Ở mặt cắt qua trục ta được một parabol dạng y = ax2(h.24). Hãy xác định hệ số a.
 Xem đáp án
Xem đáp án
Ta có thiết diện mặt cắt qua trục của chiếc ăng-ten là:
Vậy ta có: A(2; 1/2) mà A ∈ prapol:
Câu 5:
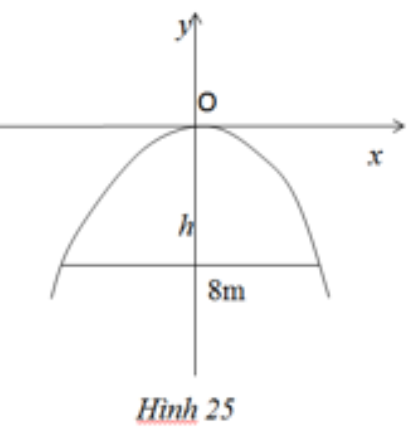
Một chiếc cổng hình parabol dạng y = -x2 / 2 có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).
 Xem đáp án
Xem đáp án
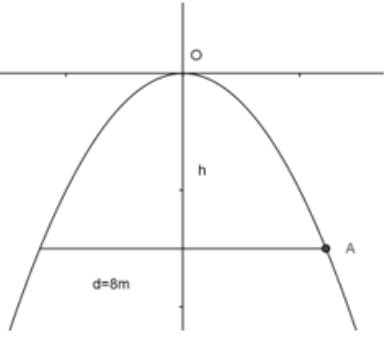
Ta có: A(4; -h) mà A ∈ parabol
Câu 6:
Tọa độ định của parabol y = (-x2 / 2) + 6x + 1 là
 Xem đáp án
Xem đáp án
Đáp án: A (hoành độ đỉnh là x = (-b)/2a = 6; tung độ đỉnh là y = (-Δ)/4a = 19).
Câu 7:
Trục đối xứng của parabol y = (x2 / 5) + 2x + 7 là
 Xem đáp án
Xem đáp án
Đáp án: C (trục đối xứng là đường thẳng x = (-b)/2a).
Câu 8:
Hàm số bậc hai y = ax2 + bx - 6 có đồ thị đi qua hai điểm A(1; 1) và B(2; 2) là
 Xem đáp án
Xem đáp án
Đáp án: B (có thể kiểm tra trực tiếp).
Câu 9:
Hàm số bậc hai y = ax2 - 2x + c có đồ thị với đỉnh I(2; -1) là
 Xem đáp án
Xem đáp án
Đáp án: A (kiểm tra hoành độ đỉnh x = (-b)/2a; sai đó kiểm tra tung độ đỉnh).