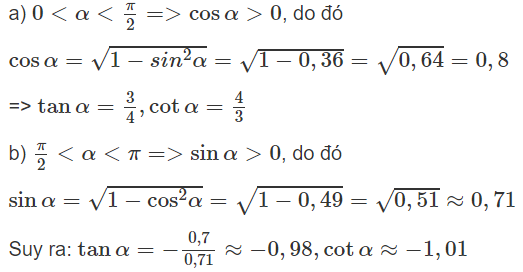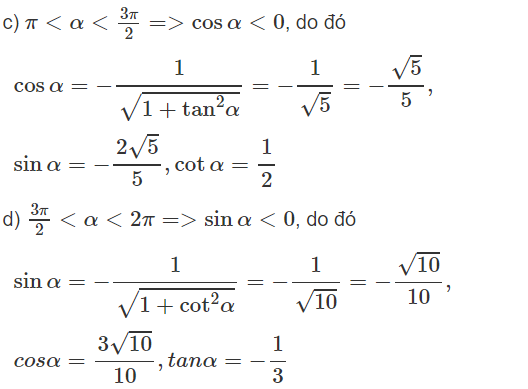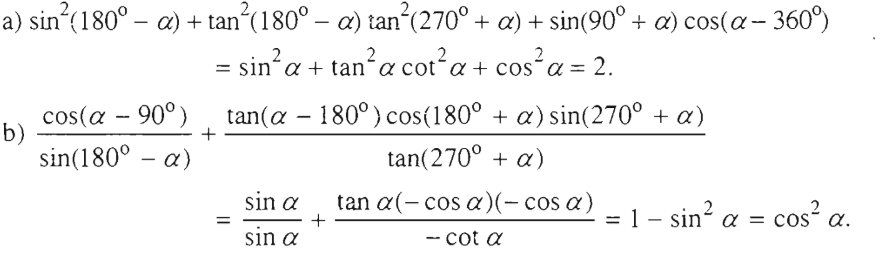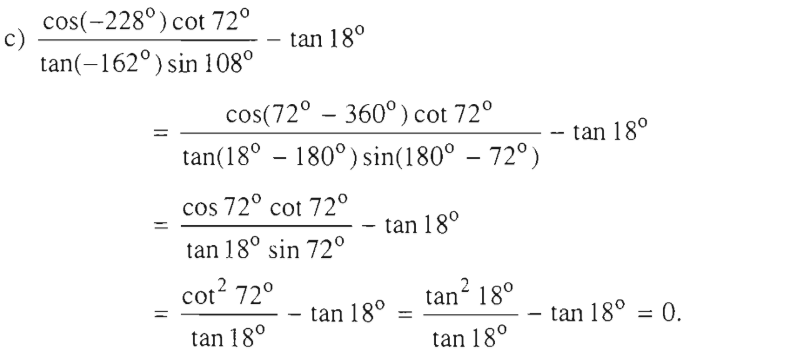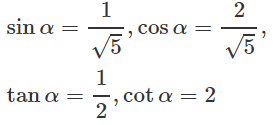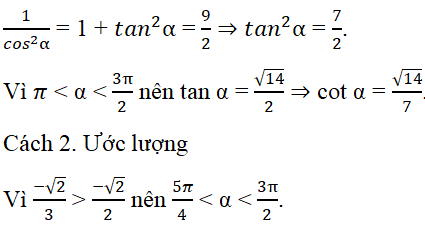18 câu hỏi trắc nghiệm thuộc Ôn tập chương 6 - SBT Đại số 10

Câu 1:

Trong các đẳng thức sau, đẳng thức nào đúng, đẳng thức nào sai?

a) sin(x + π/2) = cosx;

b) cos(x + π/2) = sinx;

c) sin(x - π) = sinx;

d) cos(x - π) = cosx

Xem đáp án

a) Đúng;

b) Sai;

c) Sai;

d) Sai.

Câu 2:

Tồn tại hay không góc α sao cho

a) sinα = -1; b) cosα = 0;

c) sinα = -0,9; d) cosα = -1,2;

e) sinα = 1,3; e) cosα = -2.

Xem đáp án

a) Có;

b) Có;

c) Có;

d) Không, vì -1,2 <-1.

e) Không, vì 1,3 > 1;

g) Không, vì -2 < -1.

Câu 3:

Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với

a) α = 135^ο b) α = 210^ο

c) α = 334^ο d) α = 1280^ο

e) α = -235^ο e) α = -1876^ο

Xem đáp án

a) sin 135^ο > 0, cos 135^ο < 0

b) sin 210^ο < 0, cos 210^ο < 0

c) sin 334^ο < 0, cos 334^ο > 0

d) sin 1280^ο = sin(3. 360^ο + 120^ο) = sin 200^ο < 0

cos 1280^ο = cos 200^ο < 0

e) sin(-235^ο) = sin(-180^ο - 55^ο) = -sin(-55^ο) = sin 55^ο > 0, cos(-235^ο) < 0

g) sin(-1876^ο) = sin(-1800^ο - 76^ο) = sin(-76^ο) = -sin 76^ο < 0

cos(-1876^ο) = cos(-76)^ο = cos 76^ο > 0

Câu 4:

Hãy viết theo thứ tự tăng dần các giá trị sau (không dùng bảng số và máy tính)

a) sin 40^ο, sin 90^ο, sin 220^ο, sin 10^ο;

b) cos 15^ο, cos 0^ο, cos 90^ο, cos 138^ο.

Xem đáp án

a) sin 220^ο < sin 10^ο < sin 40^ο < sin 90^ο

b) cos 138^ο < cos 90^ο < cos 15^ο < cos 0^ο

Câu 5:

Hãy xác định dấu của các tích (không dùng bảng số và máy tính)

a) sin 110^ο cos 130^ο cos 30^ο cot 320^ο

b) sin(-50^ο) tan 170^ο cos(-91^ο) sin 530^ο.

Xem đáp án

a) Ta có: sin 110^ο > 0; cos 130^ο < 0; tan 30^ο > 0; cot 320^ο < 0, do đó tích của chúng dương.

b) sin(-50^ο) < 0; tan 170^ο < 0; cos(-90^ο) < 0; sin 530^ο > 0, do đó tích của chúng âm

Câu 6:

Cho tam giác ABC. Hỏi tổng sinA + sinB + sinC âm hay dương

Xem đáp án

Vì các góc A, B, C là góc trong tam giác ABC nên sinA > 0, sinB > 0, sinC > 0.

Do đó sinA + sinB + sinC > 0.

Câu 7:

Tính các giá trị lượng giác của cung α biết

a) $sinα = 0, 6 khi 0 < α < \frac{π}{2}$

b) $cosα = - 0, 7 khi \frac{π}{2} < α < π$

c) $tanα = 2 khi π < α < \frac{3 π}{2}$

d) $tanα = - 3 khi \frac{3 π}{2} < α < 2 π$

Xem đáp án

Câu 8:

Chứng minh rằng

a) sin(270^ο - α) = -cosα;

b) cos(270^ο - α) = -sinα;

c) sin(270^ο + α) = -cosα;

d) cos(270^ο + α) = sinα.

Xem đáp án

a) sin(270^ο - α) = sin(360^ο - (90^ο + α)) = -sin(90^ο + α) = -cosα

b) cos(270^ο - α) = cos(360^ο - (90^ο + α)) = cos(90^ο + α) = -sinα

c) sin(270^ο + α) = sin(360^ο - (90^ο - α)) = -sin(90^ο - α) = -cosα

d) cos(270^ο + α) = cos(360^ο - (90^ο - α)) = cos(90^ο - α) = sinα

Câu 9:

Rút gọn các biểu thức (không dùng bảng số và máy tính)

$a) \sin^{2} (180^{o} - α) + \tan^{2} (180^{o} - α) \tan^{2} (270^{o} + α) + \sin (90^{o} + α) \cos (α - 360^{o}) b) \frac{\cos (α - 90^{o})}{\sin (180^{o} - α)} + \frac{\tan (α - 180^{o}) \cos (180^{o} + α) \sin (270^{o} + α)}{\tan (270^{o} + α)} c) \frac{\cos (- 288^{o}) \cot 72^{o}}{\tan (- 162^{o}) \sin 108^{o}} - \tan 18^{o} d) \frac{\sin 20^{o} \sin 30^{o} \sin 40^{o} \sin 50^{o} \sin 60^{o} \sin 70^{o}}{\cos 10^{o} \cos 50^{o}}$

Xem đáp án

Câu 10:

Cho 0^ο < α < 90^ο

a) Có giá trị nào của α sao cho tanα < sinα hay không?

b) Chứng minh rằng sinα + cosα > 1.

Xem đáp án

Với 0^ο < α < 90^ο thì 0 < cosα < 1 hay 1/cosα > 1

Nhân hai về với sinα > 0 ta được tanα > sinα

Vậy không có giá trị nào của α (0^ο < α < 90^ο) để tanα < sinα

b) Ta có sinα + cosα > 0 và sinαcosα > 0. Do đó

(sinα + cosα)² = sin²α + cos²α + 2sinαcosα = 1 + 2sinαcosα > 1

Từ đó suy ra: sinα + cosα > 1

Câu 11:

Tính các giá trị lượng giác của góc α, biết

a) cosα = 2sinα khi 0 < α < π/2

b) cotα = 4tanα khi π/2 < α < π.

Xem đáp án

a) Với 0 < α < π/2 thì cosα >0, sinα >0. Ta có

1 - sin²α = cos²α

Mặt khác cos²α = (2sinα)² = 4sin²α nên 5sin²α = 1 hay

b) Với π/2 < α < π thì sinα > 0, cosα < 0, tanα < 0

Câu 12:

Chứng minh rằng các biểu thức sau là những số không phụ thuộc α

a) A = 2(sin⁶α + cos⁶α) - 3(sin⁴α + cos⁴α)

b) B = 4(sin⁴α + sin⁴α) - cos4α

c) C = 8(cos⁸α - sin⁸α) - cos6α - 7cos2α

Xem đáp án

a) A = 2(sin²α + cos²α)(sin⁴α + cos⁴α - sin²αcos²α) - 3(sin⁴α + cos⁴α)

= -sin⁴α - cos⁴α - 2sin²αcos²α

= -(sin²α + cos²α)² = -1

b) A = 4[(sin²α + cos²α)² - 2sin²αcos²α] - cos4α

= 4(1 - sin²2α/2) - 1 + 2sin²2α = 3

Câu 13:

Cho tam giác ABC không tù, thỏa mãn điều kiện

cos2A + 2√2cosB + 2√2cosC = 3

Tính các góc của tam giác ABC

Xem đáp án

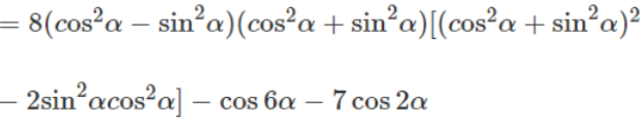
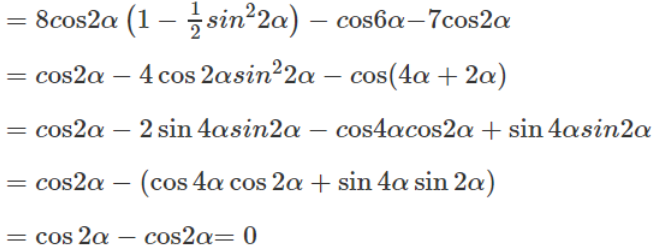
Câu 14:

Số đo của góc 5π/8 đổi ra độ là

A. $79^{o}$

B. 1 $112, 5^{o}$

C. $125, 5^{o}$

D. $87, 5^{o}$

Xem đáp án

Cách 1. Tính trực tiếp.

5π/8 = 5/8.180^o = 112,5^o.

Cách 2. Ước lượng.

90^o = π/2 < 5π/8 < 2π/3 = 120^o.

Do các phương án A, C, D bị loại. Đáp án là B.

Đáp án: B

Câu 15:

Một đường tròn có đường kính 24cm. Độ dài của cung trên đường tròn đó có số đo 30^ο xấp xỉ là

A. 6,3cm

B. 6,4cm

C. 7,5cm

D. 5,8cm

Xem đáp án

Đổi 30^o ra radian rồi dùng công thức l = Rα.

Đáp án: A

Câu 16:

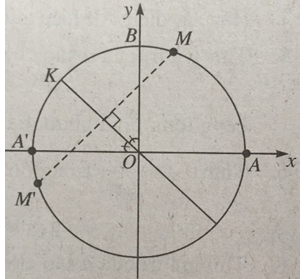
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = 80^ο trong đó A(1; 0). Gọi M' là điểm đối xứng với M qua đường phân giác của góc phần tư thứ II. Số đo của cung lượng giác AM' là:

A. $170^{o}$

B. $- 200^{o}$

C. $190^{o}$

D. $280^{o}$

Xem đáp án

Sđ MK = sđ KM’ = 55^o

⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190^o.

Đáp án: C

Câu 17:

Giá trị sin 570^ο là

A. √3/2

B. -1/2

C. 1/3

D. √2/2

Xem đáp án

sin570^o = sin(540^o + 30^o) = -sin30^o = (-1)/2.

Đáp án: B

Câu 18:

Cho cosα = -√2/3 với π < α < 3π/2. Giá trị cotα là:

A. $\frac{- \sqrt{14}}{7}$

B. $\frac{\sqrt{14}}{3}$

C. $\frac{14}{3}$

D. $\frac{\sqrt{14}}{7}$

Xem đáp án

Cách 1. Tính trực tiếp.

Suy ra 0 < cot α < 1. Vậy các phương án A, B, C bị loại.

Đáp án: D

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Đại số - Chương 6: Cung và góc lượng giác. Công thức lượng giác

Ôn tập chương 6 - SBT Đại số 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương