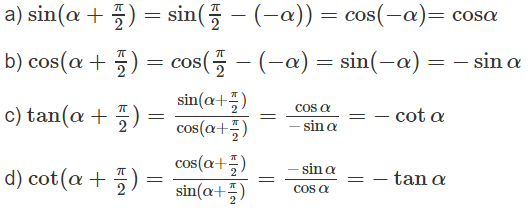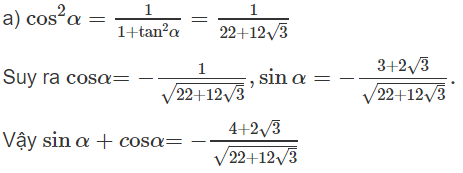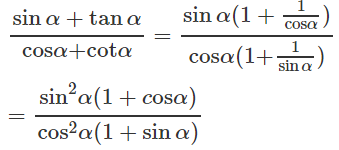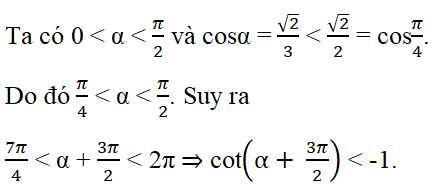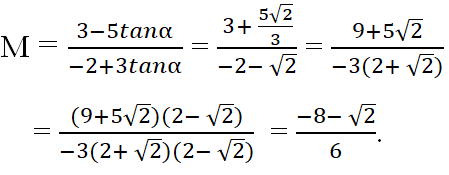Giải SBT Toán 10 Đại số - Chương 6: Cung và góc lượng giác. Công thức lượng giác
Bài 2: Giá trị lượng giác của một cung - SBT Đại số 10
-
2088 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho π < α 3π/2. Xác định dấu của các giá trị lượng giác sau
a) cos(α - π/2) b) sin(π/2 + α)
c) tan(3π/2 - α) d) cot(α + π)
Xem đáp án
a) Vì π < α 3π/2 thì π/2 < α - π/2 < π, do đó cos(α - π/2) < 0
b) 3π/2 < π/2 + α < 2π nên sin(π/2 + α) < 0
c) 0 < 3π/2 - α < π/2 nên tan(3π/2 - α) > 0
d) π < α + π < 5π/2 nên cot(α + π) > 0
Câu 4:
Cho tanα - 3cotα = 6 và π < α < 3π/2. Tính
a) sinα + cosα;
b)
Xem đáp án
Vì π < α 3π/2
Nên cosα < 0, sinα < 0 và tanα > 0
Ta có tanα - 3cotα = 6 ⇔ tanα - 3/α - 6 = 0
tan2α - 6α - 3 = 0
Vì tanα < 0 nên tanα = 3 + 2√3
b)
Câu 5:
Cho tanα + cotα = m, hãy tính theo m
a) tan2α + cot2α
b) tan3α + cot3α
Xem đáp án
a) tan2α + cot2α = (tanα + cotα)2 - 2tanαcotα = m2 - 2
b) tan3α + cot3α = (tanα + cotα)(tan2α - tanαcotα + cot2α) = m(m2 - 3)
Câu 7:
Chứng minh rằng với mọi α làm cho biểu thức có nghĩa, biểu thức đó không thể là một số âm.
Xem đáp án
Ta có:
Vì 1 + cosα ≥ 0 và 1 + sinα ≥ 0 cho nên biểu thức đã cho không thể có giá trị là một số âm.
Câu 9:
Cho sinα = -2√5/5 với 3π/2 < α < 2π. Giá trị cotα là
Xem đáp án
cot2 α = 1/( sin2 α) – 1 = 25/20 – 1 = 1/4 ⇒ cotα = ±1/2.
Vì 3π/2 < α < 2π nên cotα < 0. Vậy cotα = (-1)/2.
Đáp án: C
Câu 10:
Cho cotα = -2/3 với π < α < π. Giá trị cosα là
Xem đáp án
Cách 1.
1/( sin2 α) = 1 + cot2 α = 1 + 4/9 = 13/9 ⇒ sin2 α = 9/13.
Suy ra sinα = ±3/√13.
Vì π/2 < α < π nên sinα > 0. Vậy sinα = 3/√13.
Từ đó cosα = sinα.cotα = (-2)/√13.
Đáp án là A.
Cách 2.
cotα = (-2)/3 ⇒ tanα = (-3)/2;
1/( cos2 α) = 1 + tan2 α = 1 + 9/4 = 13/4 ⇒ cos2 α = 4/13.
Suy ra cosα = ±2/√13. Vì π/2 < α < π nên cosα < 0.
Vậy cosα = (-2)/√13 và đáp án là A.
Đáp án: A
Câu 11:
Cho tanα = -√2/3. Giá trị của biểu thức là
Xem đáp án
Cách 1. Suy luận
Vì tanα < 0 nên cosα và sinα trái dấu.
Nếu cosα > 0, sinα < 0 thì tử số của M dương, còn mẫu số âm, nên M < 0. Còn nếu cosα < 0, sinα > 0 thì tử số của M âm, mẫu số của M dương nên ta cũng có M < 0.
Do đó các phương án A, C, D bị loại và đáp án là B.
Cách 2. Tính trực tiếp.
Chi cả tử và mẫu của M sao cho cosα, ta được
Đáp án: B
Câu 12:
Cho cosα = √2/3 (0 <α < π/2 ). Giá trị của cot(α + 3π/2) là
Xem đáp án
Vậy các phương án B, C, D bị loại và đáp án là A.
Đáp án: A
Câu 13:
Cho tanα + cotα = -2. Giá trị của biểu thức N = tan3α + cot3α là
Xem đáp án
Cách 1.
Ta có tanα + cotα = tanα + 1/tanα.
Do đó tanα + cotα ≤ -2 hoặc tanα + cotα ≥ 2.
Dấu “=” xảy ra khi tanα = cotα = -1 hoặc tanα = cotα = 1.
Với giả thiết tanα + cotα = -2 thì tanα = cotα = -1.
Do đó tan3 α + cot3 α = -2
Đáp án là C.
Cách 2.
Áp dụng công thức
tan3 α + cot3 α = (tanα + cotα)( tan2 α – tanα.cotα + cot2 α)
= -2( tan2 α + cot2 α – 1)
Mà tan2 α + cot2 α = (tanα + cotα)2 - 2 tanα.cotα = 4 – 2 = 2.
Vậy tan3 α + cot3 α = -2 và đáp án là C.
Đáp án: C
Câu 14:
Cho sinα = √5/4. Giá trị cos(α + π/2) là
Xem đáp án
Cách 1
Ta có sinα > 0 nên
k2π < α < π + k2π, k ∈ Z ⇒ π/2 + k2π < α + π/2 < 3π/2 + k2π.
Do đó cos(α+ π/2) < 0, nên các phương án B, C bị loại. Mặt khác cos(α+ π/2) > -1 nên phương án A bị loại. Vậy đáp án là D.
Cách 2. Ta có
cos(α+ π/2) = cos(α- π/2+ π) = - cos(α- π/2).
Vậy đáp án là D.
Đáp án: D
Câu 15:
Cho sinα = √6/3. Giá trị của biểu thức
Xem đáp án
Cách 1. Suy luận.
Tử số của P lớn hơn hoặc bằng 2, còn mẫu số là sin2 a. cos2 a = 2/3. 1/3 = 2/9 < 1/4, nên P ≤ 8. Do đó các phương án A, B, D bị loại. Đáp án là C.
Cách 2. Tính trực tiếp.
sina = √6/3 ⇒ sin2 a = 2/3 ⇒ cos2 a = 1/3.
Vậy tan2 a = 2, cot2 a = 1/2.
Do đó P = 45/4. Đáp án là C.
Đáp án: C