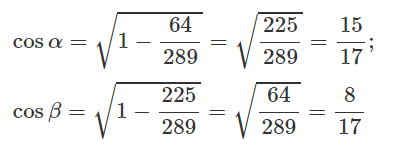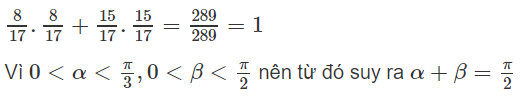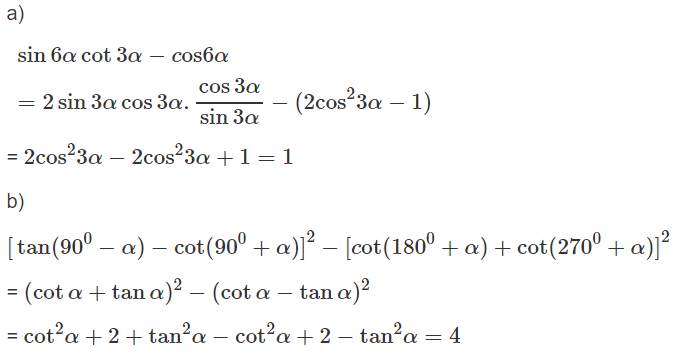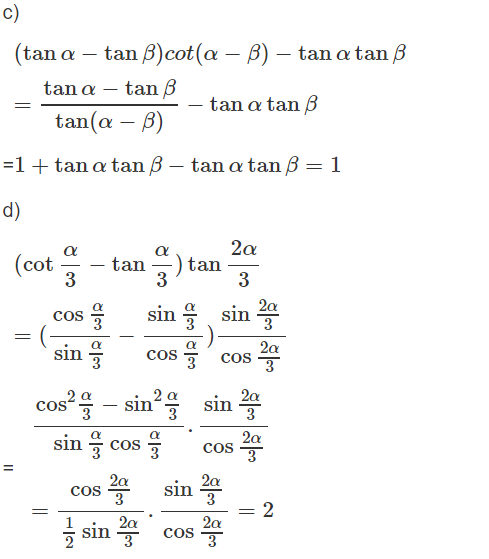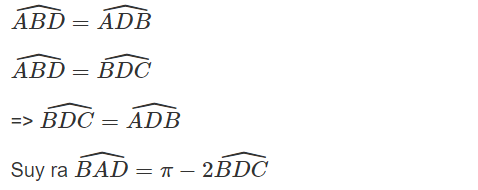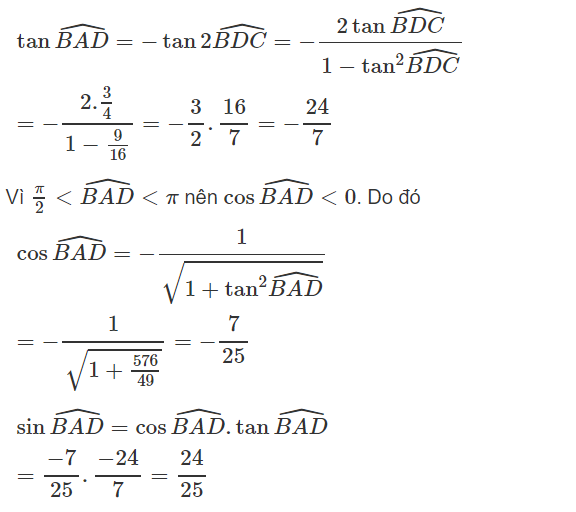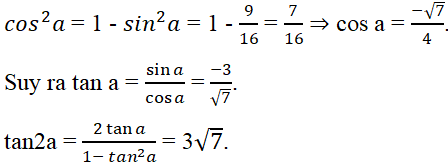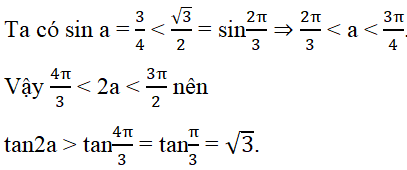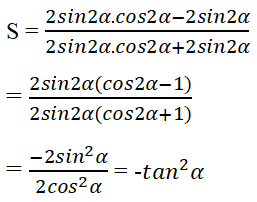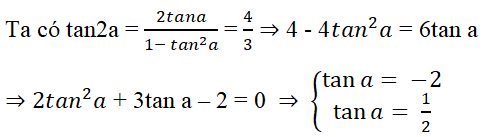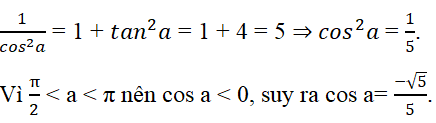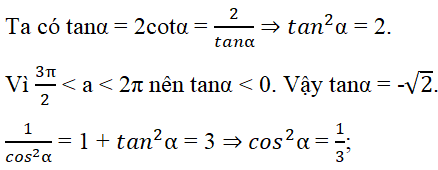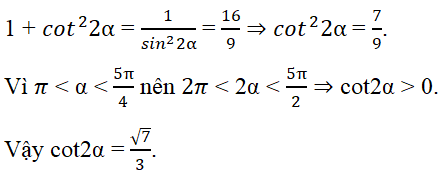12 câu hỏi trắc nghiệm thuộc Bài 3: Công thức lượng giác - SBT Đại số 10

Giải SBT Toán 10 Đại số - Chương 6: Cung và góc lượng giác. Công thức lượng giác

Bài 3: Công thức lượng giác - SBT Đại số 10

2146 lượt thi
12 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho cosα = 1/3, tính sin(α + π/6) - cos(α - 2π/3)

Xem đáp án

Câu 2:

Cho sinα = 8/17, sinβ = 15/17 với 0 < α < π/2, 0 < β <π/2. Chứng minh rằng: α + β = π/2

Xem đáp án

Ta có:

Do đó: sin(α + β) = sinαcosβ + cosαsinβ

Câu 3:

Chứng minh rằng các biểu thức sau là những hằng số không phụ thuộc α, β

a) sin6αcot3α - cos6α;

b) [tan(90^ο - α) - cot(90^ο + α)]² - [cot(180^ο + α) + cot(270^ο + α)]² ;

c) (tanα - tanβ)cot(α - β) - tanαtanβ;

d) (cot α/3 - tanα/3) tan2α/3

Xem đáp án

Câu 4:

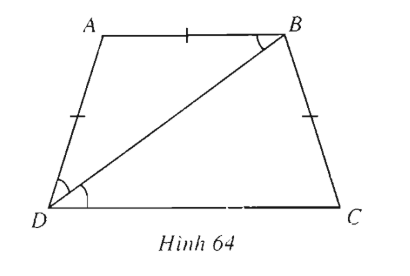
Cho hình thang cân ABCD có đáy nhỏ AB = AD. Biết tanBDC = 3/4, tính các giá trị lượng giác của BAD.

Xem đáp án

Ta có (h.64)

Từ đó ta có:

Câu 5:

Nếu sinα = 2/√5 thì cos2α bằng

A. 0,5

B. -0,25

C. 3/√5

D. -0,6

Xem đáp án

Ta có cos2α = 1 - 2sin² α = 1 - 8/5 = (-3)/5 = -0,6.

Đáp án: D

Câu 6:

Biết sina + cosa = √2/2. Giá trị sin2a là

A. 2√2/3

B. -2/3

C. -1/2

D. 1/2

Xem đáp án

Ta có (sina + cosa)² = 1 + sin2a ⇒ 1/2 = 1 + sin2a. Vậy sin2a = (-1)/2

Đáp án: C

Câu 7:

Cho π/2 < a < 3π/4. Giá trị tan2a là

A. -2√7

B. 3√3/4

C. -3√7

D. 3√7

Xem đáp án

Cách 1. Tính trực tiếp.

Với π/2 < a < 3π/4 thì cosa < 0. Ta có

Đáp án là D.

Cách 2. Suy luận.

Do đó các phương án A, B, C bị loại.

Đáp án: D

Câu 8:

Cho 0 < α < π/2. Biểu thức $S = \frac{\sin 4 α - 2 \sin 2 α}{\sin 4 α + 2 \sin 2 α}$ có thể rút gọn thành biểu thức nào sau đây?

A. -tan2α

B. tanα

C. cot2α

D. cotα

Xem đáp án

Đáp án: A

Ta cũng có thể suy luận cos2α – 1 < 0, cos2α + 1 > 0 nên S < 0, do đó các phương án B, C, D bị loại. Vậy đáp án là A.

Câu 9:

Cho tan2a = 4/3 với π/2 < a < π. Giá trị cos a là

A. $\frac{- \sqrt{5}}{5} hoặc \frac{2 \sqrt{5}}{5}$

B. $\frac{- \sqrt{5}}{5}$

C. $\frac{\sqrt{5}}{5} hoặc \frac{- 2 \sqrt{5}}{5}$

D. $\frac{\sqrt{5}}{5}$

Xem đáp án

Cách 1. Tính trực tiếp.

Vì π/2 < a < π nên tan a < 0, do đó tan a = -2.

Áp dụng công thức

Đáp án là B.

Cách 2. Suy luận

Vì π/2 < a < π nên cos a < 0, do đó các phương án A, C, D bị loại.

Đáp án: B

Câu 10:

Biết sina = -4/5 với 3π/4 < a < π. Giá trị tan a là

A. 1/2

B. 2

C. -2

D. -1/2

Xem đáp án

Cách 1. Tính trực tiếp.

Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.

Cách 2. Suy luận

Với 3π/4 < a < π thì -1 < tan a < 0, nên các phương án A, B, C đều bị loại.

Đáp án: D

Câu 11:

Cho tanα = 2cotα và 3π/2 < α < 2π. Giá trị của biểu thức sinα + cosα là

A. $\frac{\sqrt{6} - \sqrt{3}}{3}$

B. $\frac{\sqrt{3} - \sqrt{6}}{3}$

C. $\frac{2 - \sqrt{3}}{3}$

D. $\frac{2 + \sqrt{3}}{3}$

Xem đáp án

Cách 1. Tính trực tiếp

Do đó cosα = √3/3 (vì cosα > 0).

Suy ra sinα = tanα.cosα = (-√6)/3.

Vậy sinα + cosα = (√3- √6)/3. Đáp án là B.

Cách 2. Suy luận

Vì tanα = 2cotα và 3π/2 < α < 2π nên 3π/2 < α < 7π/4.

Do đó sinα < (-√2)/2 và cosα < √2/2.

Vì vậy sinα + cosα < 0.

Suy ra các phương án A, C, D bị loại.

Đáp án: B

Câu 12:

Biết sinα - cosα = 1/2 và π < α < 5π/4. Giá trị cot2α là

A. $\frac{- \sqrt{7}}{3}$

B. $\frac{1 - \sqrt{5}}{3}$

C. $\frac{2 - \sqrt{7}}{3}$

D. $\frac{\sqrt{7}}{3}$

Xem đáp án

Cách 1. Tính trực tiếp

Ta có (sinα – cosα)² = 1/4 = 1 – sin2α ⇒ sin2α = 3/4.

Đáp án là D.

Cách 2. Suy luận

Vì π < α < 5π/4 nên 2π < 2α < 5π/2. Suy ra cot2α > 0.

Do đó các phương án A, B, C đều bị loại.

Đáp án: D

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Đại số - Chương 6: Cung và góc lượng giác. Công thức lượng giác

Bài 3: Công thức lượng giác - SBT Đại số 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương