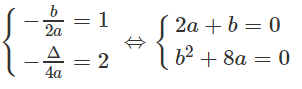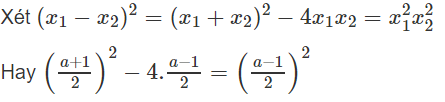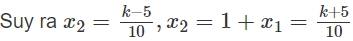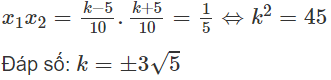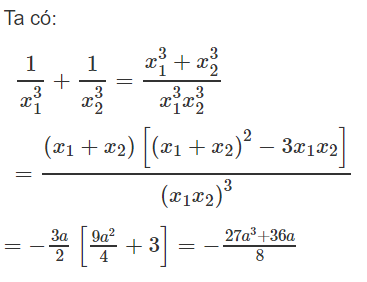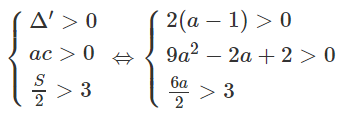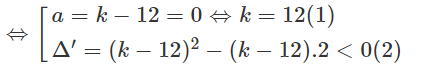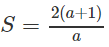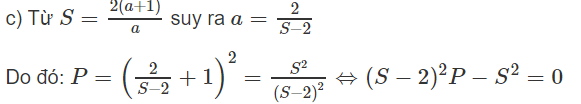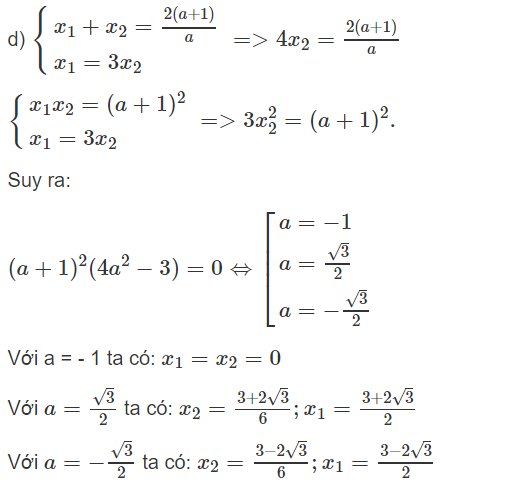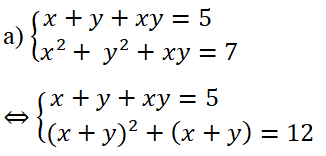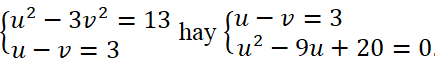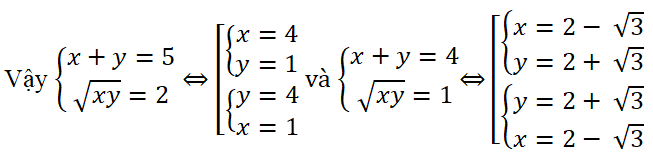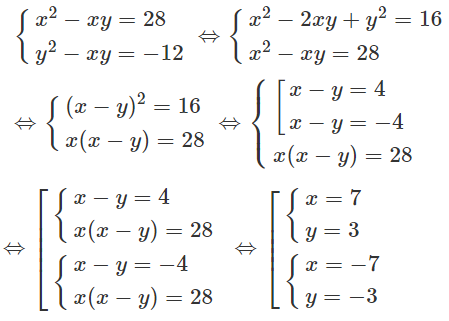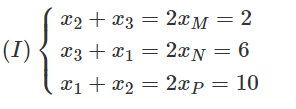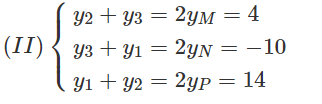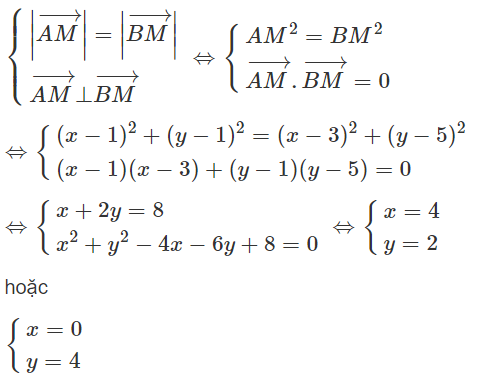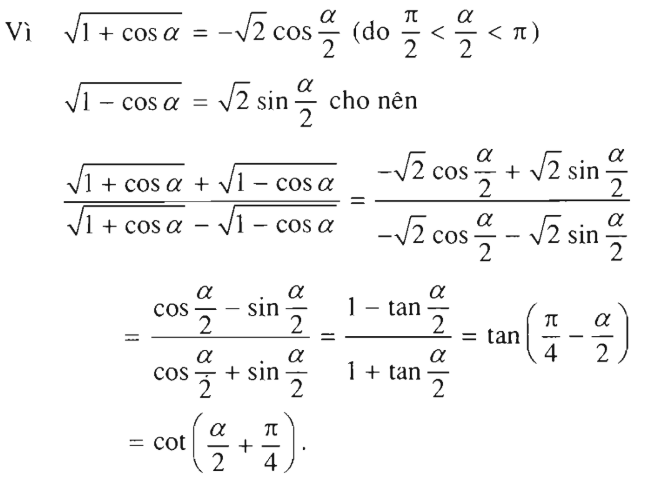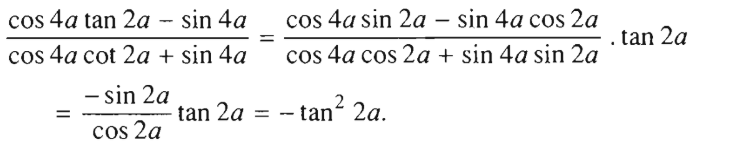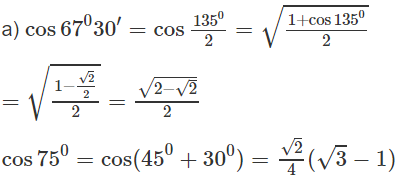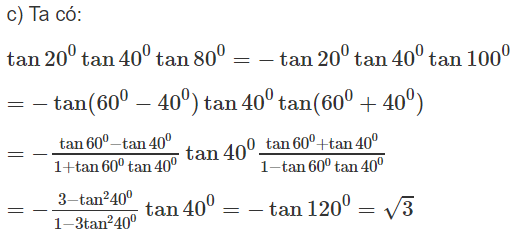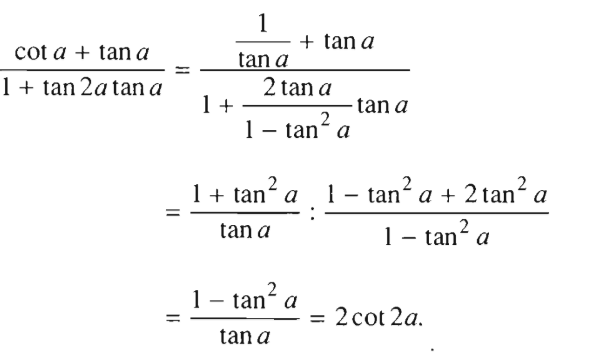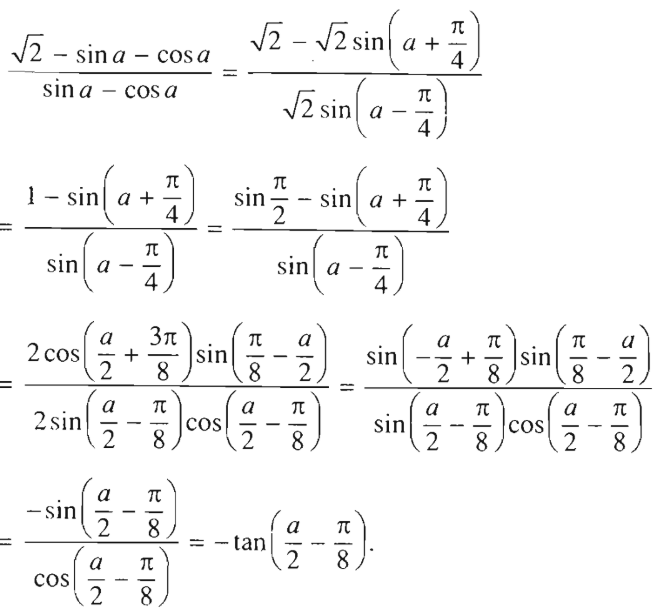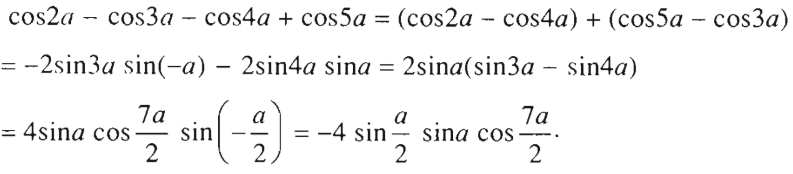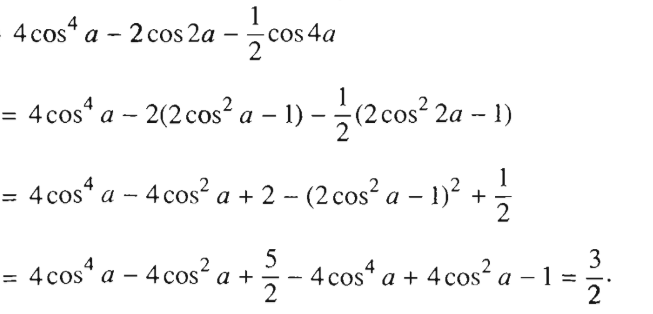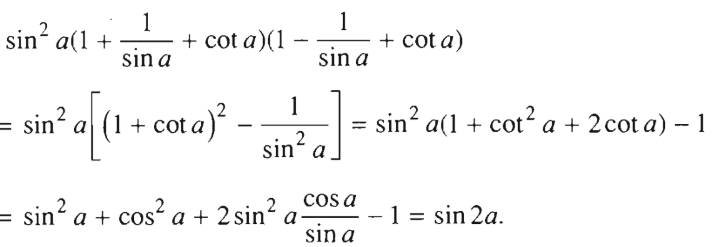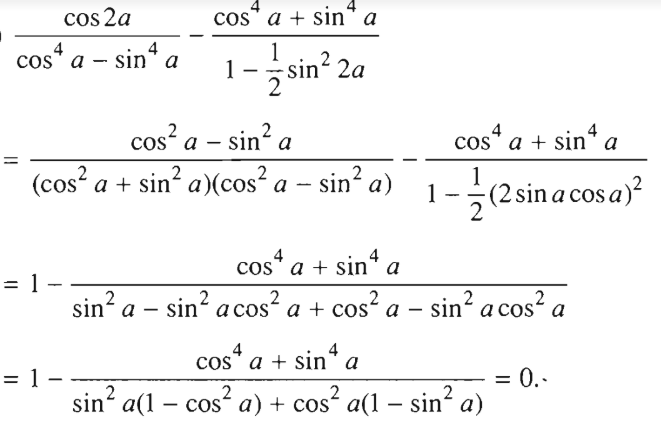35 câu hỏi trắc nghiệm thuộc Ôn tập cuối năm - SBT Đại số 10

Câu 1:

Xác định parabol y = ax² + bx + c trong mỗi trường hợp sau

a) Parabol nhận trục tung làm trục đối xứng và cắt đường thẳng y = x/2 tại các điểm có hoành độ là -1 và 3/2

b) Parabol đi qua gốc tọa độ và có đỉnh là điểm (1;2).

c) Parabol đi qua hai điểm A(-1; 2), B(2; 3) và có trục đối xứng là đường thẳng x = 1.

Xem đáp án

a) Vì đồ thị nhận trục tung làm trục đối xứng cho nên hàm số f(x) = ax² + bx + c là hàm số chẵn, do đó

f(x) = ax² + bx + c = ax² - bx + c = f(-x), ∀x

Suy ra b = 0. Ta còn phải xác định a và c.Suy ra b = 0. Ta còn phải xác định a và c.

Vì parabol cắt đường thẳng y = x/2 tại các điểm có hoành độ -1 và 3/2 nên nó đi qua các điểm (-1; -1/2) và (3/2; 3/4)

Ta có hệ phương trình

Giải hệ phương trình trên ta được a = 1; c = -3/2

Parabol phải tìm là y = x² - 3/2

b) Vì parabol đi qua (0;0) nên y(0) = c = 0.

Do parabol có đỉnh là (1 ; 2) nên

Giải hệ phương trình trên ta được a = -2, b = 4.

Parabol phải tìm là y = -2x² + 4x

c) a = -1/3, b = 2/3, c = 3

Câu 2:

Với những giá trị nào của a, hiệu giữa hai nghiệm của phương trình

2x² - (a + 1)x + (a - 1) = 0

Bằng tích của chúng?

Xem đáp án

Ta có: Δ = (a + 1)² - 8(a - 1)= a² + 2a + 1 - 8a + 8

a² - 6a + 9 = (a - 3)² ≥ 0 nên phương trình đã cho có nghiệm

⇔ -4a + 8 = 0 ⇔ a = 2

Đáp số: a = 2

Câu 3:

Hãy xác định k để hiệu giữa các nghiệm của phương trình 5x² - kx + 1 = 0 bằng 1

Xem đáp án

Cần có: Δ = k² - 20 > 0

Xét x₁ - x₂ = (x₁ + x₂) - 2x₂ = 1 ⇒ k/5 - 2x₂ = 1

Do đó

Câu 4:

Tìm các giá trị của a sao cho tổng các nghiệm của phương trình x₂ - 2a(x - 1) - 1 = 0 bằng tổng bình phương các nghiệm đó

Xem đáp án

x₂ - 2a(x - 1) - 1 = 0 ⇔ x² - 2ax + 2a - 1 = 0

Vì Δ' = (a - 1)² ≥ 0 nên phương trình luôn có nghiệm

Ta có: x₁ + x₂ = 2a

x₁. x₂ = 2a - 1

x₁² + x₂² = (x₁ + x₂)² - 2x₁x₂

Suy ra 4a² - 2(2a - 1) = 2a ⇔ 2a² - 3a + 1 = 0

Giải phương trình trên ta được a = 1/2; a = 1

Đáp số: a = 1/2; a = 1

Câu 5:

Tính $\frac{1}{x_{1}^{3}} + \frac{1}{x_{2}^{3}}$ trong đó x₁ và x₂ là các nghiệm của các phương trình bậc hai 2x² - 3ax - 2 = 0.

Xem đáp án

Câu 6:

Tìm giá trị của a sao cho phương trình x² - 6ax + 2 - 2a + 9a² = 0 Có hai nghiệm dương phân biệt và đều lớn hơn 3.

Xem đáp án

Phải có

Giải hệ bất phương trình trên ta được a > 1.

Câu 7:

Tìm các giá trị nguyên của k sao cho phương trình: (k - 12)x² + 2(k - 12)x + 2 = 0 vô nghiệm

Xem đáp án

Phương trình: (k - 12)x² + 2(k - 12)x + 2 = 0 vô nghiệm

Xét (2):

Đặt k - 12 = t ⇒ t² - 2t < 0 ⇔ 0 < t < 2

Vậy: 0 < k - 12 < 2 ⇔ 12 < k < 14, mà k nguyên ⇒ k = 13 (3)

Từ (1) và (3) ⇒ k = 12, k = 13

Câu 8:

Cho phương trình bậc hai

ax² - 2(a + 1)x + (a + 1)²a = 0 (E)

Kí hiệu S là tổng, P là tích các nghiệm (nếu có) của phương trình trên.

a) Với giá trị nào của a, phương trình (E) có nghiệm?

b) Biện luận dấu của S và P. Từ đó suy ra dấu các nghiệm của (E).

c) Tìm hệ thức giữa S và P độc lập đối với a.

d) Với những giá trị nào của a, các nghiệm x₁, x₂ của (E) thỏa mãn hệ thức x₁ = 3x₂? Tìm các nghiệm x₁, x₂ trong mỗi trường hợp đó.

Xem đáp án

a) Phải có:

Δ = (a + 1)² - (a + 1)²a² = (a + 1)²(1 - a²) ≥ 0

⇔ -1 ≤ a ≤ 1, a ≠ 0

b) Ta có:

P = (a + 1)²

P = 0 ⇔ a = -1, khi đó x₁ = x₂ = 0

P > 0, ∀a ≠ -1 khi đó x₁, x₂ cùng dấu.

Mặt khác

Suy ra:

Với 0 < a ≤ 1 thì hai nghiệm của phương trình (E) đều dương;

Với -1 ≤ a < 0 thì hai nghiệm của phương trình (E) đều âm;

Câu 9:

Giải và biện luận các hệ phương trình sau

a) (1) $\{\begin{cases} x + ay = 1 \\ ax + y = 2 a \end{cases}$

b) (2) $\{\begin{cases} ax + y = a \\ x + ay = a^{2} \end{cases}$

Xem đáp án

a) Với a ≠ 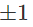hệ phương trình (1) có nghiệm

Với a = 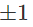hệ phương trình (1) vô nghiệm.

b) Nếu a ≠ 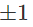thì thì x = 0, y = a;

Nếu a = -1 thì x = t + 1, y = 1 (t ∈ R)

Nếu a = 1 thì x = t, y = 1 - t (t ∈ R)

Câu 10:

Giải các hệ phương trình sau

$A . \{\begin{cases} a + y + xy = 5 \\ x^{2} + y^{2} + xy = 7 \end{cases} B . \{\begin{cases} x^{2} + y^{2} - xy = 13 \\ x + y - \sqrt{xy} = 3 \end{cases}$

Xem đáp án

Đặt u = x + y ta được u² + u – 12 = 0.

Giả ra ta được u₁ = 3, u₂ = -4.

Với u = 3 ta có hệ phương trình (*)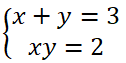

Giải hệ phương trình (*) ta được hai nghiệm (1;2) và (2;1).

Với u = -4 ta có hệ phương trình 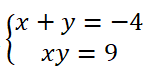(vô nghiệm)

Đáp số: (1;2) và (2;1)

b) Đặt 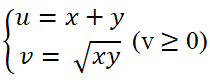ta được hệ phương trình

Giải hệ phương trình trên ta được: u = 5, v = 2 hoặc u = 4, v = 1

Câu 11:

Giải các hệ phương trình sau

a) $\{\begin{cases} x^{2} - xy = 28 \\ y^{2} - xy = - 12 \end{cases}$

b) $\{\begin{cases} 5 (x + y) + 2 xy = - 19 \\ 15 xy + 5 (x + y) = - 175 \end{cases}$

Xem đáp án

a)

b)

Câu 12:

Trong mặt phẳng tọa độ Oxy, tìm tọa độ các đỉnh của tam giác ABC, biết tọa độ trung điểm của các cạnh BC, CA, AB lần lượt là M(1;2), N(3;-5), P(5; 7).

Xem đáp án

Giả sử các đỉnh của tam giác có tọa độ lần lượt là

A(x₁, y₁), B(x₂, y₂), C(x₃, y₃)

Theo công thức tọa độ trung điểm ta có:

và

Cộng từng vế các phương trình của hệ (I) ta được

2(x₁ + x₂ + x₃) = 18 ⇒ x₁ + x₂ + x₃ = 9

từ đó: x₁ = 7; x₂ = 3; x₃ = -1

Tương tự tìm được: y₁ = 0; y₂ = 14; y₃ = -10

Vậy A(7; 0); B(3; 14); C(-1; -10).

Câu 13:

Trong mặt phẳng tọa đọ Oxy hãy tìm tọa độ các đỉnh M, N của hình vuông AMBN, biết tọa độ hai đỉnh A(1; 1) và B(3; 5).

Xem đáp án

Giả sử M(x; y) là đỉnh của hình vuông AMBN.

Ta có:

Vậy M(4; 2), N(0; 4) hoặc M(0; 4), N(4; 2).

Câu 14:

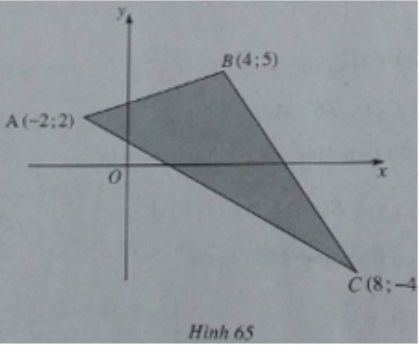
Biểu diễn hình học tập nghiệm của hệ bất phương trình

$\{\begin{cases} 2 y - x \leq 6 \\ 9 y + 4 \leq 56 \\ 3 x + 5 y \geq 4 \end{cases}$

Xem đáp án

(h.65) Tập nghiệm là miền tam giác ABC (kể cả biên).

Câu 15:

Cho các số liệu thống kê ghi trong bảng sau

Thời gian giải xong một bài tập Toán của 44 học sinh lớp 10A, trường Trung học phổ thông K

23,5	23,0	21,1	23,7	23,2	21,9	24,0	22,7
19,6	22,5	22,3	20,0	23,2	21,5	20,1	23,7
20,6	24,6	22,3	21,0	25,4	22,7	21,3
21,2	23,6	23,1	21,6	24,2	22,6	22,0
22,7	19,8	23,2	21,9	20,3	22,6	22,2
21,1	20,5	24,8	22,5	20,9	25,0	23,3

a) Lập bảng phân bố tần số và tần suất ghép lớp với các lớp như sau:

[19,5; 20,5); [20,5; 21,5); [21,5; 22,5); [22,5; 23,5); [23,5; 24,5); [24,5; 25,5].

b) Dựa vào bảng phân bố tần suất ghép lớp đã lập hãy nêu nhận xét về thời gian làm một bài tập của 44 học sinh kể trên.

c) Hãy tính số trung bình cộng x−, phương sai s_x²và độ lệch chuẩn s_xcủa các số liệu thống kê đã cho.

d) Giải sử rằng, cũng khảo sát thời gian giải xong một bài tập Toán của học sinh ở các lớp 10B, 10C của trường K, rồi tính các số trung bình cộng, phương sai và độ lệch chuẩn của các số liệu thống kê ở từng lớp, ta thu được kết quả sau:

Ở lớp 10B có y− = 20 phút, s_y² = 1; s_y = 1 phút

Ở lớp 10C có z− = 20 phút, s_z² = 1; s_z = 1 phút

Hãy so sánh thời gian giải xong một bài tập Toán của học sinh ở ba lớp 10A, 10B, 10C đã cho.

e) Vẽ biểu đồ tần suất hình cột mô tả bảng phân bố tần suất ghép lớp đã lập được.

Xem đáp án

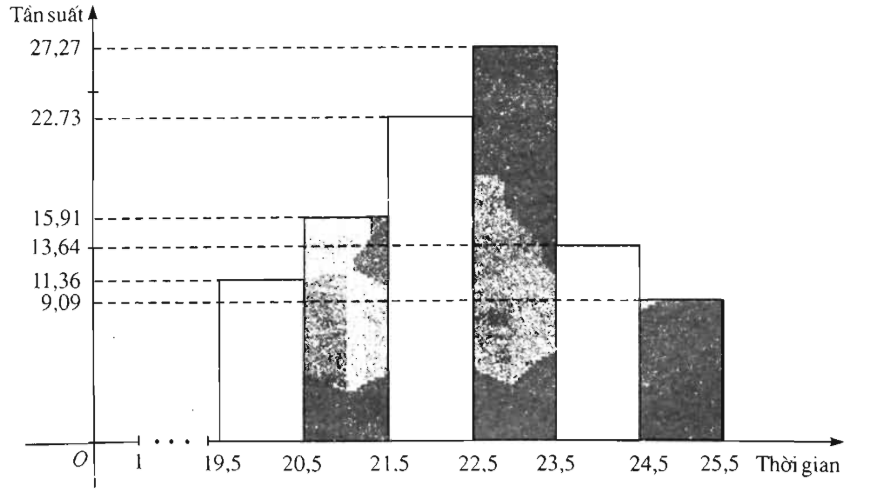
a) Thời gian giải xong một bài tập toán của 44 học sinh lớp 10A, trường Trung học phổ thông K

Lớp thời gian (phút)	Tần số	Tần suất (%)
[19,5;20,5)	5	11,36
[20,5; 21,5)	7	15,91
[21,5; 22,5)	10	22,73
[22,5; 23,5)	12	27,27
[23,5; 24,5)	6	13,64
[24,5; 25,5]	4	9,09
Cộng	44	100 (%)

b) Nhận xét:

Trong 44 học sinh đã được khảo sát ta thấy:

Chiểm tỉ lệ thấp nhất (9,09%) là những học sinh có thời gian giải xong một bài tập toán từ 24,5 phút đến 25,5 phút.

Chiểm tỉ lệ cao nhất (27,27%) là những học sinh có thời gian giải xong một bài tập toán từ 22,5 phút đến dưới 23,5 phút.

Đa số (79,55%) là những học sinh có thời gian giải xong bài tập toán đó từ 20,5 phút đến dưới 24,5 phút.

c) Sử dụng bảng phân bố tần số ghép lớp đã lập, ta tính được x− = 22,4 phút, s_x² = 2,1, s_x = 1,4 phút

d) x− ≈ z− = 22,4 phút > 20 phút = y− và s₁² = 2,1 > 1 = s_z²nên thời gian giải xong bài tập toán đó của các học sinh lớp 10C là đồng đều hơn các học sinh lớp 10A.

e) Biểu đồ tần suất hình cột về thời gian (phút) giải xong một bài tập toán của 44 học sinh lớp 10A, trường Trung học phổ thông K (h.66)

Câu 16:

a) $\frac{\sqrt{1 + cosα} + \sqrt{1 - cosα}}{\sqrt{1 + cosα} - \sqrt{1 - cosα}} = \cot (\frac{α}{2} + \frac{π}{4})$

b) $\frac{\cos 4 α \tan 2 α - \sin 4 α}{\cos 4 α \cot 2 α + \sin 4 α} = - \tan^{2} 2 a$

c) $1 + 2 \cos 7 α = \frac{\sin 10, 5 α}{\sin 3, 5 α}$

d) $\frac{\tan 3 α}{tanα} = \frac{3 - \tan^{2} α}{1 - 3 \tan^{2} α}$

Xem đáp án

a)

b)

c)

d)

Câu 17:

Rút gọn

a) $\frac{\sin^{2} 2 α + 4 \sin^{4} α - 4 \sin^{2} α \cos^{2} α}{4 - \sin^{2} 2 α - 4 \sin^{2} α}$

b) $3 - 4 \cos 2 a + \cos 4 a$

c) $\frac{cotα + tanα}{1 + \tan 2 αtanα}$

Xem đáp án

c)

Câu 18:

Không dùng bảng số và máy tính, hãy tính

a) cos67^ο30' và cos75^ο

b) $\frac{\cot 15^{o} + 1}{2 \cot 15^{o}}$

c) tan20^οtan40^οtan80^ο

Xem đáp án

b)

Câu 19:

Chứng minh rằng:

a) $\frac{cota + tana}{1 + \tan 2 tana} = 2 \cot 2 a$

b) $\frac{\sqrt{2} - sina - cosa}{sina - cosa} = - \tan (\frac{a}{2} - \frac{π}{8})$

c) $\cos 2 a - \cos 3 a - \cos 4 a + \cos 5 a = - 4 \sin \frac{a}{2} sinacos \frac{7 a}{2}$

Xem đáp án

a)

b)

c)

Câu 20:

Rút gọn

a) $4 \cos^{4} a - 2 \cos 2 a - \frac{1}{2} \cos 4 a$

b) $\sin^{2} a (1 + \frac{1}{sina} + cota) (1 - \frac{1}{sina} + cota)$

c) $\frac{\cos 2 a}{\cos^{4} a - \sin^{4} a} - \frac{\cos^{4} a + \sin^{4} a}{1 - \frac{1}{2} \sin^{2} 2 a}$

Xem đáp án

a)

b)

c)

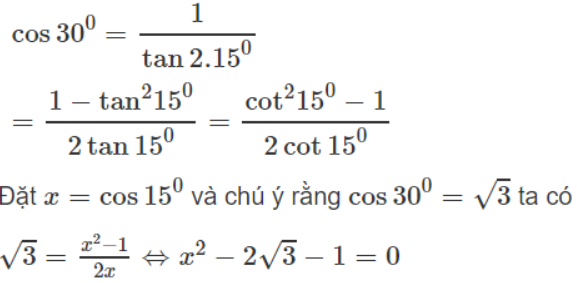
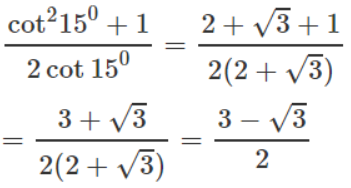
Câu 21:

Tìm k sao cho phương trình sau đây có nghiệm kép: x² + kx + 2k = 0.

A. k = 0; k = 8

B. k = 8

C. k = 10; k = 2

D. k = 0; k = 1

Xem đáp án

Giả Δ = 0

Đáp án: A

Câu 22:

Cho phương trình kx² + (k + 5)x + k + 8 = 0.

Xác định k để phương trình có một nghiệm bằng -1

A. k = 1

B. k = -3

C. k = 2

D. k = 5

Xem đáp án

Thay x = -1 vào phương trình.

Đáp án: B

Câu 23:

Tính giá trị biểu thức $\cos \frac{π}{7} \cos \frac{4 π}{7} \cos \frac{5 π}{7}$

A. 1/8

B. -1/8

C. 1/5

D. 2/5

Xem đáp án

Nhân biểu thức đã cho với sinπ/7.

Đáp án: A

Câu 24:

Giá trị của biểu thức cos4a - sin4a.cot2a là:

A. 1/2

B. -1

C. -1/3

D. -2

Xem đáp án

Áp dụng công thức cotx = cos⁡x/sin⁡x và cos2x = 2cos²x – 1.

Đáp án: B

Câu 25:

Cho phương trình: 3x² - 5x - 2 = 0

Tổng bình phương các nghiệm của nó là:

A. 13/25

B. 4/15

C. 37/9

D. 25/9

Xem đáp án

x₁ ² + x₂ ² = (x₁ + x₂ )² - 2x₁ x₂ = 37/9.

Đáp án: C

Câu 26:

Cho phương trình x² - 3x + 2 = 0, hãy tính tổng lập phương các nghiệm của nó.

A. 11

B. 15

C. 7

D. 9

Xem đáp án

x₁ ³ + x₂ ³ = (x₁ + x₂ )( x₁ ² - x₁ x₂ + x₂ ²)

= (x₁ + x₂ )[ (x₁ + x₂ )²-3x₁ x₂ ] = 9.

Đáp án: D

Câu 27:

Với giá trị nào của tham số m, hệ phương trình $\{\begin{cases} 3 x + my = 3 \\ mx + 3 y = 3 \end{cases}$ có vô số nghiệm?

A. m = 2

B. m = 3

C. m = 4

D. m = 5

Xem đáp án

Đáp án: B

Câu 28:

Biểu thức $\frac{1 + cosα}{1 - cosα} . \tan^{2} \frac{α}{2} - \cos^{2} α$ bằng:

A. $\cos^{2} a$

B. $\sin^{2} a$

C. $\tan^{2} a$

D. $\cot^{2} a$

Xem đáp án

Đáp án: B

Câu 29:

Tập nghiệm của bất phương trình 3x² - 7x + 4 ≤ 0 là:

A. [1; 4/3]

B. (-∞; 1)

C. (4/3; +∞)

D. Z

Xem đáp án

Phương trình 3x^2 – 7x + 4 = 0 có hai nghiệm 1 và 4/3. Phần đồ thị của parabol y = 3x^2 – 7x + 4 ở giữa khoảng (1; 4/3) nằm dưới trục hoành.

Đáp án: A

Câu 30:

Tập nghiệm của bất phương trình x² - 3x + 5 > 0 là

A. (-∞; 2)

B. (0; +∞)

C. (-∞; +∞)

D. ∅

Xem đáp án

Vì x^2 – 3x + 5 = (x- 3/2)^2 + 11/4 > 0 ∀x ∈ R.

Đáp án: C

Câu 31:

Tìm m để parabol (P) y = x² - 4x + 3 + m đi qua điểm M(1; 3)

A. m = -5

B. m = 1

C. m = 2

D. m = 3

Xem đáp án

(P) đi qua điểm M(1;3) ⇒ 3 = 1 – 4 + 3 + m ⇒ m = 3.

Đáp án: D

Câu 32:

Tìm tất cả các giá trị của m để phương trình (m - 3)x + 2 - 3m = 0 có nghiệm.

A. m ≠ 2

B. m = 2

C. m ≠ 3

D. m = 4

Xem đáp án

Đáp án: C

Câu 33:

Cho đường thẳng (d): y = (m - 1)x + 3; (d'): y = (2 - m)x - 4

A. m = 3/2

B. m = 2/3

C. m = 1

D. m = -2

Xem đáp án

Đáp án: A

Câu 34:

Tính sin75^ο.

A. $\frac{\sqrt{3}}{2} (\sqrt{2} - 1)$

B. $\frac{\sqrt{2}}{4} (\sqrt{3} + 1)$

C. $\frac{\sqrt{3}}{2} - 1$

D. $\frac{\sqrt{2} + 1}{2}$

Xem đáp án

Đáp án: B

Câu 35:

Biểu thức $\frac{1 - \cos 2 α + \sin 2 α}{1 + \cos 2 α + \sin 2 α}$ bằng:

A. cos a

B. sin a

C. tan a

D. cot a

Xem đáp án

Đáp án: C

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Đại số - Chương 6: Cung và góc lượng giác. Công thức lượng giác

Ôn tập cuối năm - SBT Đại số 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương