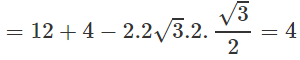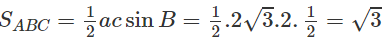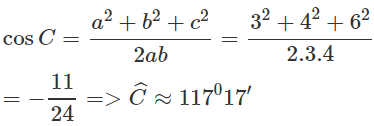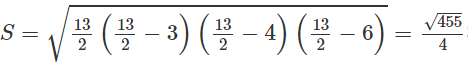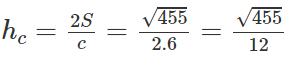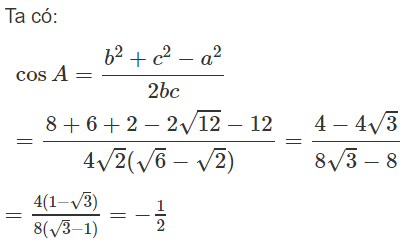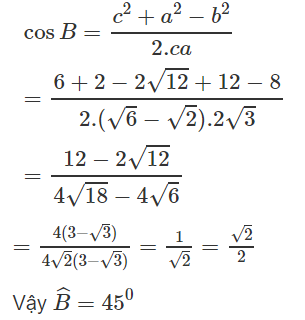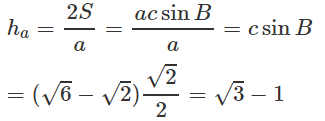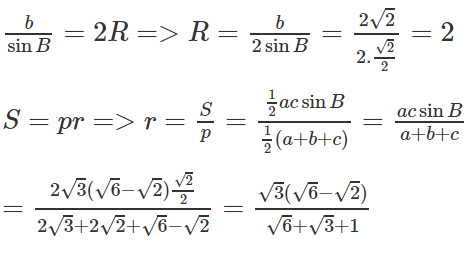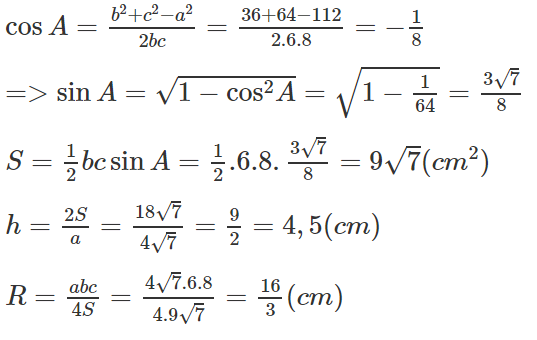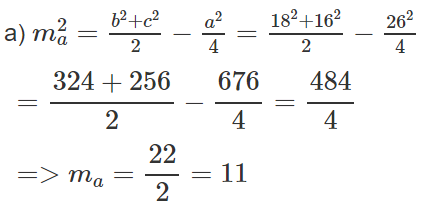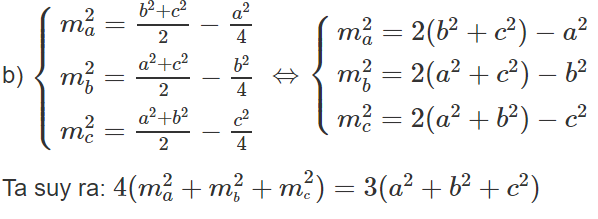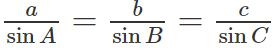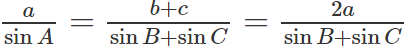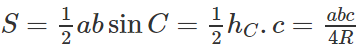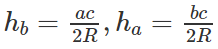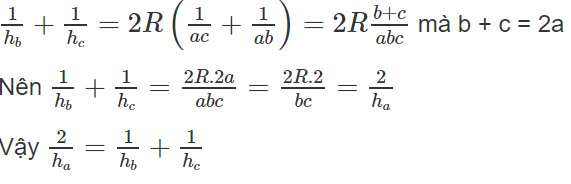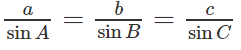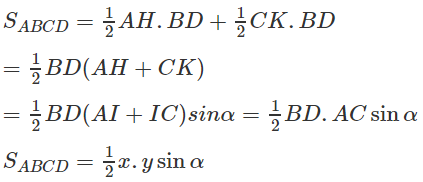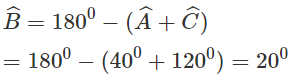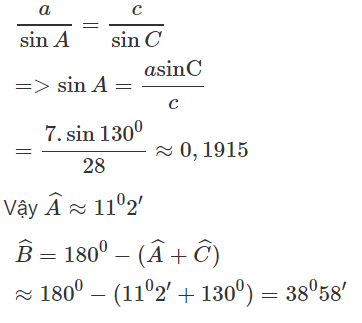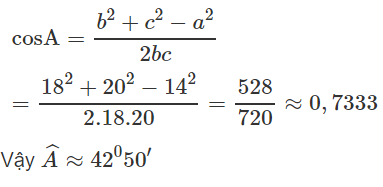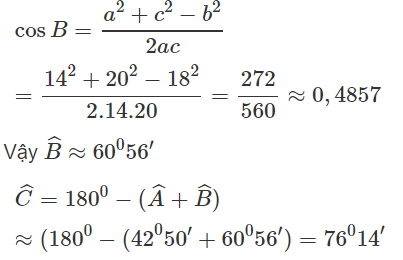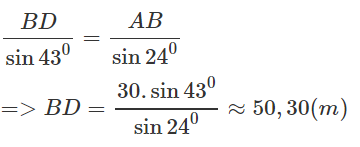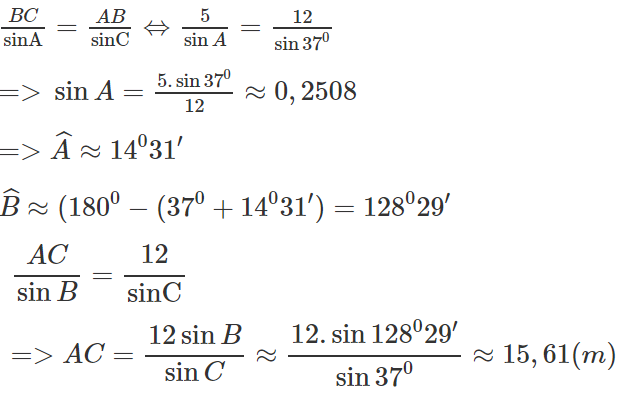Bài 3: Các hệ thức lượng trong tam giác và giải tam giác - SBT Hình học 10
-
3856 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tam giác ABC có cạnh a = 2√3, b = 2 và góc C = 30ο
a) Tính cạnh c, góc A và diện tích S của tam giác ABC;
b) Tính chiều cao ha và đường trung tuyến ma của tam giác ABC.
Xem đáp án
a) Theo định lí cô sin ta có:
c2 = a2 + b2 - 2ab cosC
Vậy c = 2 và tam giác ABC cân tại A có b = c = 2.
Ta có: C = 30ο, vậy B = 30ο và A = 180ο - (30ο + 3ο) = 120ο
Vì tam giác ABC cân tại A nên ha = ma = 1
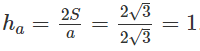
Câu 2:
Tính góc lớn nhất của tam giác ABC biết a = 3, b = 4, c = 6. Tính đường cao ứng với cạnh lớn nhất của tam giác.
Xem đáp án
Ta có c = 6 là cạnh lớn nhất của tam giác. Do đó góc C là góc lớn nhất.
Muốn tính đường cao ứng với cạnh lớn nhất ta dùng công thức Hê – rông để tính diện tích tam giác và từ đó suy ra đường cao tương ứng.
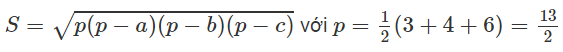
Ta có:
Câu 4:
Tam giác ABC có a = 4√7 cm, b = 6 cm, c = 8 cm. Tính diện tích S, đường cao ha và bán kính R của đường tròn ngoại tiếp tam giác đó.
Xem đáp án
Ta có:
Câu 6:
Tam giác ABC có các cạnh thỏa mãn điều kiện b + c = 2a. Chứng minh rằng:
a) 2sin A = sin B + sin C;
b)
Xem đáp án
a) Theo định lý sin ta có: 
Ta suy ra: 
⇒ 2sin A = sin B + sin C
b) Đối với tam giác ABC ta có:
Ta suy ra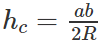 
. Tương tự ta có 
Do đó:
Câu 7:
Chứng minh rằng trong tam giác ABC ta có các hệ thức:
a) sin A = sinB.cosC + sinC.cosB
b) ha = 2R sinB. sinC
Xem đáp án
a) Theo định lý sin ta có: 
Do đó: a = 2R.sinA, b = 2R.sinB, c = 2R.sinC
Thay các giá trị này vào biểu thức: a = b.cosC + c.cosB, ta có:
2R.sinA = 2R.sinB.cosC + 2R.sinC.cosB
⇒ sin A = sinB.cosC + sinC.cosB
b) Học sinh tự chứng minh.
Câu 8:
Tam giác ABC có các cạnh thỏa mãn điều kiện bc = a2. Chứng minh rằng:
a) sin2A = sinB.sinC
b) hb.hc = h2a
Xem đáp án
a) Theo giả thiết ta có: a2 = bc
Thay a = 2R.sinA, b = 2R.sinB, c = 2R.sinC vào hệ thức trên ta có:
4R2.sin2A = 2R.sinB. 2R.sinC
⇒sin2A = sinB.sinC
b) Ta có 2S = a.ha = b.hb = c.hc
Do đó: a2. h2a = b. c. hb. hc
Theo giả thiết: a2 = bc nên ta suy ra h2a = hb.hc
Câu 9:
Chứng minh rằng diện tích hình bình hành bằng tích hai cạnh liên tiếp với sin của góc xen giữa chúng.
Xem đáp án
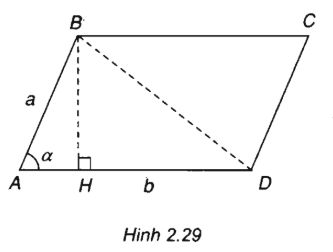
(h.2.29)
Xét hình bình hành ABCD có AB = a, AD = b, góc BAD = α và BH là đường cao, ta có BH ⊥ AD tại H
Gọi S là diện tích hình bình hành ABCD, ta có S = AD. BH với BH = ABsinα
Vậy S = AD.AB.sinα = a.b.sinα
Nếu góc BAD = α thì góc ABC = 180ο - α
Khi đó ta vẫn có sin BAD = sin ABC
Nhận xét: Diện tích hình bình hành ABCD gấp đôi diện tích
tam giác ABD mà tam giác ABD có diện tích là a.b.sinα/2.
Do đó ta suy ra diện tích của hình bình hành bằng a.b.sinα
Câu 10:
Cho tứ giác lồi ABCD có đường chéo AC = x, đường chéo BD = y và góc tạo bởi AC và BD là α. Gọi S là diện tích của tứ giác ABCD.
a) Chứng minh rằng
b) Nêu kết quả trong trường hợp AC vuông góc với BD.
Xem đáp án
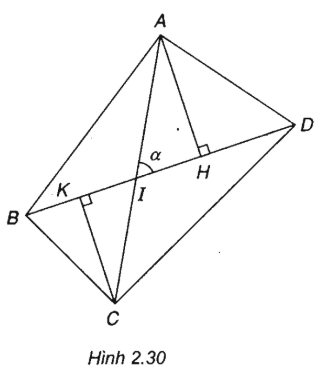
(h.2.30)
a) Ta có: SABCD = SABD + SCBD
Vẽ AH và CK vuông góc với BD.
Gọi I là giao điểm của hai đường chéo AC và BD. Ta có: AH = AI.sinα
b) Nếu AC ⊥ BD thì sinα = 1, khi đó SABCD = xy/2. Như vậy nếu tứ giác lồi ABCD có hai đường chéo AC và BD vuông góc với nhau thì diện tích của tứ giác bằng một nửa tích độ dài của hai đường chéo.
Câu 11:
Cho tứ giác lồi ABCD. Dựng hình bình hành ABDC'. Chứng minh rằng tứ giác ABCD và tam giác ACC' có diện tích bằng nhau.
Xem đáp án
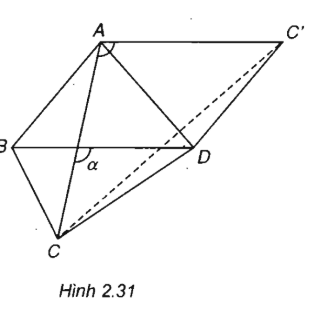
(h.2.31)
Gọi α là góc giữa hai đường chéo AC và BD của tứ giác ABCD.
Ta có: góc CAC' = α vì AC'// BD
Theo kết quả bài 2.38 ta có:
SABCD = AC.BD.sinα/2
Mặt khác: SACC' = AC.AC'.sinα/2
Mà AC' = BD nên SABCD = SACC'
Câu 12:
Cho tam giác ABC biết cạnh c = 35cm, góc A = 40ο, góc C = 120ο. Tính các cạnh a, b và góc B
Xem đáp án
Ta có:
Theo định lí sin ta có:
Câu 13:
Cho tam giác ABC biết các cạnh a = 7cm, b = 23cm, góc C = 130ο. Tính cạnh c, góc A, góc B
Xem đáp án
Theo định lí cô sin ta có:
c2 = a2 + b2 - 2ac.cosC
= 72 + 232 - 2.7.23.cos130ο ≈ 785
⇒ c ≈ 28 (cm). Theo định lí sin ta có:
Câu 14:
Cho tứ giác ABC biết a = 14cm, b = 18cm, c = 20cm. Tính góc A, B, C
Xem đáp án
Theo định lí cô sin ta có:
Câu 15:
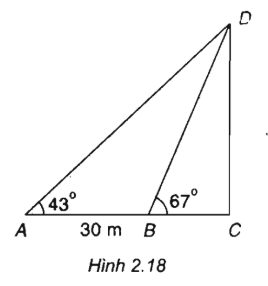
Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp, D là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm A, B có khoảng cách AB = 30 m sao cho ba điểm A, B, C thẳng hàng người ta đo được các góc CAD = 43ο, CBD = 67ο(h.2.18). Hãy tính chiều cao CD của tháp
Xem đáp án
Muốn tính chiều cao CD của tháp, trước hết ta hãy tính góc ADB
ADB = 67ο - 43ο = 24ο
Theo định lí sin đối với tam giác ABD ta có:
Trong tam giác vuông BCD ta có:
sin 67ο = CD/BD
⇒ CD = BD.sin 67ο ≈ 50,03. sin 67ο
Hay CD ≈ 46,30(m)
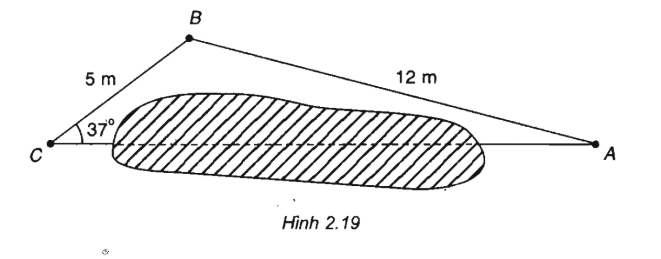
Câu 16:
Khoảng cách từ A đến C không thể đo trực tiếp vì phải qua một đầm lầy nên người ta làm như sau: Xác định một điểm B có khoảng cách AB = 12m và đo được góc ACB = 37ο (H.2.19). Hãy tính khoảng cách AC biết rằng BC = 5 m.
Xem đáp án
Theo định lí sin đối với tam giác ABC ta có:
Vậy khoảng cách AC ≈ 15.61 (m)