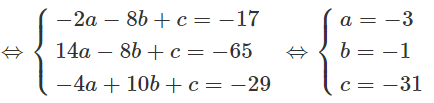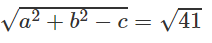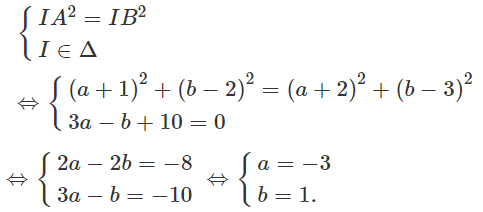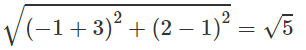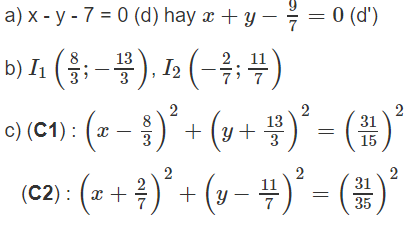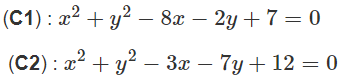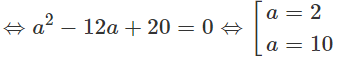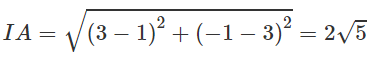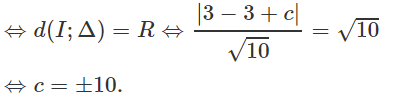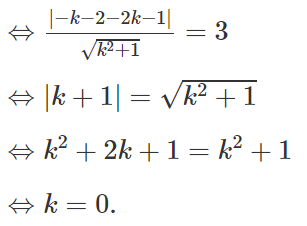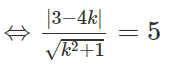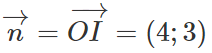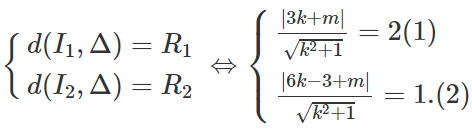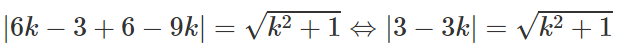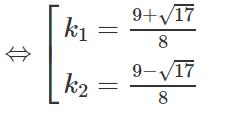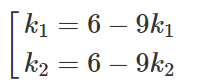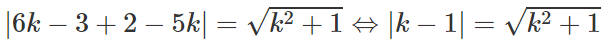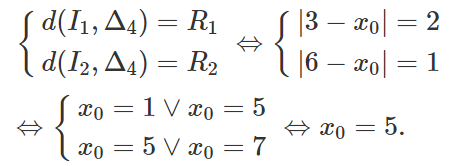Bài 2: Phương trình đường tròn - SBT Hình học 10
-
2653 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong mặt phẳng Oxy,hãy lập phương trình đường tròn (C) có tâm là điểm (2; 3) và thỏa mãn điều kiện sau:
a) (C) có bán kính là 5 ;
b) (C) đi qua gốc tọa độ ;
c) (C) tiếp xúc với trục Ox;
d) (C) tiếp xúc với trục Oy;
e) (C) tiếp xúc với đường thẳng Δ: 4x + 3y - 12 = 0.
Xem đáp án
a) (x - 2)2 + (y - 3)2 = 25;
b) (x - 2)2 + (y - 3)2 = 13;
c) (x - 2)2 + (y - 3)2 = 9;
d) (x - 2)2 + (y - 3)2 = 4;
e) (x - 2)2 + (y - 3)2 = 1.
Câu 2:
Cho ba điểm A(1; 4), B(-7; 4), C(2; -5).
a) Lập phương trình đường tròn (C) ngoại tiếp tam giác ABC ;
b) Tìm tâm và bán kính của (C).
Xem đáp án
a) Phương trình của (C) có dạng x2 + y2 - 2ax - 2by + c = 0. Ta có:
A, B, C ∈ (C)
Vậy phương trình của (C) là: x2 + y2 + 6x + 2y - 31 = 0
b) (C) có tâm là điểm (-3;-1) và có bán kính bằng
Câu 3:
Cho đường tròn tâm (C) đi qua hai điểm A(-1; 2), B(-2; 3) và có tâm ở trên đường thẳng Δ: 3x - y + 10 = 0.
a) Tìm tọa độ tâm của (C);
b) Tính bán kính R của (C);
c) Viết phương trình của (C).
Xem đáp án
Gọi I(a; b) là tâm của (C) ta có:
Vậy (C) có tâm I (-3 ; 1).
b) R = IA = 
c) Phương trình của (C) là: (x + 3)2 + (y - 1)2 = 0.
Câu 6:
Lập phương trình đường tròn bán kính AB trong các trường hợp sau:
a) A có tọa độ (-1; 1), B có tọa độ (5; 3) ;
b) A có tọa độ (-1; -2), B có tọa độ (2; 1).
Xem đáp án
a) x2 + y2 - 4x - 4y - 2 = 0
b) x2 + y2 - x + y - 4 = 0
Câu 7:
Lập phương trình của đường tròn (C) tiếp xúc với các trục tọa độ và đi qua M(4; 2).
Xem đáp án
Phương trình của (C) có dạng (x - a)2 + (y - a)2 = a2, ta có:
M ∈ (C) ⇔ (4 - a)2 + (2 - a)2 = a2
Vậy có hai đường tròn thỏa mãn đề bài là:
(x - 2)2 + (y - 2)2 = 4 và (x - 10)2 + (y - 10)2 = 100
Câu 8:
Cho đường tròn (C): x2 + y2 - x - 7y = 0 và đường thẳng d: 3x + 4y - 3 = 0.
a) Tìm tọa độ giao điểm của (C) và d.
b) Lập phương trình tiếp tuyến với (C) tại các giao điểm đó.
c) Tìm tọa độ giao điểm của hai tiếp tuyến.
Xem đáp án
a) M1(1; 0), M2(-3; 3)
b) Δ1: x - 7y - 1 = 0
Δ2: 7x + y + 18 = 0
c) A(-5/2; -1/2).
Câu 9:
Cho đường tròn (C): x2 + y2 - 6x + 2y + 6 = 0 và điểm A(1; 3)
a) Chứng tỏ rằng điểm A nằm ngoài đường tròn (C) .
b) Lập phương trình tiếp tuyến với (C) xuất phát từ điểm A.
Xem đáp án
a) (C) có tâm I (3;-1) và có bán kính R = 2, ta có:
và IA > R, vậy A nằm ngoài (C).
b) Δ1: 3x + 4y - 15 = 0
Δ2: x - 1 = 0
Câu 10:
Lập phương trình tiếp tuyến Δ của đường tròn (C): x2 + y2 - 6x + 2y = 0 biết rằng Δ vuông góc với đường thẳng d: 3x - y + 4 = 0
Xem đáp án
Δ vuông góc với d nên phương trình Δ có dạng: x + 3y + c = 0
(C) có tâm I(3;-1) và có bán kính R = √10. Ta có:
Δ tiếp xúc với (C) :
Vậy có hai tiếp tuyến thỏa mãn đề bài là:
Δ1: x + 3y + 10 = 0 và Δ2: x + 3y - 10 = 0
Câu 11:
Cho đường tròn (C): (x + 1)2 + (y - 2)2 = 9 và điểm M(2;-1).
a) Chứng tỏ rằng qua M ta vẽ được hai tiếp tuyến Δ1 và Δ2 với (C), hãy viết phương trình của Δ1 và Δ2.
b) Gọi M1 và M2 lần lượt là hai tiếp điểm của Δ1 và Δ2 với (C) , hãy viết phương trình của đường thẳng d đi qua M1 và M2
Xem đáp án
a) (C) có tâm I(-1; 2) và có bán kính R = 3. Đường thẳng đi qua M(2; -1) và có hệ số góc k có phương trình:
y + 1 = k(x - 2) ⇔ kx - y - 2k - 1 = 0
Ta có: Δ tiếp xúc với (C) ⇔ d(I; Δ ) = R
Vậy ta được tiếp tuyến Δ1: y + 1 = 0
Xét đường thẳng Δ2 đo qua M(2;-1) và vuông góc với Ox, Δ2 có phương trình x - 2 = 0. Ta có:
d(I; Δ ) = |-1 - 2| = 3 = R
Suy ra Δ2 tiếp xúc với (C) .
Vậy qua điểm M ta vẽ được hai tiếp tuyến với (C), đó là:
Δ1: y + 1 = 0 và Δ2: x - 2 = 0
b) Δ1 tiếp xúc với (C) tại M1(-1; -1)
Δ2 tiếp xúc với (C) tại M2(2; 2)
Phương trình của đường thẳng d đi qua M1 và M2 là: x - y = 0.
Câu 12:
Viết phương trình tiếp tuyến của đường tròn (C) có phương trình x2 + y2 - 8x - 6y = 0 biết rằng tiếp tuyến đó đi qua gốc tọa độ O.
Xem đáp án
Đường tròn (C): x2 + y2 - 8x - 6y có tâm I(4;3) và bán kính R = 5.
Cách 1: xét đường thẳng Δ đi qua gốc tọa độ O và có hệ số góc k, Δ có phương trình y - kx = 0
Ta có: Δ tiếp xúc với (C) ⇔ d(I, Δ) = R
⇔ (3 - 4k)2 = 25(k2 + 1)
⇔ 9 - 24k + 16k2 = 25k2 + 25
⇔ 9k2 + 24k + 16 = 0
⇔ k = -4/3
Vậy ta được phương trình tiếp tuyến là: y + 4x/3 = 0 hay 4x + 3y = 0
Cách 2: Do tọa độ O(0;0) thỏa mãn phương trình của (C) nên điểm O nằm trên (C).
Tiếp tuyến với (C) tại O có vectơ pháp tuyến 
Suy ra Δ có phương trình: 4x + 3y = 0.
Câu 13:
Cho hai đường tròn (C1): x2 + y2 - 6x + 5 = 0 và (C2): x2 + y2 - 12x - 6y + 44 = 0
a) Tìm câm và bán kính của (C1) và (C2) .
b) Lập phương trình tiếp tuyến chung của (C1) và (C2).
Xem đáp án
a) (C1) có tâm có bán kính R1 = 2;
(C2) có tâm có bán kính R2 = 1.
b) Xét đường thẳng Δ có phương trình:
y = kx + m hay kx - y + m = 0. Ta có:
Δ tiếp xúc với (C1) và (C2) khi và chỉ khi
Từ (1) và (2) suy ra
|3k + 2| = 2|6k - 3 + m|
Trường hợp 1: 3k + m = 2(6k - 3 + m) ⇔ m = 6 - 9k (3)
Thay vào (2) ta được
⇔ 9 - 18k + 9k2 = k2 + 1
⇔ 8k2 - 18k + 8 = 0
⇔ 4k2 - 9k + 4 = 0
Thay giá trị của k vào (3) ta tính được
Vậy ta được hai tiếp tuyến
Δ1: y = k1x + 6 - 9k1
Δ2: y = k2x + 6 - 9k2
Trường hợp 2:
3k + m = -2(6k - 3 + m)
⇔ 3m = 6 - 15k
⇔ m = 2 - 5k (4)
Thay vào (2) ta được
⇔ (k - 1)2 = k2 + 1
⇔ k2 - 2k + 1 = k2 + 1
⇔ k = 0
Thay giá trị của k vào (4) ta được m = 2.
Vậy ta được tiếp tuyến Δ3: y = 2
Xét đường thẳng Δ4 vuông góc với Ox tại x0:
Δ4: x - x0 = 0
Δ4 tiếp xúc vơi (C1) và (C2) khi và chỉ khi
Vậy ta được tiếp tuyến: Δ4: x - 5 = 0
Tóm lại hai đường tròn (C1) và (C2) có bốn tiếp tuyến chung Δ1, Δ2, Δ3 và Δ4