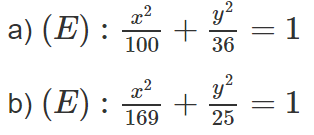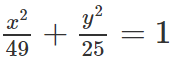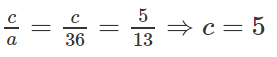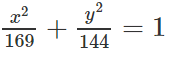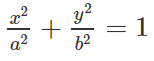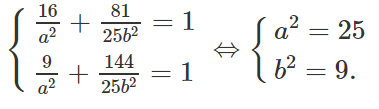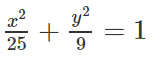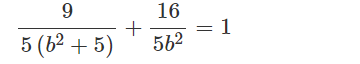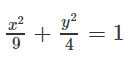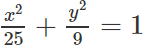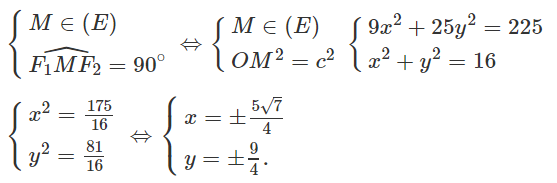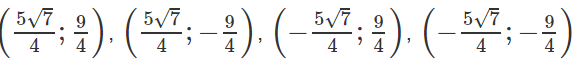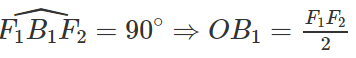Bài 3: Phương trình đường elip - SBT Hình học 10
-
2650 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Tìm tọa độ các tiêu điểm, các đỉnh, độ dài các trục của mỗi elip có phương trình sau:
a) 4x2 + 9y2 = 36;
b) x2 + 4y2 = 4.
Xem đáp án
a) 
- Hai tiêu điểm: F1(-√5; 0), F2(√5; 0)
- Bốn đỉnh: A1(-3; 0), A2(3; 0), B1(0; -2), B2(0; 2)
- Trục lớn: A1A2 = 6
- Trục nhỏ: B1B2 = 4
b) 
- Hai tiêu điểm: F1(-√3; 0), F2(√3; 0)
- Bốn đỉnh: A1(-2; 0), A2(3; 0), B1(0; -1), B2(0; 1)
- Trục lớn: A1A2 = 4
- Trục nhỏ: B1B2 = 2
Câu 3:
Cho đường tròn tâm C(F1; 2a) cố định và một điểm F2 cố định nằm trong (C1).
Xét đường tròn di động (C) có tâm M. Cho biết (C) luôn đi qua F2 và (C) luôn tiếp xúc với (C1). Hãy chứng tỏ M di động trên một elip.
Xem đáp án
C (M;R) đi qua F2 ⇒ MF2 = R(1)
C (M;R) tiếp xúc với C1(F1; 2a) ⇒ MF1 = 2a - R(2)
(1) + (2) cho MF1 + MF2 = 2a
Vậy M di động trên elip (E) có hai tiêu điểm là F1, F2 và trục lớn 2a.
Câu 4:
Trong mặt phẳng tọa độ Oxy cho M(x; y) di động có tọa độ thỏa mãn
trong đó t là tham số. Hãy chững tỏ M đi động trên một elip.
Xem đáp án
Điểm M di động trên elip (E) có phương trình:
Câu 5:
Viết phương trình chính tắc của elip trong các trường hợp sau:
a) Độ dài trục lớn bằng 26 và tỉ số c/a bằng 5/13;
b) Tiêu điểm F1(-6; 0) và tỉ số c/a bằng 2/3
Xem đáp án
a) Ta có: 2a = 26 ⇒ a = 13 và
Do đó: b2 = a2 - c2 = 169 - 25 = 144
Vậy phương trình chính tắc của elip là:
b) Elip có tiêu điểm F1(-6; 0) suy ra c = 6.
Do đó: b2 = a2 - c2 = 81 - 36 = 45
Vậy phương trình chính tắc của elip là:
Câu 6:
Viết phương trình chính tắc của elip (E) F1 và F2 biết:
a) (E) đi qua hai điểm M(4; 9/5) và N(3; 12/5);
b) (E) đi qua và tam giác MF1F2 vuông tại M.
Xem đáp án
a) Xét elip (E): 
(E) đi qua M(4; 9/5) và N(3; 12/5) nên thay tọa độ của M và N vào phương trình của (E) ta được:
Vậy phương trình của (E) là: 
b) Xét elip (E):
Thay vào (1) ta được :
⇒ 9b2 + 16(b2 + 5) = 5b2(b2 + 5)
⇒ b4 = 16
⇒ b2 = 4
Suy ra a2 = 9
Vậy phương trình chính tắc của (E) là: 
Câu 7:
Cho elip (E): 9x2 + 25y2 = 225
a) Tìm tọa độ hai điểm F1, F2 và các đỉnh của (E).
b) Tìm M ∈ (E) sao cho M nhìn F1, F2 dưới một góc vuông.
Xem đáp án
(E): 9x2 + 25y2 = 225 ⇔ 
a) Ta có: a2 = 25, b2 = 9
⇒ a = 5, b = 3
Ta có: c2 = a2 - b2 = 16
⇒ c = 4
Vậy (E) có hai tiêu điểm là : F1(-4; 0) và F2(4; 0) và có bốn đỉnh là A1(-5; 0), A2(5; 0), B1(0; -3), B2(0; 3)
b) Gọi M(x; y) là điểm cần tìm, ta có :
Vậy có bốn điểm M thỏa mãn điều kiện của đề bài là :
Câu 8:
Cho elip (E): (0 < b < a). Tính tỉ số: c/a trong các trường hợp sau:
a) Trục lớn bằng ba lần trục nhỏ ;
b) Đỉnh trên trục nhỏ nhìn hai tiểu điểm dưới một góc vuông ;
c) Khoảng cách giữa đỉnh trên trục nhỏ và đỉnh trên trục lớn bằng tiêu cự.
Xem đáp án
a) Ta có: a = 3b ⇒ a2 = 9b2
⇒ a2 = 9(a2 - c2)
⇒ 9c2 = 8a2
⇒ 3c = 2√2a
Vậy c/a = 2√2/3
b) 
⇒ b = c
⇒ b2 = c2
⇒ a2 - c2 = c2
⇒ a2 = 2c2
⇒ a = c√2
Vậy c/a = 1/√2
c) A1B1 = 2c ⇒ A1B21 = 4c2
⇒ a2 + b2 = 4c2
⇒ a2 + a2 - c2 = 4c2
⇒ 2a2 = 5c2
⇒ √2a = √5c
Vậy 
Câu 9:
Cho elip (E): 4x2 + 9y2 = 36 và điểm M(1; 1). Viết phương trình đường thẳng d đi qua M và cắt (E) tại hai điểm A và B sao cho M là trung điểm của AB.
Xem đáp án
(E): 4x2 + 9y2 = 36
Xét đường thẳng d đi qua điểm M(1;1) và có hệ số góc k. Ta có phương trình của
d: y - 1 = k(x - 1) hay y = k(x - 1) + 1 (2)
Thay (2) vào (1) ta được
4x + 9[k(x - 1) + 1]2 = 36
⇔ (9k2 + 4)x2 + 18k(1 - k) + 9(1 - k)2 - 36 = 0
Ta có : d cắt (E) tại hai điểm A, B thỏa mãn
MA = MB khi và chỉ khi phương trình (3) có hai nghiệm xA, xB sao cho:
Vậy phương trình của d là :
