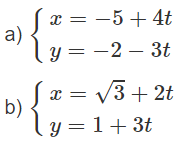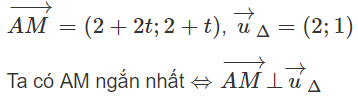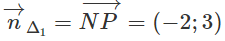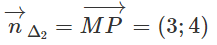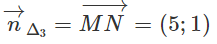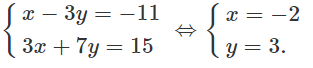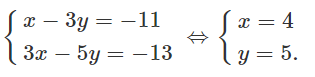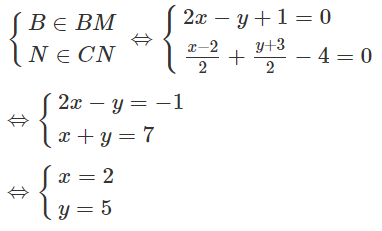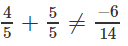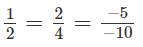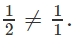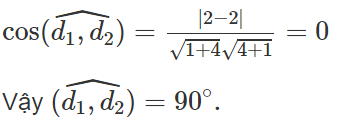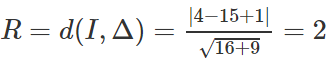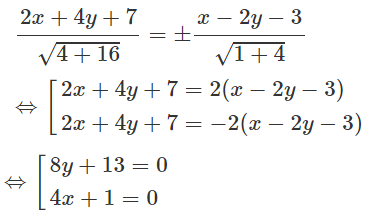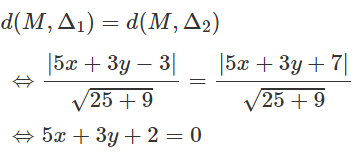Bài 1: Phương trình đường thẳng - SBT Hình học 10
-
2717 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Cho đường thẳng Δ có phương trình tham số
a) Tìm điểm M nằm trên Δ và cách điểm A(0; 1) một khoảng bằng 5.
b) Tìm tọa độ giao điểm của đường thẳng Δ với đường thẳng x + y + 1 = 0
c) Tìm M trên Δ sao cho AM ngắn nhất.
 Xem đáp án
Xem đáp án
a) M(2 + 2t; 3 + t) ∈ Δ
AM = 5 ⇔ (2 + 2t)2 + (2 + t)2 = 25
⇔ 5t2 + 12t - 17 = 0 ⇔ t = 1 hoặc t = -17/5
Vậy M có tọa độ là (4;4) hay (-24/5; -2/5)
b) M(2 + 2t; 3 + t) ∈ Δ
d: x + y + 1 = 0
M ∈ d ⇔ 2 + 2t + 3 + t + 1 = 0 ⇔ t = -2
Vậy M có tọa độ là (-2;1).
c) M(2 + 2t; 3 + t) ∈ Δ
⇔ 2(2 + 2t) + (2 + t) = 0 ⇔ t = -6/5
Vậy M có tọa độ là M(-2/5; 9/5)
Câu 3:
Lập Phương trình tổng quát của đường thẳng Δ trong mỗi trường hợp sau:
a) Δ đi qua điểm M(1;1) và có vectơ pháp tuyến vectơ n = (3; -2);
b) Δ đi qua điểm A(2;-1) và có hệ số góc k = -1/2;
c) Δ đi qua hai điểm A(2;0) và B(0;-3).
 Xem đáp án
Xem đáp án
a) 3x - 2y - 1 = 0
b) y + 1 = -(x - 2)/2 ⇔ x + 2y = 0
c) 3x - 2y - 6 = 0
Câu 4:
Lập phương trình ba đường trung trực của một tam giác có trung điểm các cạnh lần lượt là M(-1; 0), N(4; 1), P(2; 4).
 Xem đáp án
Xem đáp án
Gọi Δ1, Δ2, Δ3 lần lượt là các đường trung trực đi qua M, N, P.
Ta có:
Vậy Δ1 có phương trình: -2(x + 1) + 3y = 0 ⇔ 2x - 3y + 2 = 0
Ta có:
Vậy Δ2 có phương trình: 3(x - 4) + 4(y - 1) = 0 ⇔ 3x + 4y - 16 = 0
Ta có:
Vậy Δ2 có phương trình: 5(x - 2) + (y - 4) = 0 ⇔ 5x + y - 14 = 0
Câu 6:
Cho tam giác ABC, biết phương trình đường thẳng AB: x - 3y + 11 = 0, đường cao AH: 3x + 7y - 15 = 0, đường cao BH: 3x - 5y + 13 = 0. Tìm phương trình hai đường thẳng chứa hai cạnh còn lại của tam giác.
 Xem đáp án
Xem đáp án
Theo đề bài tọa độ điểm A luôn thỏa mãn hệ phương trình:
Vì AC ⊥ BH nên C có dạng: 5x + 3y + c = 0, ta có:
A ∈ AC ⇔ -10 + 9 + c = 0 ⇔ c = 1
Vậy phương trình đường thẳng chứa cạnh AC: 5x + 3y + 1 = 0.
Tọa độ của điểm B luôn thỏa mãn hệ phương trình:
Vì BC ⊥ AH nên BC có dạng: 7x - 3y + c = 0, ta có:
B ∈ BC ⇔ 28 - 15 + c = 0 ⇔ c = -13
Vậy phương trình đường thẳng chứa cạnh BC: 7x - 3y - 13 = 0.
Câu 7:
Cho tam giác ABC có A(-2; 3) và hai đường trung tuyến: 2x - y + 1 = 0 và x + y - 4 = 0. Hãy viết phương trình ba đường thẳng chứa ba cạnh của tam giác.
 Xem đáp án
Xem đáp án
Hai đường trung tuyến đã cho đều không phải là đường trung tuyến xuất phát từ A vì tọa độ A không thỏa mãn các phương trình của chúng. Đặt BM: 2x - y + 1 = 0 và CN: x + y - 4 = 0 là hai trung tuyến của tam giác ABC.
Đặt B(x;y), ta có 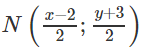
Vậy phương trình đường thẳng chứa cạnh AB là : 2x - 4y + 16 = 0
⇔ x - 2y + 8 = 0
Tương tự ta có phương trình đường thẳng chứa cạnh AC là : 2x + 5y - 11 = 0
Phương trình đường thẳng chứa cạnh BC là : 4x + y - 13 = 0
Câu 9:
Xét vị trí tương đối của các cặp đường thẳng sau đây:
a)
b) và d': 2x + 4y - 10 = 0
c) d: x + y - 2 = 0 và d': 2x + y - 3 = 0
 Xem đáp án
Xem đáp án
a) Đưa phương trình của d và d' về dạng tổng quát
d: 4x + 5y - 6 = 0
d': 4x + 5y + 14 = 0
Vậy d//d'
b) d:x + 2y - 5 = 0
d':2x + 4y - 10 = 0
Vậy d ≡ d'
c) d:x + y - 2 = 0
d':2x + y - 3 = 0
Vậy d cắt d'
Câu 12:
Lập phương trình các đường phân giác của các góc giữa hai đường thẳng
Δ1: 2x + 4y + 7 = 0 và Δ2: x - 2y - 3 = 0.
 Xem đáp án
Xem đáp án
Phương trình hai đường phân giác của các góc giữa Δ1 và Δ2 là:
Câu 14:
Viết phương trình đường thẳng đi qua điểm M(2; 5) và cách đều hai điểm A(-1; 2) và B(5; 4).
 Xem đáp án
Xem đáp án
Ta tìm thấy đường thẳng d1 đi qua M có vectơ chỉ phương là vectơ AB
và đường thẳng d2 đi qua M và trung điểm của AB.
d1: x - 3y + 13 = 0
d2: x - 2 = 0