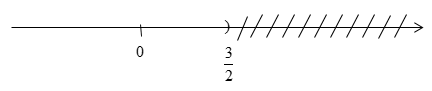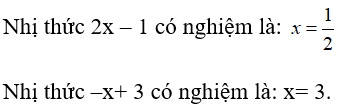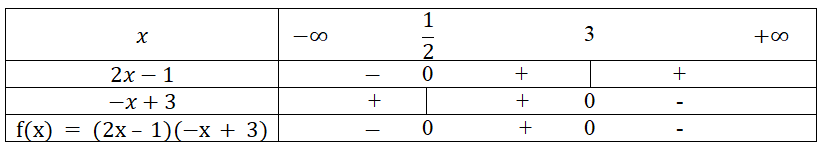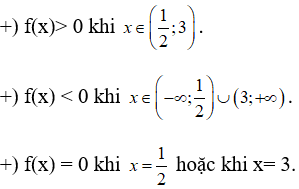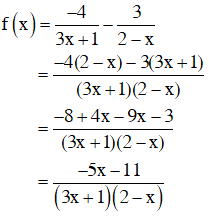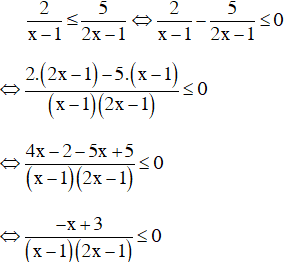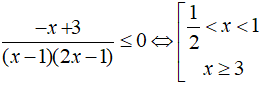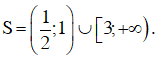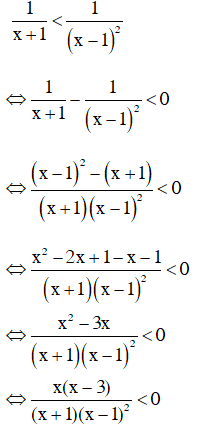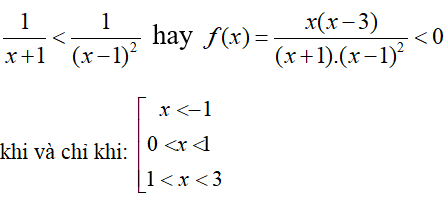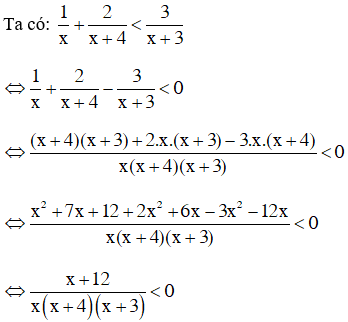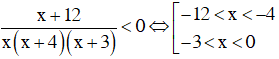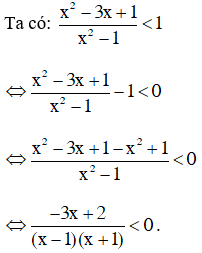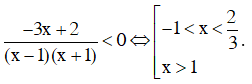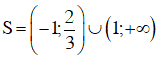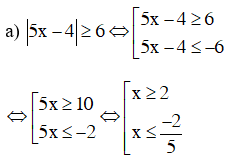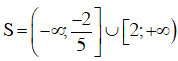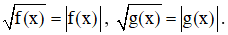Giải bài tập Toán lớp 10 Bài 3: Dấu của nhị thức bậc nhất
-
2002 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
a) Giải bất phương trình -2x + 3 > 0 và biểu diễn trên trục số tập nghiệm của nó.
b) Từ đó hãy chỉ ra các khoảng mà nếu x lấy giá trị trong đó thì nhị thức f(x) = -2x + 3 có giá trị
Trái dấu với hệ số của x;
Cùng dấu với hệ số của x.
Xem đáp án
a)-2x + 3 > 0 ⇔ -2x > -3 ⇔ x < 3/2
Biểu diễn tập nghiệm trên trục số:
b) Nhị thức f(x) = -2x + 3 có giá trị:
Trái dấu với hệ số của x khi x < 3/2
Cùng dấu với hệ số của x khi x > 3/2
Câu 2:
Xét dấu các nhị thức f(x) = 3x + 2, g(x) = -2x + 5.
Xem đáp án
Nhị thức 3x + 2 có nghiệm là: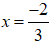 
. Bảng xét dấu của f(x)= 3x + 2:
Nhị thức – 2x + 5 có nghiệm là: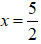 
. Bảng xét dấu của g(x) = -2x + 5
Câu 3:
Xét dấu biểu thức f(x) = (2x – 1)(-x + 3)
Xem đáp án
Các nghiệm này chia khoảng thành ba khoảng, trong mỗi
khoảng các nhị thức đã cho có dấu hoàn toàn xác định.
Từ bảng xét dấu ta thấy:
Câu 4:
Giải bất phương trình x3 – 4x < 0.
Xem đáp án
x3 – 4x < 0 ⇔ x(x2 - 4) < 0 ⇔ x(x - 2)(x + 2) < 0
Ta có bảng xét dấu
Từ bảng xét dấu ta có tập nghiệm của bất phương trình là:
S = (-∞;2) ∪ (0;2)
Câu 5:
Xét dấu các biểu thức:
Xem đáp án
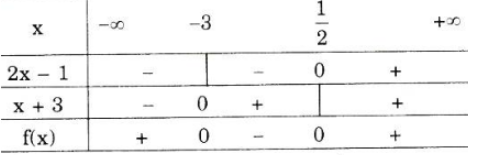
a) Nhị thức 2x – 1 có nghiệm là 1/2 ; nhị thức x + 3 có nghiệm là –3.
Ta có bảng xét dấu
Kết luận :
+ f(x) > 0 khi x < –3 hoặc x > 1/2
+ f(x) < 0 khi –3 < x < 1/2
+ f(x) = 0 khi x = –3 hoặc x = 1/2.
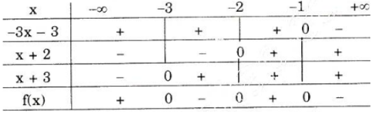
b) Nhị thức –3x – 3 có nghiệm là –1; nhị thức x + 2
có nghiệm là –2 ; nhị thức x + 3 có nghiệm là –3.
Ta có bảng xét dấu :
Kết luận :
+ f(x) < 0 khi –3 < x < –2 hoặc x > –1
+ f(x) > 0 khi x < –3 hoặc –2 < x < –1.
+ f(x) = 0 khi x = –3 hoặc x = –2 hoặc x = –1.
c) Ta có:
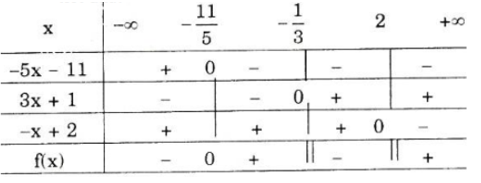
Nhị thức –5x – 11 có nghiệm là –11/5, nhị thức 3x +1
có nghiệm là –1/3, nhị thức 2 – x có nghiệm là 2.
Ta có bảng xét dấu:
Kết luận :
+ f(x) > 0 khi –11/5 < x < –1/3 hoặc x > 2.
+ f(x) < 0 khi x < –11/5 hoặc –1/3 < x < 2.
+ f(x) = 0 khi x = –11/5.
+ Khi x = –1/3 hoặc x = 2, f(x) không xác định.
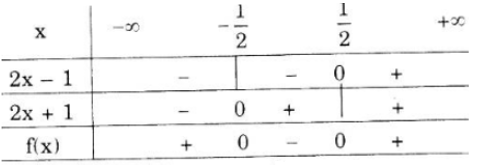
d) f(x) = 4x2 – 1 = (2x – 1)(2x + 1)
Nhị thức 2x – 1 có nghiệm x = 1/2, nhị thức 2x + 1 có
nghiệm x = –1/2.
Ta có bảng xét dấu:
Kết luận :
+ f(x) > 0 khi x < –1/2 hoặc x > 1/2.
+ f(x) < 0 khi –1/2 < x < 1/2
+ f(x) = 0 khi x = 1/2 hoặc x = –1/2.
Câu 6:
Giải các bất phương trình:
Xem đáp án
a) Điều kiện xác định x ≠ 1 và x ≠ 1/2.
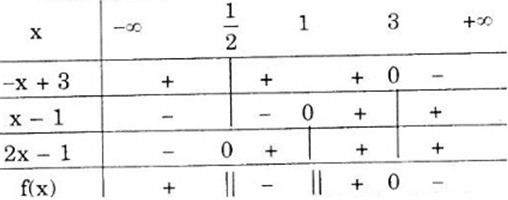
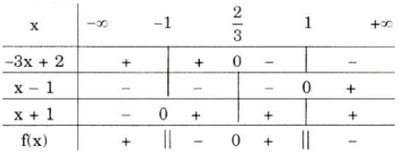
Các nhị thức –x + 3; x – 1; 2x – 1 có nghiệm lần lượt là 3; 1; 1/2.
Dựa vào bảng xét dấu thấy
Vậy tập nghiệm của bất phương trình là 
b) Điều kiện xác định x ≠ 1 và x ≠ –1.
Đặt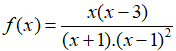 
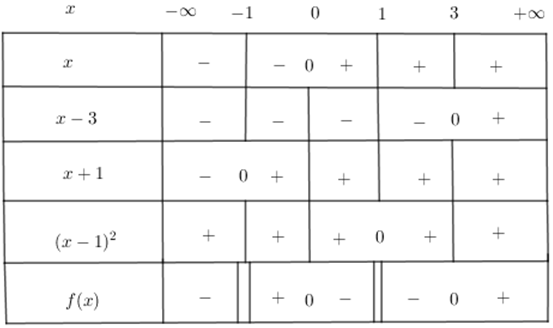
. Ta có bảng xét dấu sau:
Dựa vào bảng xét dấu ta thấy
Vậy bất phương trình có tập nghiệm S = (–∞; –1) ∪ (0; 1) ∪ (1; 3)
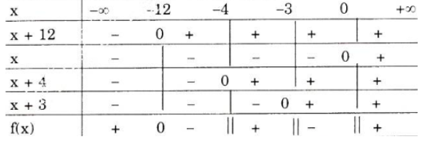
c) Điều kiện xác định x ≠ 0; x ≠ –3; x ≠ –4.
Đặt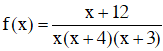 
. Ta có bảng xét dấu sau:
Dựa vào bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là S = (–12; –4) ∪ (–3; 0).
d) Điều kiện xác định x ≠ ±1.
Đặt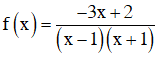 
. Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta thấy 
Vậy bất phương trình có tập nghiệm là 
Câu 7:
Giải các bất phương trình:
a) |5x - 4| ≥ 6
b)
Xem đáp án
Vậy bất phương trình có tập nghiệm
b) Điều kiện xác định x ≠ 1; x ≠ –2.
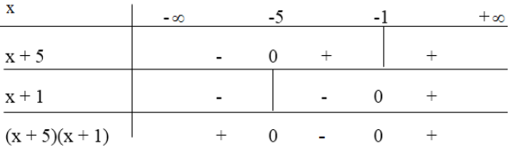
Ta có bảng xét dấu sau:
Dựa vào bảng xét dấu ta thấy (x + 1)(x + 5) > 0 khi x < -5 hoặc x > -1.
Kết hợp điều kiện x ≠ 1; x ≠ -2 vậy bất phương trình có tập nghiệm:
S = (–∞; -5) ∪ (-1; +∞)\{1}
Kiến thức áp dụng
+ Với a > 0 ta có:
|f(x)| ≤ a ⇔ –a ≤ f(x) ≤ a.
|f(x)| ≥ a ⇔ f(x) ≥ a hoặc f(x) ≤ –a
+ f2(x) ≤ g2(x) ⇔ |f(x)| ≤ |g(x)| vì 