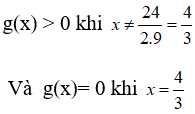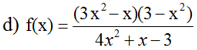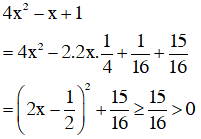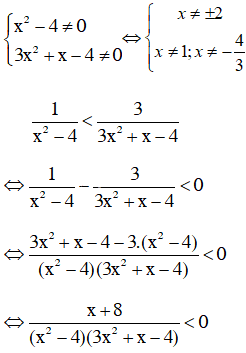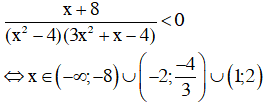Giải bài tập Toán lớp 10 Bài 5: Dấu của tam thức bậc hai
-
2240 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
1) Xét tam thức bậc hai f(x) = x2 – 5x + 4. Tính f(4), f(2), f(-1), f(0) và nhận xét về dấu của chúng.
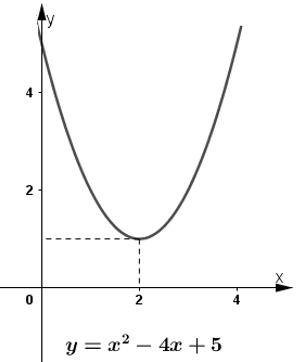
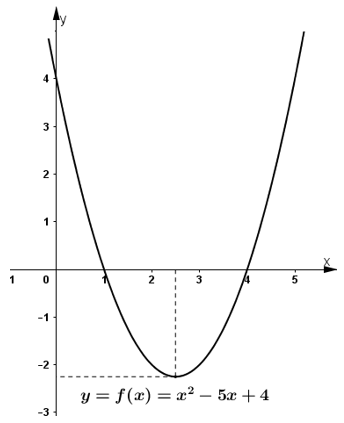
2) Quan sát đồ thị hàm số y = x2 – 5x + 4 (h.32a)) và chỉ ra các khoảng trên đó đồ thị ở phía trên, phía dưới trục hoành.
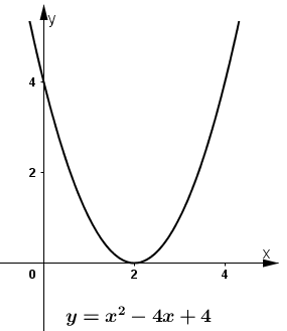
3) Quan sát các đồ thị trong hình 32 và rút ra mối liện hệ về dấu của giá trị f(x) = ax2 + bx + c ứng với x tùy theo dấu của biệt thức Δ = b2 – 4ac.
 Xem đáp án
Xem đáp án
a) f(x) = x2 – 5x +4
f(4)= 0; f(2) = -2 < 0; f(-1)= 10 > 0; f(0) = 4 > 0;
b) Với 1 < x < 4 thì đồ thị nằm phía dưới trục hoành.
Với x < 1 hoặc x > 4 thì đồ thị nằm phía trên trục hoành.
c) Hình 32a) có Δ > 0 ⇒ f(x) cùng dấu với a khi x nằm ngoài khoảng hai nghiệm của phương trình f(x) = 0; f(x) trái dấu với a khi x nằm trong khoảng hai nghiệm của phương trình f(x) = 0.
Hình 32b) có Δ = 0 ⇒ f(x) cùng dấu với a, trừ khi x = - b/2a.
Hình 32c) có Δ < 0 ⇒ f(x) cùng dấu với a.
Câu 2:
Xét dấu các tam thức
a) f(x) = 3x2 + 2x – 5;
b) g(x) = 9x2 – 24x + 16.
 Xem đáp án
Xem đáp án
a) f(x) = 3x2 + 2x – 5 có hai nghiệm phân biệt x = 1;
x = -5/3, hệ số a = 3 >0.
Ta có bảng xét dấu f(x) như sau:
b) Xét g(x) = 9x2 – 24x + 16 có Δ = (-24)2 - 4.9.16 = 0 và
hệ số a= 9> 0
Suy ra:
Câu 3:
Trong các khoảng nào
a) f(x) = -2x2 + 3x + 5 trái dấu với hệ số của x2 ?
b) g(x) = -3x2 + 7x – 4 cùng dấu với hệ số của x2 ?
 Xem đáp án
Xem đáp án
a)Tam thức f(x) = -2x2 + 3x + 5 có hai nghiệm là – 1 và 5/2 ; hệ số a= - 2 < 0.
Do đó, với -1 < x < 5/2 thì f(x) trái dấu với hệ số của x2
b)Tam thức g(x) = -3x2 + 7x – 4 có hai nghiệm là 1 và 4/3 , hệ số a= - 3 < 0
Do đó, với x < 1 hoặc x > 4/3 thì g(x) cùng dấu với hệ số của x2
Câu 4:
Xét dấu các tam thức bậc hai:
a) 5x2 - 3x + 1 ; b) -2x2 + 3x + 5
c) x2 + 12x + 36 ; d) (2x - 3)(x + 5)
 Xem đáp án
Xem đáp án
a) Tam thức f(x) = 5x2 – 3x + 1 có Δ = 9 – 20 = –11 < 0
nên f(x) cùng dấu với hệ số a.
Mà a = 5 > 0
Do đó f(x) > 0 với ∀ x ∈ R.
b) Tam thức f(x) = –2x2 + 3x + 5 có Δ = 9 + 40 = 49 > 0.
Tam thức có hai nghiệm phân biệt x1 = –1; x2 = 5/2, hệ số a = –2 < 0
Ta có bảng xét dấu:
Vậy f(x) > 0 khi x ∈ (–1; 5/2)
f(x) = 0 khi x = –1 ; x = 5/2
f(x) < 0 khi x ∈ (–∞; –1) ∪ (5/2; +∞)
c) Tam thức f(x) = x2 + 12x + 36 có một nghiệm là
x = –6, hệ số a = 1 > 0.
Ta có bảng xét dấu:
Vậy f(x) > 0 với ∀ x ≠ –6
f(x) = 0 khi x = –6
d) f(x) = (2x – 3)(x + 5) = 2x2 + 7x – 15
Tam thức f(x) = 2x2 + 7x – 15 có hai nghiệm phân biệt
x1 = 3/2; x2 = –5, hệ số a = 2 > 0.
Ta có bảng xét dấu:
Vậy f(x) > 0 khi x ∈ (–∞; –5) ∪ (3/2; +∞)
f(x) = 0 khi x = –5 ; x = 3/2
f(x) < 0 khi x ∈ (–5; 3/2)
Kiến thức áp dụng
Tam thức f(x) = ax2 + bx + c có Δ = b2 – 4ac:
+ Nếu Δ < 0, f(x) cùng dấu với a với ∀ x ∈ R
+ Nếu Δ = 0, f(x) cùng dấu với a với ∀ x ≠ –b/2a.
+ Nếu Δ > 0, f(x) cùng dấu với a nếu x < x1 hoặc x > x2;
f(x) trái dấu với a nếu x1 < x < x2; trong đó x1; x2 là hai nghiệm của f(x) và x1 < x2.
Câu 5:
Lập bảng xét dấu các biểu thức sau:
 Xem đáp án
Xem đáp án
a) f(x) = (3x2 – 10x + 3)(4x – 5)
+ Tam thức 3x2 – 10x + 3 có hai nghiệm x = 1/3 và
x = 3, hệ số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc
x > 3 và mang dấu – nếu 1/3 < x < 3.
+ Nhị thức 4x – 5 có nghiệm x = 5/4.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 khi x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)
f(x) = 0 khi x ∈ {1/3; 5/4; 3}
f(x) < 0 khi x ∈ (–∞; 1/3) ∪ (5/4; 3)
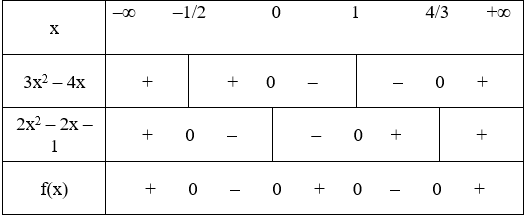
b) f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số
a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang
dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số
a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang
dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
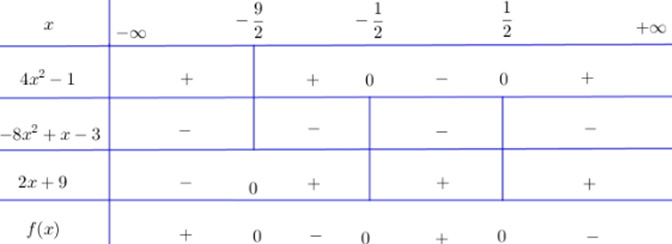
c) f(x) = (4x2 – 1)(–8x2 + x – 3)(2x + 9)
+ Tam thức 4x2 – 1 có hai nghiệm x = –1/2 và x = 1/2, hệ số
a = 4 > 0
Do đó 4x2 – 1 mang dấu + nếu x < –1/2 hoặc x > 1/2 và mang
dấu – nếu –1/2 < x < 1/2
+ Tam thức –8x2 + x – 3 có Δ = –95 < 0, hệ số a = –8 < 0 nên
luôn mang dấu –.
+ Nhị thức 2x + 9 có nghiệm x = –9/2.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 khi x ∈ (–∞; –9/2) ∪ (–1/2; 1/2)
f(x) = 0 khi x ∈ {–9/2; –1/2; 1/2}
f(x) < 0 khi x ∈ (–9/2; –1/2) ∪ (1/2; +∞)
+ Tam thức 3x2 – x có hai nghiệm x = 0 và x = 1/3, hệ số a = 3 > 0.
Do đó 3x2 – x mang dấu + khi x < 0 hoặc x > 1/3 và mang dấu –
khi 0 < x < 1/3.
+ Tam thức 3 – x2 có hai nghiệm x = √3 và x = –√3, hệ số a = –1 < 0
Do đó 3 – x2 mang dấu – khi x < –√3 hoặc x > √3 và mang dấu +
khi –√3 < x < √3.
+ Tam thức 4x2 + x – 3 có hai nghiệm x = –1 và x = 3/4, hệ số a = 4 > 0.
Do đó 4x2 + x – 3 mang dấu + khi x < –1 hoặc x > 3/4 và mang dấu –
khi –1 < x < 3/4.
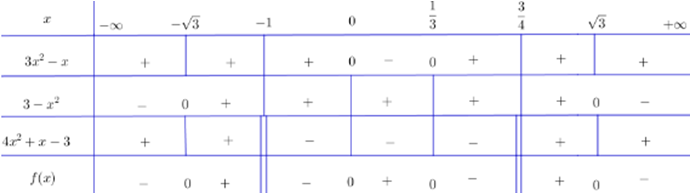
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 ⇔ x ∈ (–√3; –1) ∪ (0; 1/3) ∪ (3/4; √3)
f(x) = 0 ⇔ x ∈ {±√3; 0; 1/3}
f(x) < 0 ⇔ x ∈ (–∞; –√3) ∪ (–1; 0) ∪ (1/3; 3/4) ∪ (√3; +∞)
f(x) không xác định khi x = -1 và x = 3/4.
Kiến thức áp dụng
Tam thức f(x) = ax2 + bx + c có Δ = b2 – 4ac:
+ Nếu Δ < 0, f(x) cùng dấu với a với ∀ x ∈ R
+ Nếu Δ = 0, f(x) cùng dấu với a với ∀ x ≠ –b/2a.
+ Nếu Δ > 0, f(x) cùng dấu với a nếu x < x1 hoặc x > x2;
f(x) trái dấu với a nếu x1 < x < x2; trong đó x1; x2 là hai nghiệm của f(x) và x1 < x2.
Câu 6:
Giải các bất phương trình sau
a) 4x2 - x + 1 < 0
b) -3x2 + x + 4 ≥ 0
c)
d) x2 - x - 6 ≤ 0
 Xem đáp án
Xem đáp án
a) 4x2 - x + 1 < 0
Cách 1:
Xét tam thức f(x) = 4x2 - x + 1 có Δ = -15 < 0; a = 4 > 0
nên f(x) > 0 ∀x ∈ R
Vậy bất phương trình đã cho vô nghiệm.
Cách 2:
với ∀x ∈ R.
Vậy bất phương trình 4x2 – x + 1 < 0 vô nghiệm.
b) -3x2 + x + 4 ≥ 0
Xét tam thức f(x) = -3x2 + x + 4 có hai nghiệm x = -1 và
x = 4/3, hệ số a = -3 < 0.
Do đó f(x) ≥ 0 khi -1 ≤ x ≤ 4/3.
Vậy tập nghiệm của bất phương trình là: T = [-1; 4/3]
c) Điều kiện xác định
+ Nhị thức x + 8 có nghiệm x = -8
+ Tam thức x2 – 4 có hai nghiệm x = 2 và x = -2,
hệ số a = 1 > 0
Do đó x2 – 4 mang dấu + khi x < -2 hoặc x > 2 và mang
dấu – khi -2 < x < 2.
+ Tam thức 3x2 + x – 4 có hai nghiệm x = 1 và x = -4/3,
hệ số a = 3 > 0.
Do đó 3x2 + x – 4 mang dấu + khi x < -4/3 hoặc x > 1
mang dấu – khi -4/3 < x < 1.
Ta có bảng biến thiên
Dựa vào BBT ta thấy
Vậy tập nghiệm của bất phương trình là: T = (-∞; -8) ∪ (-2; -4/3) ∪ (1; 2)
d) x2 - x - 6 ≤ 0
Xét tam thức f(x) = x2 - x - 6 có hai nghiệm x = -2 và x = 3, hệ số a = 1 > 0
Do đó f(x) ≤ 0 khi -2 ≤ x ≤ 3.
Vậy tập nghiệm của bất phương trình là: T = [-2; 3]
Kiến thức áp dụng
Tam thức f(x) = ax2 + bx + c có Δ = b2 – 4ac:
+ Nếu Δ < 0, f(x) cùng dấu với a với ∀ x ∈ R
+ Nếu Δ = 0, f(x) cùng dấu với a với ∀ x ≠ –b/2a.
+ Nếu Δ > 0, f(x) cùng dấu với a nếu x < x1 hoặc x > x2;
f(x) trái dấu với a nếu x1 < x < x2; trong đó x1; x2 là hai nghiệm của f(x) và x1 < x2.
Câu 7:
Tìm các giá trị của tham số m để các phương trình sau vô nghiệm
a) (m - 2)x2 + 2(2m - 3)x + 5m - 6 = 0
b) (3 - m)x2 - 2(m + 3)x + m + 2 = 0
 Xem đáp án
Xem đáp án
a) (m - 2)x2 + 2(2m - 3)x + 5m - 6 = 0 (1)
- Nếu m - 2 = 0 ⇔ m = 2, khi đó phương trình (1) trở thành:
2x + 4 = 0 ⇔ x = -2 hay phương trình (1) có một nghiệm
Do đó m = 2 không phải là giá trị cần tìm.
- Nếu m - 2 ≠ 0 ⇔ m ≠ 2 ta có:
Δ' = (2m - 3)2 - (m - 2)(5m - 6)
= 4m2 - 12m + 9 - 5m2 + 6m + 10m - 12
= -m2 + 4m - 3 = (-m + 3)(m - 1)
(1) vô nghiệm ⇔ Δ' < 0 ⇔ (-m + 3)(m - 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)
Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.
b) (3 - m)x2 - 2(m + 3)x + m + 2 = 0 (2)
- Nếu 3 - m = 0 ⇔ m = 3 khi đó (2) trở thành -12x + 5 = 0 ⇔ x = 5/12
Do đó m = 3 không phải là giá trị cần tìm.
- Nếu 3 - m ≠ 0 ⇔ m ≠ 3 ta có:
Δ' = (m + 3)2 - (3 - m)(m + 2)
= m2 + 6m + 9 - 3m - 6 + m2 + 2m
= 2m2 + 5m + 3 = (m + 1)(2m + 3)
(2) vô nghiệm ⇔Δ' < 0⇔ (m + 1)(2m + 3) < 0 ⇔ m ∈ (-3/2; -1)
Vậy với m ∈ (-3/2; -1) thì phương trình vô nghiệm.
Kiến thức áp dụng
+ Phương trình dạng ax + b = 0 vô nghiệm khi a = 0 và b ≠ 0.
+ Phương trình bậc hai dạng ax2 + bx + c = 0 vô nghiệm khi Δ = b2 – 4ac < 0 hoặc Δ’ = (b/2)2 – ac < 0.