Đáp án cần chọn là: C

Hàm số xác định khi x – m ≠ 0 ⇔ x ≠ m.

⇒ Tập xác định của hàm số là D = R∖{m}.

Hàm số xác định trên (−1; 0) khi và chỉ khi m ∉ (−1; 0) ⇔  $\left[\begin{array}{c}m\ge 0\\ m\le -1\end{array}\right.$

Đáp án cần chọn là: A

Ta có:

$f\left(x_1\right)-f\left(x_2\right)=(x_1+\frac{1}{x_1})-(x_2+\frac{1}{x_2})$

$=(x_1-x_2)+(\frac{1}{x_1}-\frac{1}{x_2})=(x_1-x_2)(1-\frac{1}{x_1{x}_2})$

Với mọi $x_1,x_2\in \left(1;+\infty \right)$ và  $x_1<x_2$

Ta có  $\left\{\begin{array}{c}{x}_1>1\\ x_2>1\end{array}\Rightarrow x_1.x_1>1\Rightarrow \frac{1}{x_1.x_1}\right.<1$

Suy ra $\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=1-\frac{1}{x_1.x_2}>0\Rightarrow f\left(x\right)$ đồng biến trên  $\left(1,+\infty \right)$

Đáp án cần chọn là: C

Tập xác định D = R.

Hàm số đã cho đồng biến trên R ⇔ m + 1 > 0 ⇔ m > −1.

Mà m ∈ Z và m ∈ [−3; 3] nên m ∈ {0; 1; 2; 3}.

Đáp án cần chọn là: A

Phương trình (C_m′): y = m(x + 1)² − 2(m − 1) (x + 1) + 1

Phương trình hoành độ giao điểm:

mx² − 2(m − 1)x + 1 = m(x + 1)² − 2(m −1 )(x + 1) + 1

 ⇔ 2mx + m − 2(m − 1) = 0 ⇔ 2mx – m + 2 = 0 ⇔  $x=\frac{m-2}{2m}$

Giao điểm có hoành độ x = $\frac{1}{4}$  nên $\frac{m-2}{2m}=\frac{1}{4}$  ⇔ m = 4

Đối chiếu các đáp án ta thấy 1 < m < 5.

Đáp án cần chọn là: A

Tập xác định D = R nên ∀x ∈ D ⇒ −x ∈ D.

Ta có f(−x) = (−x)³ + (m² − 1)(−x)² + 2(−x) + m – 1 = −x³ + (m² − 1)x² − 2x + m− 1.

Để hàm số đã cho là hàm số lẻ khi f(−x) = −f(x), với mọi x ∈ D

⇔ −x³ + (m² − 1)x² − 2x + m – 1 = −[x³ + (m² − 1)x² + 2x + m − 1],

 với mọi x ∈ D

⇔ 2(m² − 1)x² + 2(m − 1) = 0, với mọi x ∈ D

⇔ $\left\{\begin{array}{c}{m}^2-1=0\\ m-1=0\end{array}\right.$⇔ m = 1 ∈ ($\frac{1}{2}$; 3).

Đáp án cần chọn là: C

Với mọi $x_1\ne x_2,$ ta có

$\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\frac{\left[-x_1^2+(m-1)x_1+2\right]-\left[-x_2^2+(m-1)x_2+2\right]}{x_1-x_2}$

$=-(x_1+x_2)+m-1$

Để hàm số nghịch biến trên (1; 2) ⇔ − (x₁ + x₂) + m – 1 < 0, với mọi x₁, x₂ ∈ (1; 2)

⇔ m < (x₁ + x₂) + 1, với mọi x₁, x₂ ∈ (1; 2)

⇔ m < (1 + 1) + 1 = 3

Đáp án cần chọn là: C

Hàm số $y=\frac{x+1}{x-2m+1}$ xác định trên $\left[0;1\right)$ nếu:

 $\begin{array}{l}x-2m+1\ne 0,\forall x\in \left[0;1\right)\iff x\ne 2m-1,\forall x\in \left[0;1\right)\iff 2m-1\notin \left[0;1\right)\\ \iff \left[\begin{array}{c}2m-1<0\\ 2m-1\ge 1\end{array}\right.\iff \left[\begin{array}{c}m<\frac{1}{2}\\ m\ge 1\end{array}\right.\end{array}$

Đáp án cần chọn là: A

Hàm số xác định khi  $\begin{array}{l}\left\{\begin{array}{c}x-m+1\ge 0\\ -x+2m>0\end{array}\right.\iff \left\{\begin{array}{c}x\ge m-1\\ x<2m\end{array}\right.\\ \end{array}$

$\Rightarrow$ Tập xác định của hàm số $D=\left[m-1;2m\right)$ với điều kiện $m-1\le 2m\iff m>-1$ 

Hàm số đã cho xác định trên (-1; 3) khi và chỉ khi  $\left(-1;3\right)\subset \left[m-1;2m\right)$

$\iff m-1\le -1<3\le 2m\iff \left\{\begin{array}{c}m\le 0\\ m\ge \frac{3}{2}\end{array}\right.\iff m\in \varnothing$

$m\le \frac{m+1}{2}\iff m\le 1$

Đáp án cần chọn là: D

Hàm số xác định khi  $\left\{\begin{array}{c}x-m\ge 0\\ 2x-m-1\ge 0\end{array}\right.\iff \left\{\begin{array}{c}x\ge m\\ x\ge \frac{m+1}{2}\end{array}\right.(*)$

TH1: Nếu $m\ge \frac{m+1}{2}\iff m\ge 1$ thì  (*) $\iff x\ge m$

⇒ Tập xác định của hàm số là D = [m; +∞).

Khi đó, hàm số xác định trên (0; +∞) khi và chỉ khi (0; +∞) ⊂ [m; +∞) ⇔ m ≤ 0

⇒ Không thỏa mãn điều kiện m ≥ 1.

TH2: Nếu $m\le \frac{m+1}{2}\iff m\le 1$ thì (*) $\iff x\ge \frac{m+1}{2}$

⇒ Tập xác định của hàm số là  $D=\left[\frac{m+1}{2};+\infty \right)$

Khi đó, hàm số xác định trên (0; +∞) khi và chỉ khi 

(0; +∞)⊂  $\left[\frac{m+1}{2};+\infty \right)\iff \frac{m+1}{2}\le 0\iff m\le -1$

⇒ Thỏa mãn điều kiện m ≤ 1.  Vậy m ≤ −1 thỏa yêu cầu bài toán.

Đáp án cần chọn là: A

Lấy $-1<x_1<x_2<0$ thì $x_2-x_1>0$ ta có:

$T_1=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=\frac{x_2-x_1}{x_2-x_1}=1>0,\forall x_1,x_2\in \left(-1;0\right)$ nên đáp án A đúng

$T_2=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=\frac{\frac{1}{x_2}-\frac{1}{x_1}}{x_2-x_1}=\frac{x_1-x_2}{x_1{x}_2{(x_2-x_1)}_{}}=-\frac{1}{x_1{x}_2}<0,\forall x_1,x_2\in \left(-1;0\right)$ nên B sai.

$T_3=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=\frac{\left|x_2\right|-\left|x_1\right|}{x_2-x_1}=\frac{-x_2+x_1}{{(x_2-x_1)}_{}}=-1<0,\forall x_1,x_2\in \left(-1;0\right)$ nên C sai

 $T_4=\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}=\frac{{x^2}_2-x_1^2}{x_2-x_1}=x_2+x_1<0,\forall x_1,x_2\in \left(-1;0\right)$ nên D sai

Đáp án cần chọn là: A

Ta có:$f\left(x_1\right)-f\left(x_2\right)=(x_1^2-4x_1+5)-(x_2^2-4x_2+5)$

$=(x_1^2-x_2^2)-4(x_1-x_2)=(x_1-x_2)(x_1+x_2-4)$

Với mọi $x_1,x_2\in \left(-\infty ;2\right)$ và x₁ < x₂.

Ta có $\left\{\begin{array}{c}{x}_1<2\\ x_2<2\end{array}\right.\Rightarrow x_1+x_2<4$

Suy ra  $\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\frac{(x_1-x_2)(x_1+x_2-4)}{x_1-x_2}=x_1+x_2-4<0$

Vậy hàm số nghịch biến trên  $\left(-\infty ;2\right)$

Với mọi $x_1,x_2\in \left(2,+\infty \right)$ và $x_1<x_2$. Ta có  $\left\{\begin{array}{c}{x}_1>2\\ x_2>2\end{array}\right.\Rightarrow x_1+x_2>4$

Suy ra $\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\frac{(x_1-x_2)(x_1+x_2-4)}{x_1-x_2}=x_1+x_2-4>0$

Vậy hàm số đồng biến trên  $\left(2;+\infty \right)$

Đáp án cần chọn là: B

TXĐ: $D=\left[\frac{7}{2};+\infty \right)$ nên ta loại đáp án C và D.

Xét  $f\left(x_1\right)-f\left(x_2\right)=\sqrt{2x_1-7}-\sqrt{2x_2-7}=\frac{2(x_1-x_2)}{\sqrt{2x_1-7}+\sqrt{2x_2-7}}$

Với mọi $x_1,x_2\in (\frac{7}{2};+\infty )$ và $x_1<x_2$, ta có:

$\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\frac{2}{\sqrt{2x_1-7}+\sqrt{2x_2-7}}>0$

Vậy hàm số đồng biến trên $(\frac{7}{2};+\infty )$

Đáp án cần chọn là: C

Xét f(x) = |x+2| − |x−2| có TXĐ: D = R nên ∀x ∈ D ⇒ −x ∈ D.

Ta có f(−x) = |(−x) + 2| − |(−x) − 2| = |−x + 2| − |−x − 2|

= |x − 2| − |x + 2| = − (|x + 2| − |x − 2|) = −f(x) ⇒ f(x) là hàm số lẻ.

Xét f(x) = |2x + 1| + $\sqrt{4x^2-4x+1}$ = |2x + 1| + $\sqrt{{(2x-1)}^2}$ = |2x + 1| + |2x − 1| có

TXĐ: D = R nên ∀x ∈ D ⇒ −x ∈ D.

Ta có f(−x) = |2 (−x) + 1| + |2 (−x) − 1| =| −2x + 1| + |−2x − 1|

= |2x − 1| + |2x + 1| = |2x + 1| + |2x − 1| = f(x) ⇒ f(x) là hàm số chẵn.

Xét f(x) = x(|x| − 2) có TXĐ: D = R nên ∀x ∈ D ⇒ −x ∈ D.

Ta có f(−x) = (−x) (|−x| − 2) = −x (|x| − 2) = −f(x) ⇒ f(x) là hàm số lẻ.

Xét $f\left(x\right)=\frac{\left|x+2015\right|+\left|x-2015\right|}{\left|x+2015\right|-\left|x-2015\right|}$ có TXĐ: D = R∖{0} nên ∀x ∈ D ⇒ −x ∈ D

Ta có  $f(-x)=\frac{\left|-x+2015\right|+\left|-x-2015\right|}{\left|-x+2015\right|-\left|-x-2015\right|}=f\left(x\right)=\frac{\left|x-2015\right|+\left|x+2015\right|}{\left|x-2015\right|-\left|x+2015\right|}$

$=-\frac{\left|x+2015\right|+\left|x-2015\right|}{\left|x+2015\right|-\left|x-2015\right|}=-f\left(x\right)\Rightarrow f\left(x\right)$ là hàm số lẻ.

Vậy có tất cả 3 hàm số lẻ.

Đáp án cần chọn là:D

Hàm số xác định khi  $\left\{\begin{array}{c}x-m+2\ge 0\\ \sqrt{x-m+2}-1\ne 0\end{array}\right.\iff \left\{\begin{array}{c}x\ge m-2\\ x\ne m-1\end{array}\right.$

$\Rightarrow$Tập xác định của hàm số là $D=\left[m-2;+\infty \right)$\ $\left\{m-1\right\}$

Hàm số trên xác định trên (0; 1) khi và chỉ khi $\left(0;1\right)\subset \left[m-2;+\infty \right)$\ $\left\{m-1\right\}$

 $\iff \left[\begin{array}{c}m-2\le 0<1\le m-1\\ m-1\le 0\end{array}\right.\iff \left[\begin{array}{c}\left\{\begin{array}{c}m\le 2\\ m\ge 2\end{array}\right.\\ m\le 1\end{array}\right.\iff \left[\begin{array}{c}m=2\\ m\le 1\end{array}\right.$

Đáp án cần chọn là: A

Hàm số $y=\sqrt{\frac{x^3}{\left|x\right|-2}}$ xác định nếu  $\frac{x^3}{\left|x\right|-2}\ge 0$

Ta có  $\left|x\right|-2=0\iff \left[\begin{array}{c}x=2\\ x=-2\end{array};x^3\right.=0\iff x=0$

Xét dấu biểu thức $\frac{x^3}{\left|x\right|-2}$ ta có:

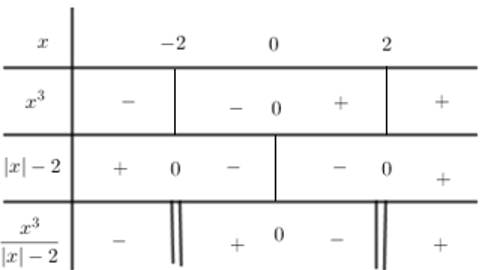
Khi đó tập xác định của hàm số là (−2; 0] ∪ (2; +∞).