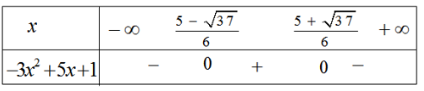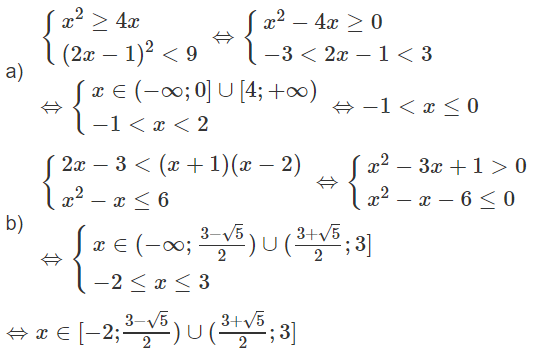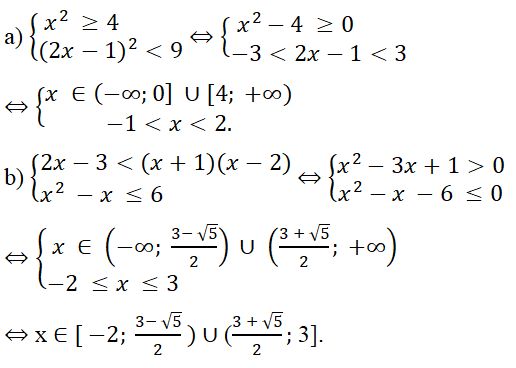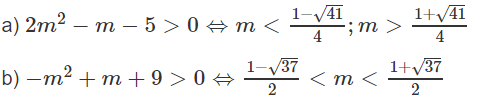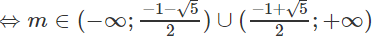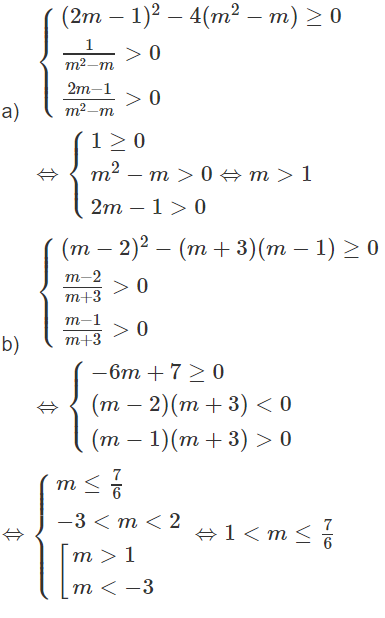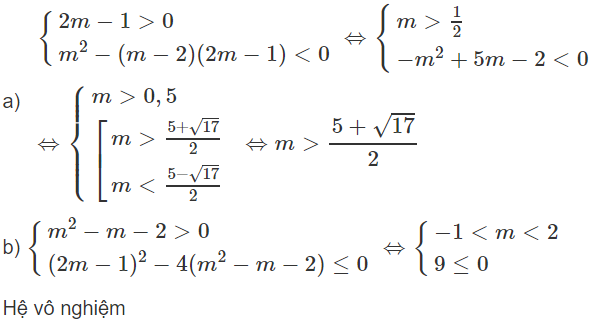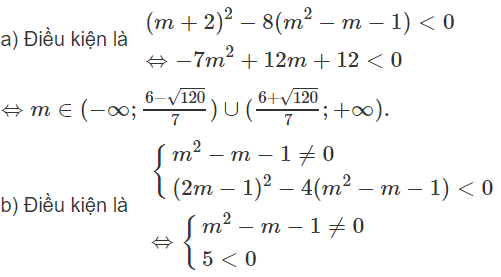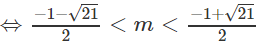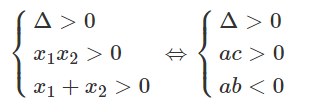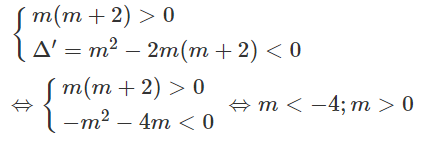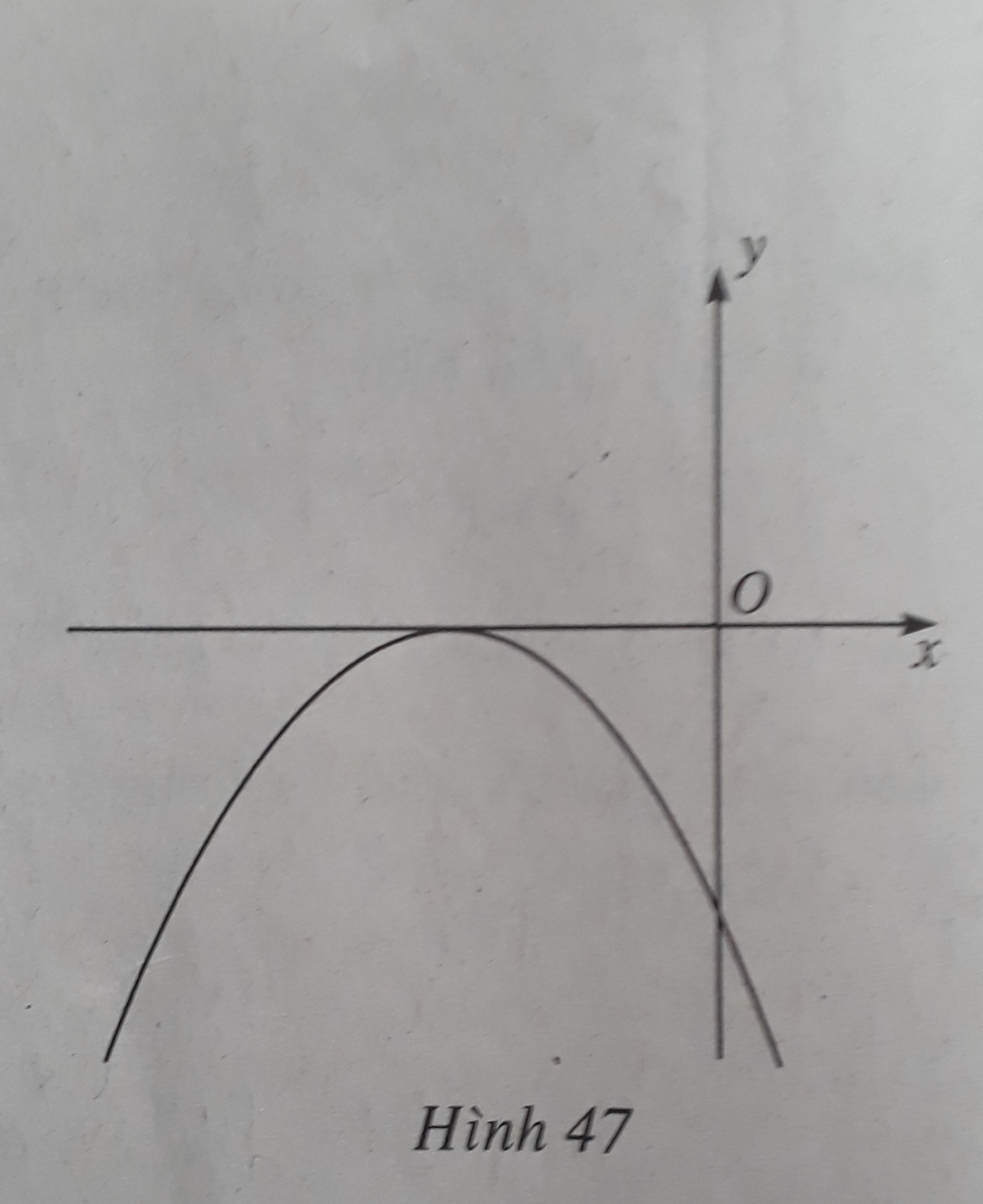25 câu hỏi trắc nghiệm thuộc Bài 5: Dấu của tam thức bậc hai - SBT Đại số 10

Câu 1:

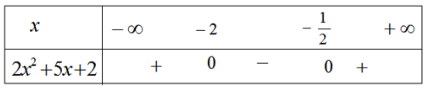
Xét dấu của tam thức bậc hai sau

a) $2 x^{2} + 5 x + 2$

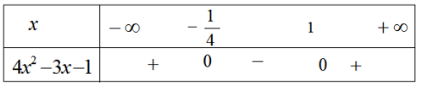
b) $4 x^{2} - 3 x - 1$

c) $- 3 x^{2} + 5 x + 1$

d) $3 x^{2} + x + 5$

Xem đáp án

a)

b)

c)

d) Tam thức 3x² + x + 5 có biệt thức Δ = -59 < 0 và hệ số a = 3 > 0

Vậy 3x² + x + 5 > 0, ∀x

Câu 2:

Giải các bất phương trình sau:

a) x² - 2x + 3 > 0;

b) x² + 9 > 6x.

Xem đáp án

a) x² - 2x + 3 > 0 ⇔ (x + 1)² + 2 > 0 (đúng với mọi x vì (x+1)² ≥ 0 ∀ x ⇒ (x+1)² + 2 ≥ 2 > 0)

b) x² + 9 > 6x ⇔ x² - 6x + 9 > 0 ⇔ (x - 3)² > 0 ⇔ x - 3 ≠ 0 ⇔ x ≠ 3

Câu 3:

Giải các bất phương trình sau:

a) 6x² - x - 2 ≥ 0;

b) (x² / 3) + 3x + 6 < 0.

Xem đáp án

a) 6x² - x - 2 ≥ 0 ⇔ x ≤ -1/2 hoặc x ≥ 2/3

b) (x² / 3) + 3x + 6 < 0 ⇔ x² + 9x + 18 < 0 ⇔ -6 < x < -3

Câu 4:

Giải các bất phương trình sau:

a) $\frac{x^{2} + 1}{x^{2} + 3 x - 10} < 0$

b) $\frac{10 - x}{5 + x^{2}} > \frac{1}{2}$

Xem đáp án

Câu 5:

Giải các bất phương trình sau:

a) $\frac{x + 1}{x - 1} + 2 > \frac{x - 1}{x}$

b) $\frac{1}{x + 1} + \frac{2}{x + 3} < \frac{3}{x + 2}$

Xem đáp án

Câu 6:

Giải các bất phương trình sau:

a) $\{\begin{cases} x^{2} \geq 0, 25 \\ x^{2} - x \leq 0 \end{cases}$

b) $\{\begin{cases} (x - 1) (2 x + 3) > 0 \\ (x - 4) (x + \frac{1}{4}) \leq 0 \end{cases}$

Xem đáp án

Câu 7:

Giải các bất phương trình sau:

a) $\{\begin{cases} x^{2} \geq 4 \\ {(2 x - 1)}^{2} \leq 9 \end{cases}$

b) $\{\begin{cases} 2 x - 3 \leq (x + 1) (x - 2) \\ x^{2} - x < 6 \end{cases}$

Xem đáp án

Câu 8:

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:

a) $2 m^{2} - m - 5 > 0$

b) $- m^{2} + m + 9 > 0$

Xem đáp án

Câu 9:

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:

a) (2m - 1)² - 4(m + 1)(m - 2) ≥ 0

b) m² - (2m - 1)(m + 1) < 0

Xem đáp án

a) (2m - 1)² - 4(m + 1)(m - 2) ≥ 0 ⇔ 9 ≥ 0. Bất phương trình có tập nghiệm là R.

b) m² - (2m - 1)(m + 1) < 0 ⇔ -m² - m + 1 < 0

Câu 10:

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:

a) $\{\begin{cases} {(2 m - 1)}^{2} - 4 (m^{2} - m) \geq 0 \\ \frac{1}{m^{2} - m} > 0 \\ \frac{2 m - 1}{m^{2} - m} > 0 \end{cases}$

b) $\{\begin{cases} {(m - 2)}^{2} - (m + 3) (m - 1) \geq 0 \\ \frac{m - 2}{m + 3} > 0 \\ \frac{m - 1}{m + 3} > 0 \end{cases}$

Xem đáp án

Câu 11:

Giải các bất phương trình, hệ bất phương trình (ẩn m) sau:

a) $\{\begin{cases} 2 m - 1 > 0 \\ m^{2} - (m - 2) (2 m - 1) < 0 \end{cases}$

b) $\{\begin{cases} m^{2} - m - 2 > 0 \\ {(2 m - 1)}^{2} - 4 (m^{2} - m - 2) \leq 0 \end{cases}$

Xem đáp án

Câu 12:

Tìm các giá trị của tham số m để các tam thức bậc hai sau có dấu không đổi (không phụ thuộc vào x).

a) f(x) = 2x² - (m + 2)x + m² - m + 1

b) f(x) = (m² + m + 1)x² - (2m - 1)x + 1

Xem đáp án

Để tam thức bậc hai f(x) = ax2 + bx + c dấu không đổi, điều kiện cần và đủ là Δ = b2 - 4ac < 0

Không có giá trị nào của m thỏa mãn điều kiện này.

Câu 13:

Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm phân biệt trái dấu

a) (m² - 1)x² + (m + 3)x + (m² + m) = 0

b) x² - (m³ + m - 2)x + m² + m - 5 = 0.

Xem đáp án

Phương trình bậc hai ax² + bx + c = 0 sẽ có hai nghiệm phân biệt trái dấu khi và chỉ khi ac < 0.

a) Nếu m = 1 hoặc m = -1 thì phương trỉnh đã cho có nghiệm duy nhất (loại).

(m² - 1)(m² + m) < 0 ⇔ (m + 1)²m(m - 1) < 0

⇔ 0 < m < 1

b) x² - (m³ + m - 2)x + m² + m - 5 = 0 có hai nghiệm phân biệt trái dấu khi và chỉ khi m² + m - 5 < 0

Câu 14:

Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm dương phân biệt

a) x² - 2x + m² + m + 3 = 0;

b) (m² + m + 3)x² + (4m² + m + 2)x + m = 0

Xem đáp án

Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm dương phân biệt, điều kiện cần và đủ là:

a) x² - 2x + m² + m + 3 = 0 có Δ' = -m² - m - 2 < 0, ∀m. Do đó không có giá trị nào của m thỏa mãn yêu cầu bài toán.

b) (m² + m + 3)x² + (4m² + m + 2)x + m = 0 có a = m² + m + 3 > 0, ∀m và có b = 4m² + m + 2 > 0, ∀m, nên ab > 0, ∀m. Vì vậy không có giá trị nào của m để phương trình đã cho có hai nghiệm dương phân biệt.

Câu 15:

Với giá trị nào của tham số m hệ phương trình có nghiệm thỏa mãn điều kiện x > 0, y < 0?

$\{\begin{cases} 2 x - (m^{2} + m + 1) y = - m^{2} - 9 \\ m^{4} + (2 m^{2} + 1) y = 1 \end{cases}$

Xem đáp án

Chú ý rằng m² + m + 1 > 0; -m² - 9 < 0, ∀m nên nếu x > 0, y < 0 thì phương trình thứ nhất có vế trái dương, vế phải âm. Do đó không có giá trị nào của m làm cho hệ đã cho có nghiệm thỏa mãn điều kiện x > 0, y < 0.

Câu 16:

Tìm các giá trị của tham số m để các bất phương trình sau nghiệm đúng với mọi x

5x² - x + m > 0

Xem đáp án

5x² - x + m > 0, ∀x

⇔ Δ = 1 - 20m < 0 Δ m > 1/20

Câu 17:

Tìm các giá trị của tham số m để các bất phương trình sau nghiệm đúng với mọi x

m(m + 2)x² + 2mx + 2 > 0

Xem đáp án

+ Nếu m = 0 thì bất phương trình nghiệm đúng với mọi x;

+ Nếu m = -2 thì bất phương tình trở thành – 4x + 2 > 0, không nghiệm đúng với mọi x.

+ Nếu m ≠ 0 và m ≠ -2 thì bất phương trình nghiệm đúng với mọi x khi và chỉ khi

Đáp số: m < -4; m ≥ 0

Câu 18:

Tìm m để bất phương trình sau vô nghiệm

5x² - x + m ≤ 0

Xem đáp án

Bất phương trình đã cho vô nghiệm khi và chỉ khi 5x² - x + m > 0 nghiệm đúng với mọi x.

⇔ 1 - 20m < 0 ⇔ m > 1/20

Đáp số: m > 1/20

Câu 19:

Tìm m để phương trình sau có hai nghiệm dương phân biệt

(m² + m + 1)x² + (2m - 3)x + m - 5 = 0

Xem đáp án

Phương trình đã cho có hai nghiệm dương x₁, x₂ phân biệt khi và chỉ khi

Vì m² + m + 1 > 0 nên bất phương trình (1) ⇔ m < 3/2 và bất phương trình (2) ⇔ m > 5

Do dó không có giá trị của m thỏa mãn yêu cầu bài toán.

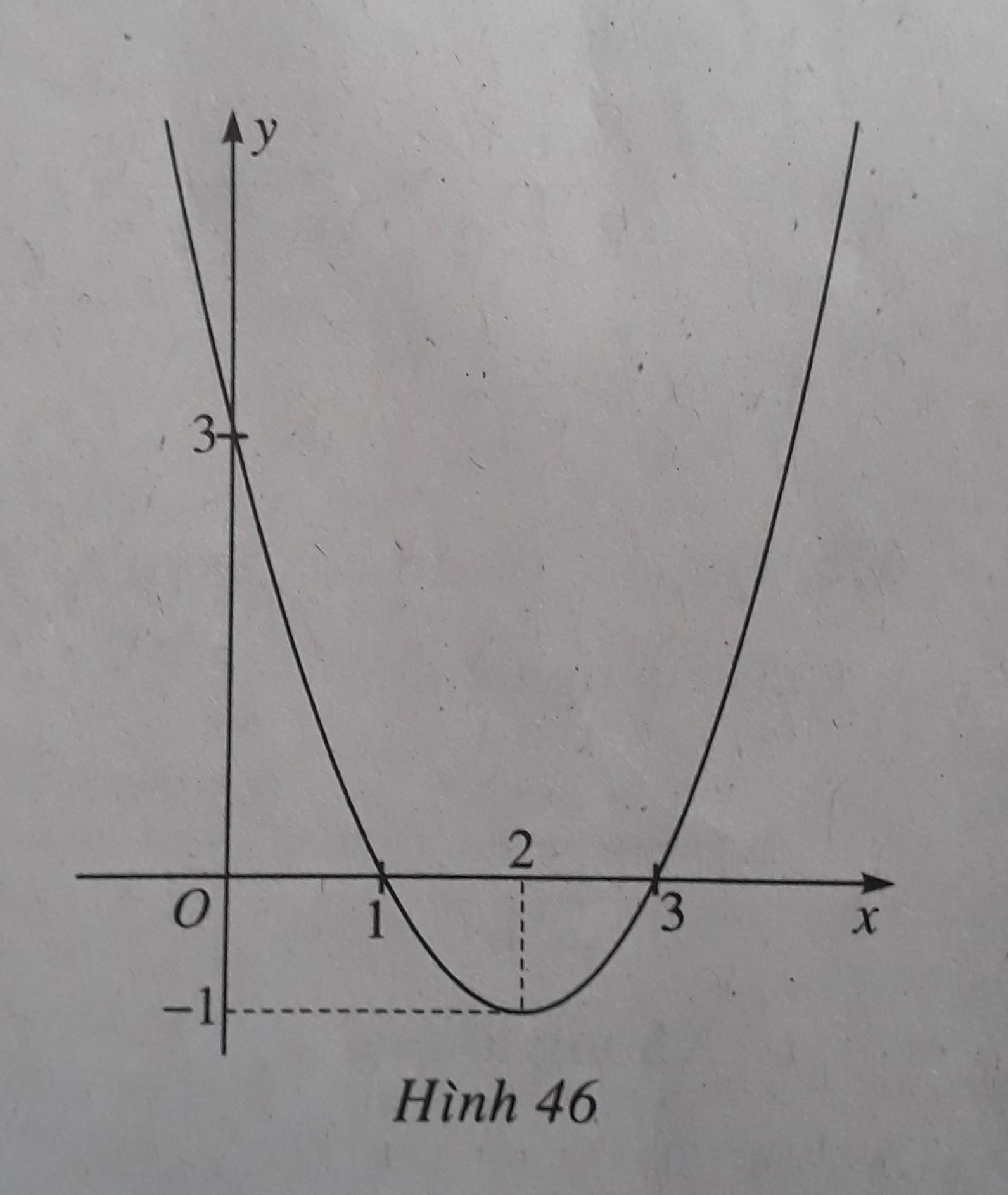
Câu 20:

Đồ thị hàm số y = f(x) = x² - 4x + 3 được cho trong hình 46. Từ hình vẽ nãy hãy chỉ ra tập nghiệm của bất phương trình x² - 4x + 3 > 0

A. x < 1

B. x ≥ 1

C. 1 < x < 3

D. (-∞; 1) ∪ (3; +∞)

Xem đáp án

Đáp án: D

Câu 21:

Đồ thị hàm số y = f(x) = ax² + bx + c được cho trong hình 47. Kí hiệu Δ = b² - 4ac là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?

A. a, b trái dấu

B. f(x) ≤ 0, ∀x

C. a < 0, c < 0

D. Δ = 0, a < 0

Xem đáp án

Đáp án: A

Câu 22:

Tập nghiệm của bất phương trình -3x² + x + 4 ≥ 0 là:

A. S = ∅

B. S = (-∞; -1] ∪ [4/3; +∞]

C. S = [-1; 4/3]

D. S = (-∞; +∞)

Xem đáp án

Đáp án: C

Câu 23:

Tìm tập xác định của hàm số

$y = \sqrt{\frac{x^{2} + x + 2}{x^{2} + 1}}$

A. x < -2; x ≤ -2;

B. x ≤ -2; x ≥ -1

C. x ≤ -2; x ≤ -2;

D. x ≤ -2; -1 < x < 1; x > 1

Xem đáp án

Đáp án: D

Câu 24:

Tìm các giá trị của tham số m để phương trình mx² + 2(2m - 1)x + m + 2 = 0 vô nghiệm

A. $\frac{3 - \sqrt{6}}{3} < m < \frac{3 + \sqrt{6}}{3}$

B. Không tồn tại m

C. m < 1/12

D. m ≠ 0; m < 1/12

Xem đáp án

Đáp án: A

Câu 25:

Tìm các giá trị của tham số m để bất phương trình mx² - (2m - 1)x + 1 < 0

A. $\frac{4 - 2 \sqrt{3}}{4} < m < \frac{4 + 2 \sqrt{3}}{4}$

B. $4 - 2 \sqrt{3} < m < 4 + 2 \sqrt{3}$

C. Không tồn tại m

D. $\frac{4 - 2 \sqrt{3}}{4} < m < 0$

Xem đáp án

Đáp án: C

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Đại số - Chương 4: Bất đẳng thức. Bất phương trình

Bài 5: Dấu của tam thức bậc hai - SBT Đại số 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương