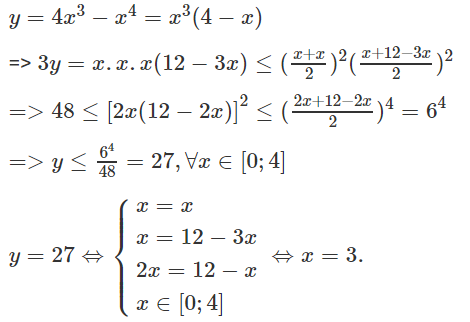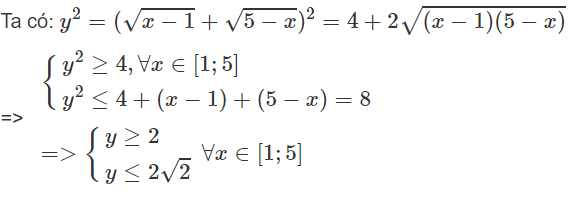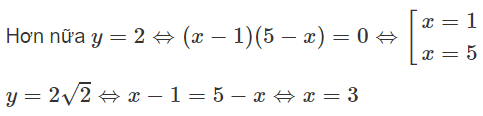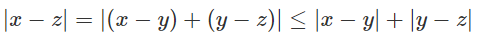18 câu hỏi trắc nghiệm thuộc Bài 1: Bất đẳng thức - SBT Đại số 10

Giải SBT Toán 10 Đại số - Chương 4: Bất đẳng thức. Bất phương trình

Bài 1: Bất đẳng thức - SBT Đại số 10

1602 lượt thi
18 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$x^{4} + y^{4} \geq x^{3} y + {xy}^{3}$

Xem đáp án

Câu 2:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$x^{2} + 4 y^{2} + 3 z^{2} + 14 > 2 x + 12 y + 6 z$

Xem đáp án

Câu 3:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$\frac{1}{a} + \frac{1}{b} \geq \frac{4}{a + b}$

Xem đáp án

Câu 4:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d} \geq \frac{16}{a + b + c + d}$

Xem đáp án

Câu 5:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$a^{2} b + \frac{1}{b} \geq 2 a$

Xem đáp án

Câu 6:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$(a + b) (b + c) (c + a) \geq 8 abc$

Xem đáp án

Câu 7:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

${(\sqrt{a} + \sqrt{b})}^{2} \geq \sqrt[2]{2 (a + b) \sqrt{ab}}$

Xem đáp án

Câu 8:

Cho a, b, c, d là những số dương; x, y, z là những số thực tùy ý. Chứng minh rằng:

$\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \geq \frac{9}{a + b + c}$

Xem đáp án

Câu 9:

Tìm giá trị nhỏ nhất của hàm số

$y = \frac{4}{x} + \frac{9}{1 - x} với 0 < x < 1$

Xem đáp án

Đẳng thức y = 25 xảy ra khi và chỉ khi

hay x = 2/5

Vậy giá trị nhỏ nhất của hàm số đã cho bằng 25 đạt tại x = 2/5

Câu 10:

Tìm giá trị lớn nhất của hàm số

$y = 4 x^{3} - x^{4} với 0 \leq x \leq 4$

Xem đáp án

Vậy giá trị lớn nhất của hàm số đã cho bằng 27 đạt được khi x = 3.

Câu 11:

Tìm giá trị lớn nhất, nhỏ nhất của hàm số sau trên tập xác định của nó

$y = \sqrt{x - 1} + \sqrt{5 - x}$

Xem đáp án

Vế phải có nghĩa khi 1 ≤ x ≤ 5

Vậy giá trị lớn nhất của hàm số đã cho bằng 2√2 khi x = 3, giá trị nhỏ nhất của hàm số đã cho bằng 2 khi x = 1 hoặc x = 5.

Câu 12:

Chứng minh rằng:

$|x - z| \leq |x - y| + |y - z|, \forall x, y, z$

Xem đáp án

Câu 13:

Trong các khẳng định sau đây, khẳng định nào đúng?

A. a < b ⇒ ac < bc

B. a < b ⇒ 1/a > 1/b

C. a < b ⇒ a2 < b2

D. a < b ⇒ $a^{3} < b^{3}$

Xem đáp án

A sai khi c ≤ 0; B sai, chẳng hạn khi a < 0 < b; C sai chẳng hạn khi a < b < 0.

Đáp án: D

Câu 14:

Trong các khẳng định sau đây, khẳng định nào sai?

A. |x| ≥ 0, ∀ x

B. |x| + x ≥ 0, ∀ x

C. |x| ≥ a, ⇒ x ≥ a

D. |x| - x ≥ 0, ∀ x

Xem đáp án

A, B, D đúng theo các tính chất của giá trị tuyệt đối, do đó C sai.

Đáp án: C

Câu 15:

Trong các khẳng định sau đây, khẳng định nào đúng?

A. $a < b \Rightarrow \sqrt[3]{a} < \sqrt[3]{b}$

B. $a < b \Rightarrow \sqrt{a} < \sqrt{b}$

C. $a < b \Rightarrow a^{2} < b^{2}$

D. $a < b \Rightarrow \frac{1}{a} > \frac{1}{b}$

Xem đáp án

B, C, D sai khi chẳng hạn khi a < b < 0.

Đáp án: A

Câu 16:

Cho hàm số y = f(x) với tập xác định D. Trong các phát biểu sau đây phát biểu nào đúng?

A. Giá trị lớn nhất của hàm số đã cho là số lớn hơn mọi giá trị của hàm số.

B. Nếu f(x) ≤ M, ∀x ∈ D thì M là giá trị lớn nhất của hàm số y = f(x)

C. Số M = f(x0) trong đó x0 ∈ D là giá trị lớn nhất của hàm số y = f(x) nếu M > f(x), ∀x ∈ D

D. Nếu tồn tại x0 ∈ D sao cho M = f(x0) và M ≥ f(x),∀x ∈ D thì M là giá trị lớn nhất của hàm số đã cho.

Xem đáp án

Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f(x_o), x_o ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.

Đáp án: D

Câu 17:

Tìm giá trị lớn nhất của hàm số sau trên [-1; 1]

$y = \sqrt{1 - x} + \sqrt{1 + x}$

A. max y = 0

B. max y = 2

C. max y = 4

D. max y = √2

Xem đáp án

Tập xác định -1 ≤ x ≤ 1, do đó 1 – x ≤ 2, 1 + x ≤ 2 ⇒ √(1-x) + √(1+x) ≤ 2√2 < 4 nên C sai; Ngoài ra vì 0 và √2 đều nhỏ hơn 2 nên chỉ cần xét xem 2 có phải là giá trị của hàm số không, dễ thấy khi x = 0 thì y = 2. Vậy max y = 2

Đáp án: B

Câu 18:

Tìm giá trị nhỏ nhất của hàm số $y = \frac{1}{x} + \frac{1}{1 - x}$ với tập xác định D = (0; 1)

A. $\underset{x \in D}{\min y} = 4$

B. $\underset{x \in D}{\min y} = \frac{1}{2}$

C. $\underset{x \in D}{\min y} = 2$

D. $\underset{x \in D}{\min y} = 16$

Xem đáp án

Do 0 < x < 1 nên 1/x > 1, 1/(1-x) > 1 suy ra y > 2, ∀x ∈ D, do chọn B và C sai. Mặt khác, dễ thấy khi x = 1/2 thì y = 4 suy ra D sai

Đáp án: A

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Đại số - Chương 4: Bất đẳng thức. Bất phương trình

Bài 1: Bất đẳng thức - SBT Đại số 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương