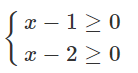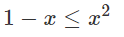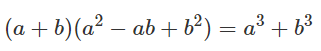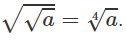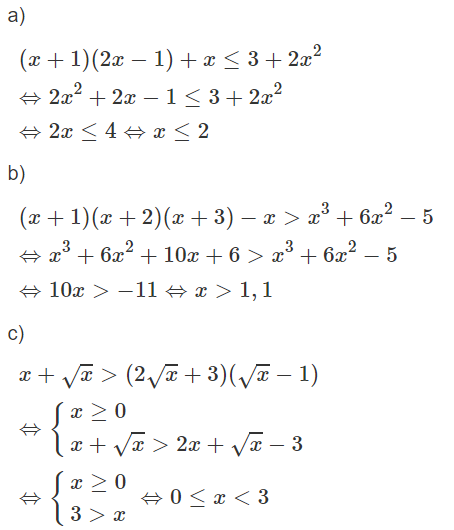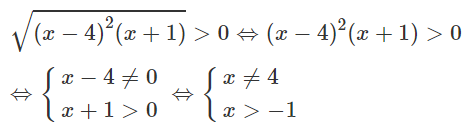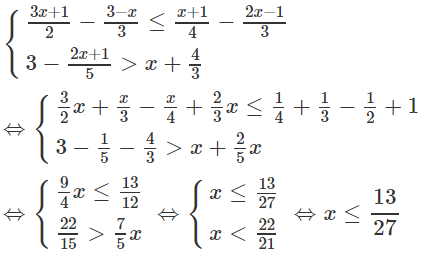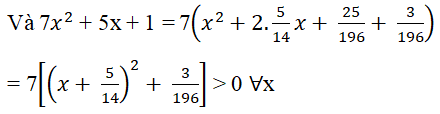15 câu hỏi trắc nghiệm thuộc Bài 2: Bất phương trình và hệ bất phương trình một ẩn - SBT Đại số 10

Câu 1:

Viết điều kiện của mỗi bất phương trình sau:

a) $2 x - 3 - \frac{1}{x - 5} < x^{2} - x$

b) $x^{3} \leq 1$

c) $\sqrt{x^{2} - x - 2} < \frac{1}{2}$

d) $\sqrt[3]{x^{4} + x - 1} + x^{2} - 1 \geq 0$

Xem đáp án

a) Điều kiện là x ≠ 5.

b) Điều kiện là x tùy ý.

c) Điều kiện là x² - x - 2 ≥ 0

d) Điều kiện là x tùy ý.

Câu 2:

Chứng tỏ rằng x = -7 không phải là nghiệm của bất phương trình $x + 3 - \frac{1}{x + 7} < 2 - \frac{1}{x + 7}$ nhưng lại là nghiệm của bất phương trình x + 3 < 2.

Xem đáp án

Làm hai vế của bất phương trình đầu vô nghĩa nên x = -7 không là nghiệm của bất phương trình đó. Mặt khác, x = -7 thỏa mãn bất phương trình sau nên x = -7 là nghiệm của bất phương trình này.

Nhận xét: Phép giản ước số hạng 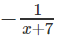ở hai vế của bất phương trình đầu làm mở rộng tập xác định của bất phương trình đó, vì vậy có thể dẫn đến nghiệm ngoại lai.

Câu 3:

Xét xem x = -3 là nghiệm của bất phương trình nào trong hai bất phương trình sau

3x + 1 < x + 3 (1) và (3x + 1)² < (x + 3)² (2)

Từ đó suy ra rằng phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.

Xem đáp án

Thử trực tiếp ta thấy ngay x = -3 là nghiệm của bất phương trình (1) nhưng không là nghiệm bất phương trình (2), vì vậy (1) và (2) không tương đương do đó phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.

Câu 4:

Tìm điều kiện của mỗi bất phương trình đã cho sau đây rồi cho biết các bất phương trình này có tương đương đương với nhau hay không:

$\sqrt{(x - 1) (x - 2)} \geq x (1) và \sqrt{x - 1} . \sqrt{x - 2} \geq x (2)$

Xem đáp án

Điều kiện của (1) và điều kiện của (2) là

Hai bất phương trình đã cho không tương đương với nhau vì có x = -1 là một nghiệm của (1) nhưng không là nghiệm của (2).

Nhận xét:Phép biến đổi đồng nhất 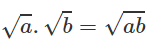làm mở rộng tập xác định, dẫn tới thay đổi điều kiện của phương trình, do đó có thể làm xuất hiện nghiệm ngoại lai.

Câu 5:

Nếu nhân hai vế bất phương trình 1/x ≤ 1 với x ta được bất phương trình nào? Bất phương trình nhận được có tương đương với bất phương trình đã cho hay không? Vì sao?

Xem đáp án

Nếu nhân hai vế của 1/x ≤ 1 với x, ta được bất phương trình mới x ≥ 1; bất phương trình này không tương đương với bất phương trình đã cho vì đã làm mất đi tất cả các nghiệm âm của nó.

Ghi nhớ: Không được nhân hay chia hai vế của một bất phương trình với một biểu thức chứa ẩn mà không biết dấu của biểu thức đó.

Câu 6:

Nếu bình phương hai vế (khử căn thức chứa ẩn) của bất phương trình $\sqrt{1 - x} \leq x$ ta nhận được bất phương trình nào? Bất phương trình nhận được có tương đương với bất phương trình đã cho hay không? Vì sao?

Xem đáp án

Nếu bình phương hai vế (khử căn thức chứa ẩn) của bất phương trình ta nhận được bất phương trình

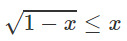
Bất phương trình nhận được không tương đương với bất phương trình đã cho vì có x = 2 không phải là nghiệm bất phương trình đã cho nhưng lại là nghiệm của bất phương trình mới nhận được sau phép bình phương.

Ghi nhớ: Không được bình phương hai vế một bất phương trình vì có thể làm xuất hiện nghiệm ngoại lai.

Câu 7:

a) $x^{2} + \frac{1}{x^{2} + 1} < 1$

b) $\sqrt{x^{2} - x + 1} + \frac{1}{\sqrt{x^{2} - x + 1}} < 2$

c) $\sqrt{x^{2} + 1} + \sqrt{x^{4} - x^{2} + 1} < 2 \sqrt[4]{x^{6} + 1}$

Xem đáp án

a) Theo bất đẳng thức Cô – si ta có:

Vì vậy bất phương trình đã cho vô nghiệm.

b) Tương tự a)

(sử dụng bất đẳng thức)

và đồng nhất thức

Câu 8:

Giải các bất phương trình sau:

a) $(x + 1) (2 x - 1) + x \leq 3 + 2 x^{2}$

b) $(x + 1) (x + 2) (x + 3) - x > x^{3} + 6 x^{2} - 5$

c) $x + \sqrt{x} > (2 \sqrt{x} + 3) (\sqrt{x} - 1)$

Xem đáp án

Câu 9:

Giải các bất phương trình sau:

a) $\sqrt{{(x - 4)}^{2} (x + 1)} > 0$

b) $\sqrt{{(x + 2)}^{2} (x - 3)} > 0$

Xem đáp án

a)

Tập nghiệm của bất phương trình là: (-1; 4)∪(4; +∞)

b) Đáp số: x > 3.

Câu 10:

Giải các bất phương trình sau:

$\{\begin{cases} \frac{3 x + 1}{2} - \frac{3 - x}{3} \leq \frac{x + 1}{4} - \frac{2 x - 1}{3} \\ 3 - \frac{2 x + 1}{5} > x + \frac{4}{3} \end{cases}$

Xem đáp án

Câu 11:

Giải và biện luận bất phương trình theo tham số m.

mx - m² > 2x - 4

Xem đáp án

mx - m² > 2x - 4 ⇔ (m - 2)x > (m - 2)(m + 2)

Nếu m > 2 thì m – 2 > 0, bất phương trình có nghiệm là x > m + 2;

Nếu m < 2 thì m – 2 < 0, bất phương trình có nghiệm là x < m + 2;

Nếu m = 2 thì bất phương trình trở thành 0x > 0, bất phương trình vô nghiệm.

Câu 12:

Trong các khẳng định sau đây, khẳng định nào đúng?

A. Nếu cộng hai vế của một bất phương trình với cùng một số thì ta được một bất phương trình tương đương với bất phương trình đã cho.

B. Nếu nhân hai vế của một bất phương trình với cùng một số thì ta được một bất phương trình tương đương với bất phương trình đã cho.

C. Nếu chia hai vế của một bất phương trình với cùng một số thì ta được một bất phương trình tương đương với bất phương trình đã cho.

D. Nếu bình phương hai vế của một bất phương trình với cùng một số thì ta được một bất phương trình mới tương đương với bất phương trình đã cho.

Xem đáp án

Sử dụng tính chất “cộng hay trừ hai vế một bất đẳng thức với cùng một số và giữ nguyên chiều bất đẳng thức ta được một bất đẳng thức tương đương”.

Đáp án: A

Câu 13:

Trong các bất phương trình sau đây, bất phương trình nào có nghiệm?

A. $\sqrt{2 - x} + \sqrt{x - 4}$

B. $\sqrt{4 - x} (\sqrt{x} + 2) \sqrt{x - 9} < x + 1$

C. $\sqrt{x^{2} + 1} + \sqrt{x^{4} - x^{2} + 1} \geq 2 \sqrt{x^{6} + 1}$

D. $\sqrt{x^{2} + 1} + \sqrt{x^{4} - x^{2} + 1} < 2 \sqrt{x^{6} + 1}$

Xem đáp án

Dễ thấy bất phương trình trong phương án C đúng với x = 0

Đáp án: C

Câu 14:

Trong các khẳng định sau đây, khẳng định nào đúng?

A. $x + 3 - \frac{1}{x + 7} < 2 - \frac{1}{x + 7} \Leftrightarrow x + 3 < 2$

B. $3 x + 1 < x + 3 \Rightarrow {(3 x + 1)}^{2} < {(x + 3)}^{2}$

C. $\sqrt{(x - 1) (x - 2)} \geq x \Leftrightarrow \sqrt{x - 1} . \sqrt{x - 2} \geq x$

D. $7 x^{3} + 12 x^{2} + 6 x + 1 > 0 \Leftrightarrow 2 x + 1 > x$

Xem đáp án

Có 7x³ + 12x² + 6x + 1 = (x + 1)(7x² + 5x + 1)

Nên bất phương trình 7x³ + 12x² + 6x + 1 > 0 ⇔ x + 1 > 0 ⇔ 2x + 1 > x.

Đáp án: D

Câu 15:

Tập nghiệm của bất phương trình sau là:

$\sqrt{{(x - 4)}^{2} (x + 1)} > 0$

A. S = (-1; 4) ∪ (4; +∞)

B. S = [4; +∞)

C. S = [-1; +∞)

D. S = (-1; +∞)

Xem đáp án

Khi x = 4 căn thức triệt tiêu nên x = 4 không là nghiệm của bất phương trình, do đó B, C, D đều sai.

Đáp án: A

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 10 Đại số - Chương 4: Bất đẳng thức. Bất phương trình

Bài 2: Bất phương trình và hệ bất phương trình một ẩn - SBT Đại số 10

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương