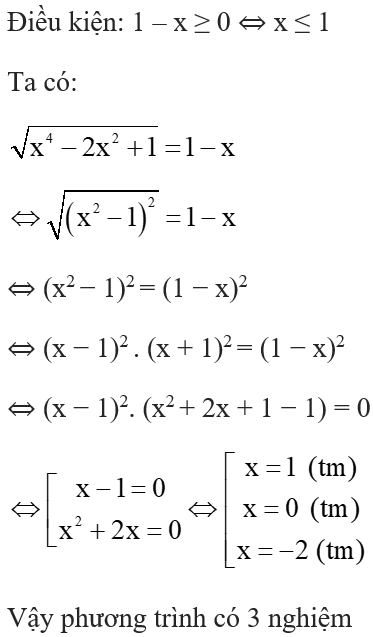15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Phương trình quy về phương trình bậc nhất, bậc hai có đáp án (Thông hiểu)

Câu 1:

Biết rằng phương trình x²− 4x + m + 1 = 0 có một nghiệm bằng 3. Nghiệm còn lại của phương trình bằng:

A. -1

B. 1

C. 2

D. 4

Xem đáp án

Đáp án cần chọn là: B

Vì phương trình đã cho có nghiệm bằng 3 nên thay x = 3 vào phương trình, ta được

9 – 12 + m + 1 = 0 ⇔ m = 2.

Với m = 2 phương trình trở thành x²– 4x + 3 = 0 ⇔ $[\begin{matrix} x = 3 \\ x = 1 \end{matrix}$

Câu 2:

Cho phương trình ax²+ bx + c = 0 (1). Đặt $S = - \frac{b}{a}, P = \frac{c}{a}$ , hãy chọn khẳng định sai trong các khẳng định sau:

A. Nếu P < 0 thì (1) có 2 nghiệm trái dấu

B. Nếu P > 0 và S < 0 thì (1) có 2 nghiệm

C. Nếu P > 0 và S < 0 và Δ > 0 thì (1) có 2 nghiệm âm phân biệt.

D. Nếu P > 0 và S > 0 và Δ > 0 thì (1) có 2 nghiệm dương phân biệt

Xem đáp án

Đáp án cần chọn là: B

Đáp án A: Nếu P < 0 ⇒ ac < 0 nên phương trình có hai nghiệm trái dấu.

Đáp án B: Ta xét phương trình x²+ x + 1 = 0 có P = 1 > 0, S < 0 nhưng lại vô nghiệm nên B sai.

Đáp án C, D: Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt. Khi đó S, P lần lượt là tổng và tích hai nghiệm của phương trình. Do đó:

+) Nếu P > 0 và S < 0 thì (1) có 2 nghiệm âm phân biệt.

+) Nếu P > 0 và S > 0 thì (1) có 2 nghiệm dương phân biệt.

Câu 3:

Phương trình (m²− 2m)x = m²− 3m + 2 có nghiệm khi:

A. m = 0

B. m = 2

C. m ≠ 0 và m ≠ 2

D. m ≠ 0

Xem đáp án

Đáp án cần chọn là: D

Phương trình có nghiệm khi và chỉ khi:

$[\begin{matrix} m^{2} - 2 m \neq 0 \\ m^{2} - 2 m = m^{2} - 3 m + 2 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} \{\begin{matrix} m \neq 0 \\ m \neq 2 \end{matrix} \\ m = 2 \end{matrix} \Leftrightarrow m \neq 0$

Câu 4:

Cho phương trình m²x + 6 = 4x + 3m. Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.

A. m = 2

B. m ≠ −2

C. m ≠ −2 và m ≠ 2

D. m ∈ R

Xem đáp án

Đáp án cần chọn là: B

Phương trình viết lại (m²− 4)x = 3m − 6.

Phương trình đã cho vô nghiệm khi $\{\begin{matrix} m^{2} - 4 = 0 \\ 3 m - 6 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} m = \pm 2 \\ m \neq 2 \end{matrix} \Leftrightarrow m = - 2$

Do đó, phương trình đã cho có nghiệm khi m ≠ −2.

Câu 5:

Phương trình $x^{4} + (1 - \sqrt{3}) x^{2} + 2 (4 - 2 \sqrt{3}) = 0$ có bao nhiêu nghiệm?

A. 2

B. 3

C. 4

D. 0

Xem đáp án

Đáp án cần chọn là: D

Đặt $x^{2} = t \geq 0$ ta được $t^{2} + (1 - \sqrt{3}) t + 2 (4 - 2 \sqrt{3}) = 0$

Ta có $Δ = {(1 - \sqrt{3})}^{2} - 4.2 (4 - 2 \sqrt{3})$

$= 4 - 2 \sqrt{3} - 8 (4 - 2 \sqrt{3}) = - 7 (4 - 2 \sqrt{3}) < 0$

Suy ra phương trình ẩn t vô nghiệm hay phương trình đã cho cũng vô nghiệm.

Câu 6:

Phương trình sau có bao nhiêu nghiệm âm: $x^{4} - 2005 x^{2} - 13 = 0$

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án cần chọn là: B

Đặt t = x²(t ≥ 0)

Phương trình (1) thành $t^{2} - 2005 t - 13 = 0 (2)$

Phương trình (2) có $a . c = 1. (- 13) < 0$

Suy ra phương trình (2) có 2 nghiệm trái dấu

Do đó phương trình (1) có một nghiệm âm và một nghiệm dương

Câu 7:

Phương trình: $2 x^{4} - 2019 x^{2} - 6 = 0$ có bao nhiêu nghiệm dương?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án cần chọn là: B

Đặt t = x²(t ≥ 0)

Phương trình (1) thành $2 t^{2} - 2019 t - 6 = 0 (1)$

Phương trình (2) có $a . c = 2. (- 6) < 0$

Suy ra phương trình (2) có 2 nghiệm trái dấu

Do đó phương trình (1) có một nghiệm âm và một nghiệm dương

Câu 8:

Tập nghiệm S của phương trình $\frac{(m^{2} + 1) x - 1}{x + 1} = 1$ trong trường hợp $m \neq 0$ là:

A. $S = \{\frac{m + 1}{m^{2}}\}$

B. $S = \emptyset$

C. $S = R$

D. $S = \{\frac{2}{m^{2}}\}$

Xem đáp án

Đáp án cần chọn là: D

$\frac{(m^{2} + 1) x - 1}{x + 1} = 1 \Leftrightarrow \{\begin{matrix} x \neq - 1 \\ (m^{2} + 1) x - 1 = x + 1 \end{matrix} \Leftrightarrow x = \frac{2}{m^{2}}$

Dễ thấy $x = \frac{2}{m^{2}} > 0, \forall m \neq 0$ nên $x \neq - 1$

Câu 9:

Tổng các nghiệm của phương trình $|2 x - 5| + |2 x^{2} - 7 x + 5| = 0$ bằng:

A. 6

B. $\frac{5}{2}$

C. $\frac{7}{2}$

D. $\frac{3}{2}$

Xem đáp án

Đáp án cần chọn là: B

Ta có $\{\begin{matrix} |2 x - 5| \geq 0 \\ |2 x^{2} - 7 x + 5| \geq 0 \end{matrix} \Rightarrow$ $|2 x - 5| + |2 x^{2} - 7 x + 5| \geq 0$

Dấu “=” xảy ra khi và chỉ khi $\{\begin{matrix} 2 x - 5 = 0 \\ 2 x^{2} - 7 x + 5 = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x = \frac{5}{2} \\ x = 1 \lor x = \frac{5}{2} \end{matrix} \Leftrightarrow x = \frac{5}{2}$

Câu 10:

Tập nghiệm T của phương trình: $\frac{|x - 3|}{\sqrt{x - 4}} = \frac{x - 3}{\sqrt{x - 4}}$ là:

A. T = [3; +∞)

B. T = [4; +∞)

C. T = (4; +∞)

D. T = ∅

Xem đáp án

Đáp án cần chọn là: C

Điều kiện: x > 4

Phương trình trở thành: $|x - 3| = x - 3 \Leftrightarrow \{\begin{matrix} x - 3 \geq 0 \\ [\begin{matrix} x - 3 = x - 3 \\ x - 3 = 3 - x \end{matrix} \end{matrix} \Leftrightarrow \{\begin{matrix} x \geq 3 \\ [\begin{matrix} 0 x = 0 \\ x = 3 \end{matrix} \end{matrix} \Leftrightarrow x \geq 3$

Vậy T = (4; +∞).

Câu 11:

Tìm số nghiệm của phương trình sau $\sqrt{2 x - 3} = \sqrt{4 x^{2} - 15}$

A. 1 nghiệm duy nhất

B. vô nghiệm

C. 3 nghiệm

D. 5 nghiệm

Xem đáp án

Đáp án cần chọn là: A

ĐKXĐ: $\{\begin{matrix} 2 x - 3 \geq 0 \\ 4 x^{2} - 15 \geq 0 \end{matrix} (*)$

Với điều kiện (*) phương trình tương đương với

${(\sqrt{2 x - 3})}^{2} = {(\sqrt{4 x^{2} - 15})}^{2} \Leftrightarrow 2 x - 3 = 4 x^{2} - 15$

$\Leftrightarrow 4 x^{2} - 2 x - 12 = 0 \Leftrightarrow [\begin{matrix} x = 2 \\ x = - \frac{3}{2} \end{matrix}$

Thay vào điều kiện (*) ta thấy chỉ có x = 2 thỏa mãn

Vậy phương trình có nghiệm duy nhất x = 2

Câu 12:

Tập nghiệm của phương trình $\sqrt{x - 2} - \frac{x + 5}{\sqrt{7 - x}} = 0$ là:

A. {2}

B. ∅

C. {7}

D. {2; 7}

Xem đáp án

Đáp án cần chọn là: B

Điều kiện: $\{\begin{matrix} x - 2 \geq 0 \\ 7 - x > 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \geq 2 \\ x < 7 \end{matrix} \Leftrightarrow 2 \leq x < 7$

Khi đó x + 5 > 0 nên phương trình $\Leftrightarrow \sqrt{(x - 2) (7 - x)} = x + 5$

$\Leftrightarrow - x^{2} + 9 x - 14 = x^{2} + 10 x + 25$

$\Leftrightarrow 2 x^{2} + x + 39 = 0$ , có $Δ = - 311 < 0$ nên phương trình vô nghiệm

Câu 13:

Số nghiệm của phương trình $\sqrt{x^{4} - 2 x^{2} + 1} = 1 - x$ là:

A. 0

B. 3

C. 2

D. 1

Xem đáp án

Đáp án cần chọn là: B

Câu 14:

Cho hai hàm số y = (m + 1)x²+ 3m²x + m và y = (m + 1)x²+ 12x + 2. Tìm tất cả các giá trị của tham số m để đồ thị hai hàm số đã cho không cắt nhau.

A. m = 2

B. m = −2

C. m = ±2

D. m = 1

Xem đáp án

Đáp án cần chọn là: B

Đồ thị hai hàm số không cắt nhau khi và chỉ khi phương trình

(m + 1)x²+ 3m²x + m = (m + 1)x²+ 12x + 2 vô nghiệm

⇔ 3(m²− 4)x = 2 − m vô nghiệm

$\Leftrightarrow \{\begin{matrix} m^{2} - 4 = 0 \\ 2 - m \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} m = \pm 2 \\ m \neq 2 \end{matrix} \Leftrightarrow m = - 2$

Câu 15:

Cho phương trình ax⁴+ bx²+ c = 0 (1) (a ≠ 0).

Đặt: Δ = b²− 4ac, $S = \frac{- b}{a}, P = \frac{c}{a}$ . Ta có (1) vô nghiệm khi và chỉ khi:

A. $Δ < 0$

B. $Δ < 0 \lor \{\begin{matrix} Δ \geq 0 \\ S < 0 \\ P > 0 \end{matrix}$

C. $\{\begin{matrix} Δ > 0 \\ S < 0 \end{matrix}$

D. $\{\begin{matrix} Δ > 0 \\ P > 0 \end{matrix}$

Xem đáp án

Đáp án cần chọn là: B

Đặt t = x²(t ≥ 0)

Phương trình (1) thành at²+ bt + c = 0 (2)

Phương trình (1) vô nghiệm

⇔ Phương trình (2) vô nghiệm hoặc phương trình (2) có 2 nghiệm cùng âm

⇔ Δ < 0 hoặc $\{\begin{matrix} Δ \geq 0 \\ S < 0 \\ P > 0 \end{matrix}$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Phương trình quy về phương trình bậc nhất, bậc hai có đáp án

Trắc nghiệm Phương trình quy về phương trình bậc nhất, bậc hai có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương