Đáp án cần chọn là: C

Phương trình ax + b = 0 có nghiệm nếu nó có nghiệm duy nhất hoặc vô số nghiệm.

- Phương trình ax + b = 0 có nghiệm duy nhất nếu a ≠ 0.

- Phương trình ax + b = 0 vô số nghiệm nếu a = b = 0.

Vậy phương trình ax + b = 0 có nghiệm nếu  $\left[\begin{array}{c}a=b=0\\ a\pm 0\end{array}\right.$

Đáp án cần chọn là: B

Phương trình ax² + bx + c = 0(a > 0) có nghiệm duy nhất nếu

 Δ = b² − 4ac = 0 ⇔ b² = 4ac.

Đáp án cần chọn là: A

Phương trình m²x + m – 3 = 0 là phương trình bậc nhất khi và chỉ khi:

a = m² ≠ 0 ⇔ m ≠ 0

Đáp án cần chọn là: C

Điều kiện:  $x\ne 1$

Phương trình:$2x+\frac{3}{x-1}=\frac{3x}{x-1}$ $\iff 2x(x-1)+3=3x\iff 2x^2-5x+3=0$

  $\iff \left[\begin{array}{c}x=1\left(l\right)\\ x=\frac{3}{2}\left(n\right)\end{array}\right.$

Vậy $S=\left\{\frac{3}{2}\right\}$

Đáp án cần chọn là: B

Phương trình  $\iff \left\{\begin{array}{c}x+4\ge 0\\ {\left(x^2+5x+4\right)}^2={\left(x+4\right)}^2\end{array}\right.$

$\iff \left\{\begin{array}{c}x\ge -4\\ {\left(x^2+5x+4\right)}^2-{\left(x+4\right)}^2=0\end{array}\right.$

$\begin{array}{l}\iff \left\{\begin{array}{c}x\ge -4\\ (x^2+6x+8)(x^2+4x)=0\end{array}\right.\iff \left\{\begin{array}{c}x\ge -4\\ \left[\begin{array}{c}{x}^2+6x+8=0\\ x^2+4x=0\end{array}\right.\end{array}\right.\\ \iff \left\{\begin{array}{c}x\ge -4\\ \left[\begin{array}{c}x=-2,x=-4\\ x=0,x=-4\end{array}\right.\end{array}\right.\iff \left[\begin{array}{c}x=0\\ x=-2\\ x=-4\end{array}\right.\\ \Rightarrow 0+(-2)+(-4)=-6\end{array}$

Đáp án cần chọn là: D

Ta có: ; $\frac{x^2}{2}-2x+\frac{3}{2}=0\iff \left[\begin{array}{c}x=1\\ x=3\end{array}\right.$ ;    $\frac{x^2}{2}-3x+4=0\iff \left[\begin{array}{c}x=2\\ x=4\end{array}\right.$     

Từ đó ta phá dấu giá trị tuyệt đối của mỗi biểu thức như sau:

TH1:  $x\le 1$

Phương trình thành:$\frac{x^2}{2}-2x+\frac{3}{2}$ +  $\frac{x^2}{2}-3x+4$$=\frac{3}{4}$$\iff x^2-5x+\frac{19}{4}=0$

$\iff \left[\begin{array}{c}x=\frac{5+\sqrt{6}}{2}\left(l\right)\\ x=\frac{5-\sqrt{6}}{2}\left(l\right)\end{array}\right.$

TH2: 1 < x < 2

Phương trình thành:$-\frac{x^2}{2}+2x-\frac{3}{2}$  +  $\frac{x^2}{2}-3x+4$$=\frac{3}{4}$$\iff x=\frac{7}{4}\left(n\right)$

TH3:  $2\le x\le 3$

Phương trình thành:$-\frac{x^2}{2}+2x-\frac{3}{2}$  -  $\frac{x^2}{2}+3x-4$$=\frac{3}{4}$$\iff -x^2+5x-\frac{25}{4}=0$

$\iff x=\frac{5}{2}\left(n\right)$

TH4: 3 < x < 4

Phương trình thành:$\frac{x^2}{2}-2x+\frac{3}{2}$  -   $\frac{x^2}{2}+3x-4$$=\frac{3}{4}$$\iff x=\frac{13}{4}\left(n\right)$

TH5:  $x\ge 4$

Phương trình thành: $\frac{x^2}{2}-2x+\frac{3}{2}$ +$\frac{x^2}{2}-3x+4$$=\frac{3}{4}$$\iff x^2-5x+\frac{19}{4}=0$  

$\iff \left[\begin{array}{c}x=\frac{5+\sqrt{6}}{2}\left(l\right)\\ x=\frac{5-\sqrt{6}}{2}\left(l\right)\end{array}\right.$

Vậy $x=\text{}\frac{7}{4},x=\frac{5}{2},x=\frac{13}{4}$

Đáp án cần chọn là: B

Phương trình có hai nghiệm phân biệt khi Δ > 0.

Khi đó, gọi hai nghiệm của phương trình là x₁ và x₂.

Do x₁ và x₂ là hai nghiệm dương nên $\left\{\begin{array}{c}{x}_1+x_2>0\\ x_1{x}_2>0\end{array}\right.$ hay  $\left\{\begin{array}{c}S>0\\ P>0\end{array}\right.$

Đáp án cần chọn là: D

Phương trình đã cho nghiệm đúng với $\forall x\in R$ hay phương trình có vô số nghiệm khi

$\left\{\begin{array}{c}{m}^2-3m+2=0\\ -(m^2+4m+5)=0\end{array}\right.\iff \left\{\begin{array}{c}\left[\begin{array}{c}m=1\\ m=2\end{array}\right.\\ m\in \varnothing \end{array}\right.\iff m\in \varnothing$

Đáp án cần chọn là: A

Với m = 1 ta được phương trình 3x – 1 = 0 ⇔$x=\frac{1}{3}$

Với m ≠ 1 Phương trình  có  nghiệm khi  3² + 4(m − 1) ≥ 0 ⇔$m\ge -\frac{5}{4}$

Đáp án cần chọn là: D

Ta có: (x − 1)(x² − 4mx − 4) = 0  $\iff \left[\begin{array}{c}x=1\\ x^2-4mx-4=0\end{array}\right.$

Phương trình có 3 nghiệm phân biệt khi x² − 4mx – 4 = 0 có 2 nghiệm phân biệt khác 1

$\iff \left\{\begin{array}{c}{\Delta }^{\text{'}}>0\\ f\left(1\right)\ne 0\end{array}\right.\iff \left\{\begin{array}{c}4m^2+4>0\\ -4m-3\ne 0\end{array}\right.\iff m\ne -\frac{3}{4}$

Đáp án cần chọn là: C

Phương trình có hai nghiệm phân biệt ⇔ Δ′ > 0

⇔ m² − 7m + 16 > 0 ⇔  ${\left(m-\frac{7}{2}\right)}^2+\frac{15}{4}>0,\forall m\in R$

Theo định lí Viet, ta có $\left\{\begin{array}{c}{x}_1.x_2=\frac{3m-5}{3};x_1+x_2=\frac{2(m+1)}{3}\\ x_1=3x_2\end{array}\right.$
$\iff \left\{\begin{array}{c}{x}_1=\frac{m+1}{2},x_2=\frac{m+1}{6}\\ x_1.x_2=\frac{3m-5}{3}\end{array}\right.$

 $\Rightarrow \frac{{\left(m+1\right)}^2}{12}=\frac{3m-5}{3}\iff m^2-10m+21=0\iff \left[\begin{array}{c}m=3\\ m=7\end{array}\right.$

Đáp án cần chọn là: D

Phương trình (m² − m)x + m – 3 = 0 là phương trình bậc nhất khi và chỉ khi:

a = m² – m ≠ 0 ⇔  $\left\{\begin{array}{c}m\ne 1\\ m\ne 0\end{array}\right.$

Đáp án cần chọn là: D

Phương trình hoành độ giao điểm –x² − 2x + 3 = x² − m

⇔ 2x² + 2x – m – 3 = 0.    (∗)

Để hai đồ thị hàm số có điểm chung khi và chỉ khi phương trình (∗) có nghiệm

⇔ Δ = 1 − 2(−m − 3) ≥ 0 ⇔ m ≥ −$\frac{7}{2}$  

Đáp án cần chọn là: A

c và d là nghiệm của phương trình x² + ax + b = 0  $\Rightarrow \left\{\begin{array}{c}c+d=-a\left(1\right)\\ cd=b\left(2\right)\end{array}\right.$

a, b là nghiệm của phương trình x² + cx  + d = 0  $\Rightarrow \left\{\begin{array}{c}a+b=-c\left(3\right)\\ ab=d\left(4\right)\end{array}\right.$

(3) ; (4) ; (1) ⇒ −a – b + ab = −a ⇒ −b + ab = 0 ⇒ a = 1

(3) ; (4) ; (2)  ⇒ (a + b) ab = −b ⇒  (a + b) a = −1 ⇒ b = −2 ⇒ c = 1, d = −2

⇒ a + b + c + d = −2

Đáp án cần chọn là: A

Ta có: x² − 2a(x − 1) −1 = 0 ⇔ x² − 2ax + 2a – 1 = 0 ⇔$\left[\begin{array}{c}x=1\\ x=2a\end{array}\right.$

(do 1 + (−2a) + 2a – 1 = 0 )

Yêu cầu bài toán  $x_1+x_2=x_1^2+x_2^2\Rightarrow x_1+x_2={(x_1+x_2)}^2-2x_1{x}_2$

$\Rightarrow 2a=4a^2-4a+2\Rightarrow \left[\begin{array}{c}a=1\\ a=\frac{1}{2}\end{array}\right.$

Đáp án cần chọn là: C

$\left|x_1^4-x_2^4\right|=\left|\left(x_1^2+x_2^2\right)\left(x_1^2-x_2^2\right)\right|=\left[{\left(x_1+x_2\right)}^2-2x_1{x}_2\right]\left|x_1-x_2\right|\left|x_1+x_2\right|$

Mà

$\left|x_1-x_2\right|=\sqrt{{(x_1-x_2)}^2}=\sqrt{{(x_1+x_2)}^2-4x_1{x}_2}=\sqrt{{(2m+2)}^2-4(m^2+2)}=\sqrt{8m-4}$

Suy ra

$\left|x_1^4-x_2^4\right|=\left[{(2m+2)}^2-2(m^2+2)\right]\sqrt{8m-4}\left|2m+2\right|$

$=(2m^2+8)\sqrt{8m-4}\left|2m+2\right|$

Suy ra

$\left|x_1^4-x_2^4\right|=16m^2+64m\iff (2m^2+8m)\sqrt{8m-4}\left|2m+2\right|=16m^2+64m$

$\begin{array}{l}\iff (m^2+4m)\left(\sqrt{8m-4}\left|2m+2\right|-8\right)=0\\ \iff \left[\begin{array}{c}{m}^2+4m=0\left(1\right)\\ \sqrt{8m-4}\left|2m+2\right|=8\left(2\right)\end{array}\right.\end{array}$

Ta có (1) $\iff \left[\begin{array}{c}m=0\\ m=-4\end{array}\right.$ (loại)

(2) ⇔ (8m − 4) (2m + 2)² = 64 ⇔ 32m³ + 48m² – 80 = 0

⇔ m = 1 (thỏa mãn (*))

Vậy m = 1 thỏa mãn yêu cầu bài toán.

Đáp án cần chọn là: B

Phương trình có hai nghiệm ⇔ Δ′ = (m + 1)² − (m² + 2) = 2m + 1 ≥ 0

$\iff m\ge \frac{1}{2}$

$B=\sqrt{2(x_1^2+x_2^2)+16}-3x_1{x}_2$

$\begin{array}{l}=\sqrt{2{(x_1+x_2)}^2-4x_1{x}_2+16}-3x_1{x}_2\\ =\sqrt{2{(2m+2)}^2-4(m^2+2)+16}-3(m^2+2)=\sqrt{4m^2+16m+16}-3(m^2+2)\\ =2m+4-3(m^2+2)=-3m^2+2m-2\end{array}$

Xét hàm số $y=-3m^2+2m-2$ với  $m\ge \frac{1}{2}$

Bảng biến thiên 

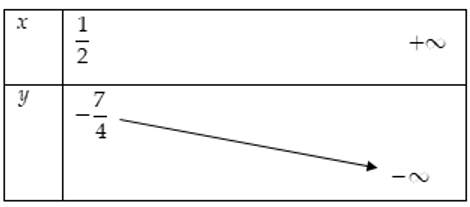
Suy ra giá trị $\underset{m\ge \frac{1}{2}}{max}y=-\frac{7}{4}$ khi  $m=\frac{1}{2}$

Vậy giá trị lớn nhất của biểu thức B là $-\frac{7}{4}$ khi $m=\frac{1}{2}$

Đáp án cần chọn là: A

Ta có = m² + 2 − 2(2m + 2) – 6 = m² − 4m − 8

⇒ A = (m − 2)² – 12 ≥ −12

Suy ra min A = −12 ⇔ m = 2 thỏa mãn (*)

Vậy với m = 2 thì biểu thức A đạt giá trị nhỏ nhất.

Đáp án cần chọn là: C

Gọi x₁, x₂ là nghiệm của phương trình x² - 2mx + 1 = 0. Khi đó $\left\{\begin{array}{c}{x}_1+x_2=2m\\ x_1.x_2=1\end{array}\right.$

Gọi x₁, x₂ là nghiệm của phương trình x² - 2x + m = 0. Khi đó $\left\{\begin{array}{c}{x}_3+x_4=2\\ x_3.x_4=m\end{array}\right.$

Ta có:  $\left\{\begin{array}{c}{x}_1=\frac{1}{x^3}\\ x_2=\frac{1}{x_4}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{c}{x}_1+x_2=\frac{1}{x^3}+\frac{1}{x_4}\\ x_1.x_2=\frac{1}{x_3.x_4}\end{array}\right.\Rightarrow \left\{\begin{array}{c}{x}_1+x_2=\frac{x_3+x_4}{x_3.x_4}\\ x_1.x_2=\frac{1}{x_3.x_4}\end{array}\right.$$\iff \left\{\begin{array}{c}2m=\frac{2}{m}\\ 1=\frac{1}{m}\end{array}\right.\iff m=1$

Đáp án cần chọn là: D

Gọi x₀ là một nghiệm của phương trình x² – mx + 2 = 0.

Suy ra 3 – x₀ là một nghiệm của phương trình x² + 2x − m = 0.

Khi đó, ta có hệ

$\left\{\begin{array}{c}{x}_0^2-m{x}_0+2=0\\ {(3-x_0)}^2+2(3-x_0)-m=0\end{array}\right.$

$\iff \left\{\begin{array}{c}{x}_0^2-m{x}_0+2=0\left(1\right)\\ m=x_0^2-8x_0+15\left(2\right)\end{array}\right.$

Thay (2) vào (1), ta được  $x_0^2-(x_0^2-8x_0+15)x_0+2=0\iff \left[\begin{array}{c}{x}_0=2\\ x_0=\frac{7\pm 3\sqrt{5}}{2}\end{array}\right.$

Cho ta 3 giá trị của m cần tìm.

Đáp án cần chọn là: D

Phương trình đã cho có một nghiệm duy nhất khi x² − 3x + m = 0 vô nghiệm hoặc có nghiệm duy nhất x = 1.

TH1: Phương trình x² − 3x + m = 0 vô nghiệm ⇔ Δ = 3² − 4m < 0 ⇔ m > $\frac{9}{4}$ .

TH2: Phương trình x² − 3x + m = 0 có nghiệm duy nhất x = 1

$\iff \left\{\begin{array}{c}\Delta =0\\ 1^2-3.1+m=0\end{array}\right.\iff \left\{\begin{array}{c}9-4m=0\\ -2+m=0\end{array}\right.\iff \left\{\begin{array}{c}m=\frac{9}{4}\\ m=2\end{array}\right.\Rightarrow m\in \varnothing$

Vậy $m>\frac{9}{4}$

Đáp án cần chọn là: D

Đặt t = x² − 2x + 3 = (x − 1)² + 2  2 ta được phương trình 

t² + 2(3 − m)t + m² − 6m = 0 (1)

Δ′ = m² − 6m + 9 – m² + 6m = 9 suy ra phương trình (1) luôn có hai nghiệm là

 t₁ = m − 6 và t₂ = m

Theo yêu cầu bài toán ta suy ra phương trình (1) có nghiệm lớn hơn hoặc bằng 2

  $\iff \left[\begin{array}{c}m-6\ge 2\\ m\ge 2\end{array}\right.\iff m\ge 2$

Đáp án cần chọn là: A

Đặt t = x² − 2x + 3 = (x − 1)² + 2  2 ta được phương trình 

t² + 2(3 − m)t + m² − 6m = 0 (1)

Δ′ = m² − 6m + 9 – m² + 6m = 9 suy ra phương trình (1) luôn có hai nghiệm là

 t₁ = m − 6 và t₂ = m

Theo yêu cầu bài toán ta suy ra phương trình (1) phải có cả hai nghiệm nhỏ hơn 2

  $\iff \left\{\begin{array}{c}m-6<2\\ m<2\end{array}\right.$$\iff \left\{\begin{array}{c}m<8\\ m<2\end{array}\iff m<2\right.$

Đáp án cần chọn là: A

Đặt t = x² ≥ 0

Phương trình (1) thành t² + 2t + a = 0 (2)

Phương trình (1) có đúng 4 nghiệm

⇔ Phương trình (2) có 2 nghiệm dương phân biệt

 $\iff \left\{\begin{array}{c}\Delta >0\\ S>0\\ P>0\end{array}\right.\iff \left\{\begin{array}{c}4-4a>0\\ -2>0\\ a>0\end{array}\right.\left(vl\right)\iff a\notin \varnothing$

Đáp án cần chọn là: B

Đặt t = x³ thì phương trình x⁶ + 2003x³ – 2005 = 0 trở thành

 t² + 2003t – 2005 = 0

Vì 1. (−2005) < 0 suy ra phương trình ẩn t có 2 nghiệm trái dấu

Suy ra có phương trình đã cho có một nghiệm âm.

Đáp án cần chọn là: D

Đặt t = x² (t ≥ 0)

Phương trình (1) thành at² + bt + c = 0(2)

Phương trình (1) có 4 nghiệm phân biệt

⇔ Phương trình (2) có 2 nghiệm phân biệt dương  $\iff$$\left\{\begin{array}{c}\Delta >0\\ S>0\\ P>0\end{array}\right.$

Đáp án cần chọn là: D

Đặt $x^2=t\ge 0$ ta được  $t^2+\left(\sqrt{65}-\sqrt{3}\right)t+2\left(8+\sqrt{63}\right)=0$

Ta có  $\Delta ={\left(\sqrt{65}-\sqrt{3}\right)}^2-4.2\left(8+\sqrt{63}\right)=4-2\sqrt{195}-8\sqrt{63}<0$

Suy ra phương trình ẩn t vô nghiệm hay phương trình đã cho cũng vô nghiệm.

Đáp án cần chọn là: D

Đặt t = x² (t ≥ 0)

Phương trình (1) thành  $\sqrt{2}.t^2-2(\sqrt{2}+\sqrt{3})t+\sqrt{12}=0\left(2\right)$

Ta có  $\Delta \text{'}=5+2\sqrt{6}-2\sqrt{6}=5$

Ta có  $\left\{\begin{array}{c}\Delta \text{'}=5>0\\ -\frac{-2\left(\sqrt{2}+\sqrt{3}\right)}{\sqrt{2}}=-\frac{b}{a}>0\\ \frac{\sqrt{12}}{\sqrt{12}}=\frac{c}{a}>0\end{array}\right.$

Suy ra phương trình (2) có 2 nghiệm dương phân biệt  $t_{1,2}=\frac{\sqrt{2}+\sqrt{3}\pm \sqrt{5}}{\sqrt{2}}$

Vậy phương trình (1) có 4 nghiệm $x_{1,2}=\pm \sqrt{\frac{\sqrt{2}+\sqrt{3}+\sqrt{5}}{\sqrt{2}}}$

$x_{1,2}=\pm \sqrt{\frac{\sqrt{2}+\sqrt{3}-\sqrt{5}}{\sqrt{2}}}$

Đáp án cần chọn là: B

Đặt t = x² (t ≥ 0)

Phương trình (1) thành t² + t + m = 0 (2)

Phương trình (1) vô nghiệm

⇔ Phương trình (2) vô nghiệm hoặc phương trình (2) có 2 nghiệm âm (có thể là nghiệm kép âm)

$\iff \Delta <0\cup \left\{\begin{array}{c}\Delta \ge 0\\ S<0\\ P>0\end{array}\right.\iff 1-4m<0\cup \left\{\begin{array}{c}1-4m\ge 0\\ -1<0\\ m>0\end{array}\iff m>\frac{1}{4}\right.\cup \left\{\begin{array}{c}m\le \frac{1}{4}\\ m>0\end{array}\right.$

$\iff m>0$

Phương trình có nghiệm  $\iff m\le 0$

Đáp án cần chọn là: D

Ta có:  $\Delta ={\left(4m-3\right)}^2-\mathrm{4.2.}\left(1-2m\right)={\left(4m-1\right)}^2$

$2{\left(x^2+2x\right)}^2-\left(4m-3\right)\left(x^2+2x\right)+1-2m=0\iff \left[\begin{array}{c}{x}^2+2x=\frac{1}{2}\left(1\right)\\ x^2+2x=2m-1\left(2\right)\end{array}\right.$

$\left(1\right)\iff x^2+2x-\frac{1}{2}=0\iff \left[\begin{array}{c}x=\frac{-2+\sqrt{6}}{2}\notin \left[-3;0\right]\\ x=\frac{-2-\sqrt{6}}{2}\in \left[-3;0\right]\end{array}\right.$

(2)$\iff {\left(x+1\right)}^2=2m.$ Phương trình đã cho có đúng 1 nghiệm thuộc đoạn [−3; 0] khi và chỉ khi phương trình (2) có nghiệm nhưng không thuộc đoạn [−3; 0] hoặc vô nghiệm.

Xét (2), nếu m < 0 thì (2) vô nghiệm (thỏa mãn yêu cầu).

+) Nếu m = 0 thì (2) có nghiệm duy nhất x = −1 ∈ [−3; 0] (không thỏa yêu cầu).

+) Nếu m > 0 thì (2) có hai nghiệm phân biệt $x_1=-1-2\sqrt{m}<-1+2\sqrt{m}=x_2$  nên (2) có hai nghiệm không thuộc [−3; 0] nếu

$\left\{\begin{array}{c}-1-\sqrt{2m}<-3\\ -1+\sqrt{2m}>0\end{array}\right.\iff \left\{\begin{array}{c}m>2\\ m>\frac{1}{2}\end{array}\right.\iff m>2$

Vậy  $\left[\begin{array}{c}m<0\\ m>2\end{array}\right.$

Mà m ∈(−2019; 2019) và m ∈ Z nên m ∈ {−2018; −2017;...; −1; 3; 4;...; 2018}

Số các giá trị của m thỏa mãn bài toán là 2018 + 2016 = 4034.

Đáp án cần chọn là: D

Ta có:  $x^2+\frac{25x^2}{{\left(x+5\right)}^2}=11$$\iff \frac{x^2}{x+5}\left(x+5+\frac{25}{x+5}\right)=11$

$\iff \frac{x^2}{x+5}.\frac{x^2+10x+50}{x+5}=11\iff \frac{x^2}{x+5}\left(\frac{x^2}{x+5}+10\right)=11$

$\iff {\left(\frac{x^2}{x+5}\right)}^2+10\frac{x^2}{x+5}-11=0\iff \left[\begin{array}{c}\frac{x^2}{x+5}=1\\ \frac{x^2}{x+5}=-11\end{array}\right.$

$\iff \left[\begin{array}{c}{x}^2-x-5=0\\ x^2+11x+55=0\left(vn\right)\end{array}\right.\iff \left[\begin{array}{c}x=\frac{1-\sqrt{21}}{2}\approx -1,79\\ x=\frac{1+\sqrt{21}}{2}\approx 2,79\end{array}\right.$

Đáp án cần chọn là: D

Điều kiện  $x\ne 0$

Đặt $t=x+\frac{1}{x}$ suy ra

$t^2=x^2+\frac{1}{x^2}+2\ge 2+2=4\Rightarrow \left|t\right|\ge 2hay1\le -2$ hoặc  $t\ge 2$

Phương trình đã cho trở thành

$t^2-2mt-1+2m=0$, phương trình này luôn có hai nghiệm là  $t_1=1,t_2=2m-1$

Theo yêu cầu của bài toán suy ra  $\left[\begin{array}{c}2m-1\ge 2\\ 2m-1\le -2\end{array}\right.\iff \left[\begin{array}{c}m\ge \frac{3}{2}\\ m\le -\frac{1}{2}\end{array}\right.$

Đáp án cần chọn là: D

Đặt t = x² + 2x + 4 = (x + 1)² + 3 ≥ 3, phương trình trở thành

t² − 2mt + 4m – 1 = 0   (2)

Nhận xét: Ứng với mỗi nghiệm t > 3 của phương trình (2) cho ta hai nghiệm của phương trình (1). Do đó phương trình (1) có đúng hai nghiệm khi phương trình (2) có đúng một nghiệm t > 3

  $\iff \left[\begin{array}{c}\left\{\begin{array}{c}\Delta \text{'}=0\\ x=-\frac{b}{2a}>3\end{array}\right.\\ \left\{\begin{array}{c}\Delta \text{'}>0\\ af\left(3\right)<0\end{array}\right.\end{array}\right.\iff \left[\begin{array}{c}\left\{\begin{array}{c}{m}^2-4m+1=0\\ m>3\end{array}\right.\\ \left\{\begin{array}{c}{m}^2-4m+1>0\\ 1.\left(3^2-2m.3+4m-1\right)<0\end{array}\right.\end{array}\right.$$\iff \left[\begin{array}{c}m=2+\sqrt{3}\\ m>4\end{array}\right.$

Đáp án cần chọn là: A

Điều kiện: x ≠ 0

Phương trình thành (m² + 2)x + 3m = 2x ⇔ m²x = −3m

Vì m ≠ 0 suy ra x =$-\frac{3}{m}$.

Đáp án cần chọn là: C

Điều kiện:  $\left\{\begin{array}{c}x\ne 1\\ x\ne -1\end{array}\right.$

Phương trình (1) trở thành

$\frac{x-m}{x+1}=\frac{x-2}{x-1}$(1) ⇔ (x − m) (x − 1) = (x − 2) (x + 1)

⇔ x² – x – mx + m = x² – x – 2 ⇔ mx = m + 2   (2)

Phương trình (1) có nghiệm duy nhất

⇔ Phương trình (2) có nghiệm duy nhất khác −1 và 1

$\iff \left\{\begin{array}{c}m\ne 0\\ \frac{m+2}{m}\ne 1\\ \frac{m+2}{m}\ne -1\end{array}\right.\iff \left\{\begin{array}{c}m\ne 0\\ m+2\ne m\\ m+2\ne -m\end{array}\right.\iff \left\{\begin{array}{c}m\ne 0\\ 2\ne 0\\ m\ne -1\end{array}\left(ld\right)\iff \left\{\begin{array}{c}m\ne 0\\ m\ne -1\end{array}\right.\right.$

Đáp án cần chọn là: D

Điều kiện: x ≠ 1

Phương trình (1) thành:

$x-2+\frac{x+a}{x-1}=a$ ⇔ x² − 3x + 2 + x + a = ax – a

⇔ x² − (2 + a)x + 2a + 2 = 0  (2)

Phương trình (1) có nghiệm duy nhất.

⇔ Phương trình (2) có nghiệm duy nhất khác 1 hoặc phương trình (2) có 2 nghiệm phân biệt có một nghiệm bằng 1

$\iff \left[\begin{array}{c}\left\{\begin{array}{c}\Delta =0\\ x=-\frac{b}{2a}\ne 1\end{array}\right.\\ \left\{\begin{array}{c}\Delta >0\\ f\left(1\right)=0\end{array}\right.\end{array}\right.\iff \left[\begin{array}{c}\left\{\begin{array}{c}{a}^2-4a-4=0\\ \frac{a+2}{2}\ne 1\end{array}\right.\\ \left\{\begin{array}{c}{a}^2-4a-4>0\\ 1-2-a+2a+2=0\end{array}\right.\end{array}\right.$

$\iff \left[\begin{array}{c}\left\{\begin{array}{c}{a}^2-4a-4=0\\ a+2\ne 2\end{array}\right.\\ \left\{\begin{array}{c}{a}^2-4a-4>0\\ a+1=0\end{array}\right.\end{array}\right.\iff \left[\begin{array}{c}a=2+2\sqrt{2}\\ a=2-2\sqrt{2}\\ a=-1\end{array}\right.$

Với $a=2+2\sqrt{2}$ phương trình có nghiệm là $x=2+\sqrt{2}$

Với $a=2-2\sqrt{2}$ phương trình có nghiệm là $x=2-\sqrt{2}$

Với a = -1 phương trình có nghiệm là:  $\left[\begin{array}{c}x=0\left(n\right)\\ x=1\left(l\right)\end{array}\right.$

Đáp án cần chọn là: D

Ta có:  $\frac{x^2+mx+2}{x^2-1}=1$ $\iff \left\{\begin{array}{c}x\ne \pm 1\\ mx=-3\end{array}\right.$

Phương trình đã cho vô nghiệm  $\Rightarrow \left[\begin{array}{c}m=0\\ \left\{\begin{array}{c}m\ne 0\\ -\frac{3}{m}=\pm 1\end{array}\right.\end{array}\right.\iff \left[\begin{array}{c}m=0\\ m=\pm 3\end{array}\right.$

Đáp án cần chọn là: C

Điều kiện:  $\left\{\begin{array}{c}2x-3\ne 0\\ \left|x+1\right|\ne 0\end{array}\right.\iff \left\{\begin{array}{c}x\ne \frac{3}{2}\\ x\ne -1\end{array}\right.$

Phương trình (1) trở thành:  |x + 1| (x − 1) = (−3x + 1)(2x − 3)

TH1: x ≥ −1

Phương trình thành x² – 1 = −6x² + 11x – 3 ⇔ 7x² − 11x + 2 = 0

$\iff \left[\begin{array}{c}x=\frac{11+\sqrt{65}}{14}\left(n\right)\\ x=\frac{11-\sqrt{65}}{14}\left(n\right)\end{array}\right.$

TH2: x < −1

Phương trình thành -x² + 1 = −6x² + 11x – 3 ⇔ 5x² − 11x + 4 = 0

$\iff \left[\begin{array}{c}x=\frac{11+\sqrt{41}}{10}\left(l\right)\\ x=\frac{11-\sqrt{41}}{10}\left(l\right)\end{array}\right.$ Vậy S =$\left\{\frac{11+\sqrt{65}}{14};\frac{11-\sqrt{65}}{14}\right\}$

Đáp án cần chọn là: D

Điều kiện: x > 2

Ta có:  $\frac{x^2-4x-2}{\sqrt{x-2}}=\sqrt{x-2}$ ⇔ x² − 4x – 2 = x – 2 ⇔ x² − 5x = 0

Vậy S = {5}.

Đáp án cần chọn là: D

Điều kiện x – 2 > 0 ⇔ x > 2.

(1) ⇔ x² − (2m + 3)x + 6m = 0 (2), phương trình luôn có nghiệm là x = 3 và x= 2m

Phương trình (1) có duy nhất 11  nghiệm  $\iff \left[\begin{array}{c}2m\le 2\\ 2m=3\end{array}\right.\iff \left[\begin{array}{c}m\le 1\\ m=\frac{3}{2}\end{array}\right.$

Đáp án cần chọn là: B

Điều kiện:  $x+1\ge 0\iff x\ge -1$

Ta có:

$x+5-4\sqrt{x+1}=x+1-4\sqrt{x+1}+4={\left(\sqrt{x+1}-2\right)}^2$

  $x+2-2\sqrt{x+1}=x+1-2\sqrt{x+1}+1={\left(\sqrt{x+1}-1\right)}^2$

Phương trình:

$\sqrt{x+5-4\sqrt{x+1}}+\sqrt{x+2-2\sqrt{x+1}}=1$

$\iff \left|\sqrt{x+1}-2\right|+\left|\sqrt{x+1}-1\right|\left(1\right)$

+ Trường hợp 1: Nếu $\sqrt{x+1}\ge 2\iff x+1\ge 4\iff x\ge 3$ thì:

$\left\{\begin{array}{c}\left|\sqrt{x+1}-2\right|=\sqrt{x+1}-2\\ \left|\sqrt{x+1}-1\right|=\sqrt{x+1}-1\end{array}\right.$

(1)$\iff$ $\sqrt{x+1}-2$ + $\sqrt{x+1}-1$ =1

    $\iff$$\sqrt{x+1}=2$$\iff x+1=4\iff x=3\left(tm\right)$

+ Trường hợp 2: Nếu $\sqrt{x+1}\le 1\iff x+1\le 1\iff x\le 0$ thì:

$\left\{\begin{array}{c}\left|\sqrt{x+1}-2\right|=2-\sqrt{x+1}\\ \left|\sqrt{x+1}-1\right|=1-\sqrt{x+1}\end{array}\right.$

(1)$\iff 2-\sqrt{x+1}$ + $1-\sqrt{x+1}$=1

    $\iff \sqrt{x+1}=1$$\iff x+1=1\iff x=0\left(tm\right)$

+ Trường hợp 3: Nếu $1<\sqrt{x+1}<2\iff 1<x+1<4\iff 0<x<3$ thì:

$\left\{\begin{array}{c}\left|\sqrt{x+1}-2\right|=2-\sqrt{x+1}\\ \left|\sqrt{x+1}-1\right|=\sqrt{x+1}-1\end{array}\right.$

(1) $\iff 2-\sqrt{x+1}$+ $\sqrt{x+1}-1$=1

$\iff$  1 = 1 (luôn đúng với $\forall x\in (0;3)$)

Vậy tập nghiệm của phương trình là: $\left[0;3\right]$ 

Đáp án cần chọn là: C

Điều kiện:  $\left\{\begin{array}{c}x+3\ge 0\\ 6-x\ge 0\end{array}\right.\iff \left\{\begin{array}{c}x\ge -3\\ x\le 6\end{array}\right.\iff -3\le x\le 6$

Đặt: $\sqrt{x+3}-\sqrt{6-x}=t$

$\iff {(\sqrt{x+3}-\sqrt{6-x})}^2=t^2\iff x+3+6-x-2\sqrt{\left(x+3\right)\left(6-x\right)}=t^2$

$\iff 2\sqrt{\left(x+3\right)\left(6-x\right)}=9-t^2\iff \sqrt{\left(x+3\right)\left(6-x\right)}=\frac{9-t^2}{2}(-3\le t\le 3)$

Khi đó, phương trình trở thành:

$t=3+\frac{9-t^2}{2}\iff t^2+2t-15=0\iff \left[\begin{array}{c}t=3\left(tm\right)\\ t=-5(ktm\end{array}\right.$

Với t = 3 $\Rightarrow \sqrt{x+3}-\sqrt{6-x}=3\iff \sqrt{x+3}=3+\sqrt{6-x}$

$\iff x+3=9+6\sqrt{6-x}+6-x\iff 2x-12=6\sqrt{6-x}\iff x-6=3\sqrt{6-x}$

$\iff \left\{\begin{array}{c}x-6\ge 0\\ x^2-12x+36=9\left(6-x\right)\end{array}\right.\iff \left\{\begin{array}{c}x\ge 6\\ x^2-3x-18=0\end{array}\right.$

$\iff \left\{\begin{array}{c}x\ge 6\\ \left[\begin{array}{c}x=-3\left(l\right)\\ x=6\left(tm\right)\end{array}\right.\end{array}\right.\iff x=6$

Vậy tập nghiệm của phương trình là  $S=\left\{6\right\}$

Đáp án cần chọn là: D

Điều kiện: x² – 6x + 6 ≥ 0 ⇔  $\left[\begin{array}{c}x\le 3-\sqrt{3}\\ x\ge 3+\sqrt{3}\end{array}\right.$

Đặt:$\sqrt{x^2-6x+6}=t$ (t ≥ 0) ⇔ x² − 6x + 6 = t² ⇔ x² − 6x + 9 = t² + 3

Khi đó, phương trình trở thành: ⇔ t² + 3 = 4t ⇔ t² − 4t + 3 = 0 ⇔  $\left[\begin{array}{c}t=1\left(tm\right)\\ t=3\left(tm\right)\end{array}\right.$

+) Với t = 1 ⇒ x² − 6x + 6 = 1 ⇔ x² − 6x + 5 = 0  $\iff \left[\begin{array}{c}x=1\left(tm\right)\\ x=5\left(tm\right)\end{array}\right.$

+) Với t = 3 ⇒ x² − 6x + 6 = 9 ⇒ x² − 6x – 3 = 0  ⇔ $\left[\begin{array}{c}x=3+2\sqrt{3}\left(tm\right)\\ x=3-2\sqrt{3}\left(tm\right)\end{array}\right.$

Vậy phương trình có 4  nghiệm.

Đáp án cần chọn là: C

Điều kiện:  $\left\{\begin{array}{c}x+1\ge 0\\ 3-x\ge 0\\ \sqrt{x+1}+\sqrt{3-x}\ne 0\end{array}\right.\iff \left\{\begin{array}{c}x\ge -1\\ x<3\end{array}\right.\iff -1\le x\le 3$

Đặt: $\sqrt{x+1}+\sqrt{3-x}$= t (t > 0)

$\iff x+1+3-x+2\sqrt{\left(x+1\right)\left(3-x\right)}=t^2$