Trắc nghiệm chuyên đề Toán 8 Chủ đề 11: Hình vuông có đáp án
-
420 lượt thi
-
10 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.
Xem đáp án
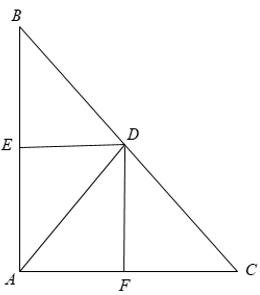
+ Xét tứ giác AEDF có = 900
⇒ AEDF là hình chữ nhật . ( 1 )
Theo giả thiết ta có AD là đường phân giác của góc
⇒ = 450.
+ Xét Δ AED có = 900; = 450 ⇒ = 450
⇒ Δ AED vuông cân tại E nên AE = ED ( 2 )
Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông (dấu hiệu 1 – mục 3)
Câu 2:
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
Xem đáp án
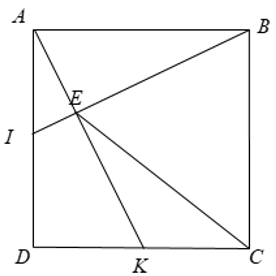
Xét Δ BAI và Δ ADK có:
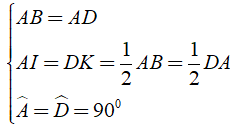
⇒ Δ BAI = Δ ADK ( c - g - c )
⇒ ABIˆ = DAKˆ (góc tương ứng bằng nhau)
Mà = 900 ⇒ = 900
+ Xét Δ ABE có = 1800
⇒ = 1800 - ( ) = 1800 - 900 = 900 hay AK ⊥ BI (đpcm)
Câu 3:
b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
Xem đáp án
+ Xét tứ giác EBCK có = 3600
⇒ = 1800.
Mà = 1800 nên
+ Tứ giác EBCK nội tiếp nên
Mà nên hay tam giác BEC cân tại C
⇒ CE = BC = AB (đpcm)
Câu 4:
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho = 450. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính :
a) Tính số đo = ?
Xem đáp án
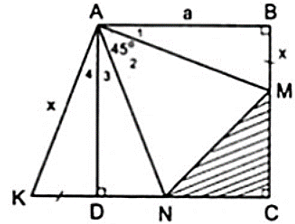
a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
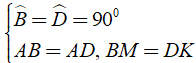
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
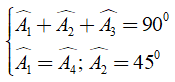
⇒ = 900 - 450 = 450
Câu 5:
b) Chu vi tam giác MCN theo a.
Xem đáp án
b) Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
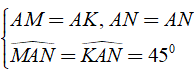
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.
Câu 6:
Xem đáp án
+ Tứ giác có 4 góc vuông là hình chữ nhật
Hình chữ nhật có 4 cạnh bằng nhau là hình vuông.
⇒ Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
Câu 7:
Xem đáp án
+ Trong hình vuông có hai đường chéo vuông góc với nhau, bằng nhau và cắt nhau tại trung điểm mỗi đường
+ Hai đường chéo trong hình vuông đồng thời là trục đối xứng của hình vuông đó.
→ Đáp án B sai.
Câu 8:
Xem đáp án
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
→ Hình bình hành có hai đường chéo bằng nhau thì không là hình vuông.
→ Đáp án D sai.
Câu 9:
Xem đáp án
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
+ Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
+ Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
+ Hình thoi có một góc vuông là hình vuông.
+ Hình thoi có hai đường chéo bằng nhau là hình vuông.
⇒ Hình vuông vừa là hình chữ nhật, cũng vừa là hình thoi.
⇒ Cả 3 phương án đều đúng.
Câu 10:
Xem đáp án
Hình vuông có độ dài cạnh là a ( cm )
Áp dụng định lý Py – to – go thì độ dài đường chéo của hình vuông là a ( cm )
Do đó với a = 4 thì độ dài đường chéo là 4 = ( cm )