Trắc nghiệm chuyên đề Toán 8 Chủ đề 3: Tính chất đường phân giác của tam giác có đáp án
Trắc nghiệm chuyên đề Toán 8 Chủ đề 3: Tính chất đường phân giác của tam giác có đáp án
-
383 lượt thi
-
7 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Hướng dẫn giải:
Áp dụng định lý Py – ta – go ta có: AC = √ (BC2 - AB2) = √ (52 - 32) = 4( cm )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/(DB + DC) = AB/(AB + AC)
hay DB/5 = 3/(3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.
Câu 2:
Xem đáp án
Hướng dẫn giải:
BD là đường phân giác của Δ ABC
Ta có: DA/DC = AB/BC ⇔ DA/(DA + DC) = AB/(AB + BC)
Hay DA/6 = 8/(8 + 10) ⇒ DA = (6.8)/14 = 8/3 ( cm );
Chọn đáp án A.
Câu 3:
Xem đáp án
Hướng dẫn giải:
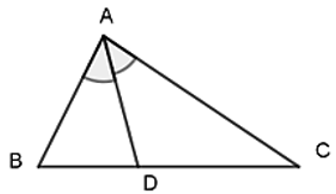
Δ ABC có AD là đường phân giác
Ta có: DB/DC = AB/AC và DC/DB = AC/AB
+ AC là phân giác góc ngoài của Δ ABD
Có: AD/AB = DC/BC
+ AB là phân giác góc ngoài của Δ ADC
Có: AD/AC = BD/BC
Khi đó ta có: AD/AB + AD/AC = DC/BC + DB/BC = 1 ⇒ 1/AB + 1/AC = 1/AD
Chọn đáp án B.
Câu 4:
Xem đáp án
Hướng dẫn giải:
Δ ABC có AD là phân giác trong của góc A.
Ta có: DB/DC = AB/AC ⇒ DB/(BC - DB) = AB/AC
Hay 9/(21 - 9) = 6/x ⇒ x = (12.6)/9 = 8
Chọn đáp án C.
Câu 5:
Xem đáp án
Hướng dẫn giải:
Đường phân giác BACˆ cắt BC tại D
Ta có: DB/DC = AB/AC = 15/20 = 3/4
Chọn đáp án C.
Câu 6:
Cho tam giác ABC vuông tại A, đường phân giác BD. Tính AB, BC biết AD = 4 cm và DC = 5 cm.
Xem đáp án
Hướng dẫn giải:
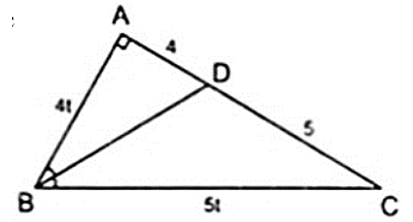
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
với t > 0
Áp dụng định lý Py – ta – go ta có:
BC2 = AC2 + AB2 hay ( 5t )2 = 92 + ( 4t )2 ⇔ ( 3t )2 = 92 ⇒ t = 3 (vì t > 0 )
Khi đó: AB = 12cm, BC = 15cm
Câu 7:
Xem đáp án
Hướng dẫn giải:
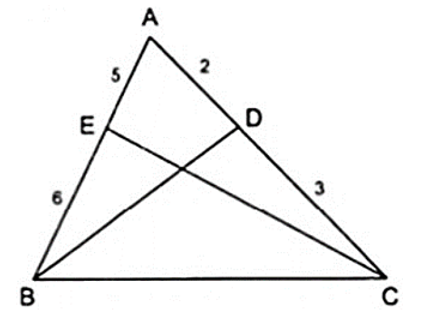
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
với t > 0
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )