Trắc nghiệm chuyên đề Toán 8 Chủ đề 3: Những hằng đảng thức đáng nhớ (có đáp án)
Trắc nghiệm chuyên đề Toán 8 Chủ đề 3: Những hằng đảng thức đáng nhớ (có đáp án)
-
377 lượt thi
-
10 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Tính giá trị của các biểu thức sau:
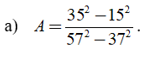
Xem đáp án
a) Ta có:
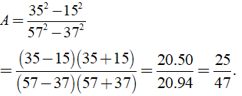
(áp dụng hằng đẳng thức a2 - b2 = ( a + b )( a - b ) )
Vậy A = .
Câu 2:
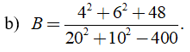
Xem đáp án
b) Ta có
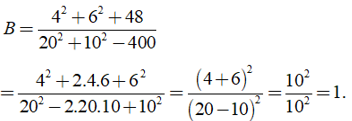
(áp dụng hằng đẳng thức ( a + b )2 = a2 + 2ab + b2; ( a - b )2 = a2 - 2ab + b2 )
Vậy B = 1.
Câu 3:
Tìm x biết
a) ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
Xem đáp án
a) Áp dụng các hằng đẳng thức ( a - b )( a2 + ab + b2 ) = a3 - b3.
( a - b )( a + b ) = a2 - b2.
Khi đó ta có ( x - 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 - x ) = 0.
⇔ x3 - 33 + x( 22 - x2 ) = 0 ⇔ x3 - 27 + x( 4 - x2 ) = 0
⇔ x3 - x3 + 4x - 27 = 0
⇔ 4x - 27 = 0 ⇔ x = .
Vậy giá trị x cần tìm là x= .
Câu 4:
Tìm x biết
b) ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
Xem đáp án
b) Áp dụng hằng đẳng thức ( a - b )3 = a3 - 3a2b + 3ab2 - b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a - b )2 = a2 - 2ab + b2
Khi đó ta có: ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
⇔ ( x3 + 3x2 + 3x + 1 ) - ( x3 - 3x2 + 3x - 1 ) - 6( x2 - 2x + 1 ) = - 10
⇔ 6x2 + 2 - 6x2 + 12x - 6 = - 10
⇔ 12x = - 6 ⇔ x = - 1/2.
Vậy giá trị x cần tìm là x= - 1/2
Câu 5:
Điền vào chỗ trống: A = ( x - y )2 = x2 - ... + y2
Xem đáp án
Áp dụng hằng đẳng thức ( a + b )2 = a2 + 2ab + b2.
Khi đó ta có A = ( x - y )2 = x2 - 2.x.y + y2 = x2 - xy + y2.
Suy ra chỗ trống cần điền là xy.
Chọn đáp án B.
Câu 6:
Xem đáp án
b) Áp dụng hằng đẳng thức ( a - b )3 = a3 - 3a2b + 3ab2 - b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a - b )2 = a2 - 2ab + b2
Khi đó ta có: ( x + 1 )3 - ( x - 1 )3 - 6( x - 1 )2 = - 10.
⇔ ( x3 + 3x2 + 3x + 1 ) - ( x3 - 3x2 + 3x - 1 ) - 6( x2 - 2x + 1 ) = - 10
⇔ 6x2 + 2 - 6x2 + 12x - 6 = - 10
⇔ 12x = - 6 ⇔ x = - .
Vậy giá trị x cần tìm là x= -
Câu 7:
Xem đáp án
Áp dụng hằng đẳng thức a3 - b3 = ( a - b )( a2 + ab + b2 )
Khi đó ta có ( 2x - 1 )( 4x2 + 2x + 1 ) = ( 2x - 1 )[ ( 2x )2 + 2x.1 + 1 ] = ( 2x )3 - 1 = 8x3 - 1.
Suy ra chỗ trống cần điền là 8x3 - 1.
Chọn đáp án D.
Câu 8:
Tính giá trị cuả biểu thức A = 8x3 + 12x2y + 6xy2 + y3 tại x = 2 và y = -1.
Xem đáp án
Áp dụng hằng đẳng thức ( a + b )3 = a3 + 3a2b + 3ab2 + b3.
Khi đó ta có:
A = 8x3 + 12x2y + 6xy2 + y3 = ( 2x )3 + 3.( 2x )2.y + 3.( 2x ).y2 + y3 = ( 2x + y )3
Với x = 2 và y = -1 ta có A = ( 2.2 - 1 )3 = 33 = 27.
Chọn đáp án C.
Câu 9:
Tính giá trị của biểu thức A = 352 - 700 + 102.
Xem đáp án
Ta có A = 352 - 700 + 102 = 352 - 2.35.10 + 102
Áp dụng hằng đẳng thức ( a - b )2 = a2 - 2ab + b2.
Khi đó A = ( 35 - 10 )2 = 252.
Chọn đáp án A.
Câu 10:
Giá trị của x thỏa mãn 2x2 - 4x + 2 = 0 là ?
Xem đáp án
Ta có 2x2 - 4x + 2 = 0 ⇔ 2( x2 - 2x + 1 ) = 0 ( 1 )
Áp dụng hằng đẳng thức ( a - b )2 = a2 - 2ab + b2
Khi đó ta có ( 1 ) ⇔ 2( x - 1 )2 = 0 ⇔ x - 1 = 0 ⇔ x = 1.
Chọn đáp án A.