Trắc nghiệm chuyên đề Toán 8 Chủ đề 5: Đối xứng trục có đáp án (Đề 1)
-
464 lượt thi
-
7 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Chứng minh rằng:
a) D đối xứng với E qua AH.
Xem đáp án
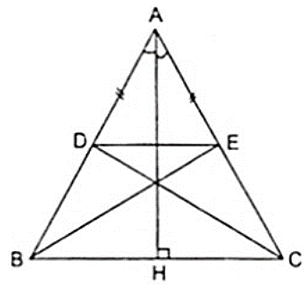
a) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là đường phân giác của góc A.
Theo giả thiết ta có AD = AE nên Δ ADE cân tại A nên AH là đường trung trực của DE
⇒ D đối xứng với E qua AH.
Câu 2:
b) Δ ADC đối xứng với Δ AEB qua AH.
Xem đáp án
b) Vì Δ ABC cân tại A có AH là đường cao theo giả thiết nên AH cũng là trung trực của BC.
⇒ B đối xứng với C qua AH, E đối xứng với D qua AH.
Mặt khác, ta có A đối xứng với A qua AH theo quy ước.
⇒ Δ ADC đối xứng với Δ AEB qua AH.
Câu 3:
Cho Δ ABC có = 500, điểm M thuộc cạnh BC. Vẽ điểm D đối xứng với M qua AB, vẽ điểm E đối xứng với M qua AC.
a) Chứng minh rằng AD = AE.
Xem đáp án
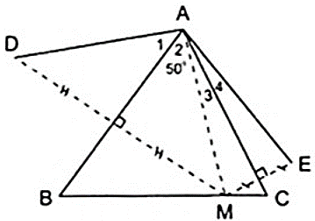
a) Theo giả thiết ta có:
+ D đối xứng với M qua AB.
+ E đối xứng với M qua AC.
+ A đối xứng với A qua AB, AC.
⇒ AD đối xứng với AM qua AB, AE đối xứng với AM qua AC.
Áp dụng tính chất đối xứng ta có:
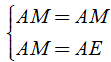
⇒ AD = AE ⇒ (đpcm).
Câu 4:
b) Tính số đo góc = ?
Xem đáp án
b) Theo ý câu a, ta có
+ đối xứng qua AB
+ đối xứng qua AC.
Áp dụng tính chất đối xứng trục, ta có:
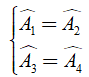
⇒ = = 500 ⇒ = 2 = 1000.
Vậy = 1000.
Câu 5:
Xem đáp án
Định lí: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Câu 6:
Xem đáp án
Tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Khi đó AB = A'B' = 3cm
Câu 7:
Xem đáp án
Tính chất: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
Khi đó ta có: PABC = PA'B'C' = 48( cm )