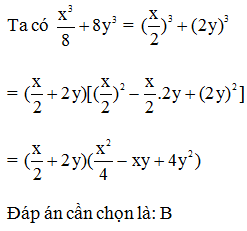Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức có đáp án
Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức có đáp án (Nhận biết)
-
1830 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phân tích đa thức x3y3 + 6x2y2 + 12xy + 8 thành nhân tử ta được
Xem đáp án
Ta có x3y3 + 6x2y2 + 12xy + 8
= (xy)3 + 3(xy)2.2 + 3xy.22 + 23 = (xy + 2)3
Đáp án cần chọn là: A
Câu 2:
Phân tích đa thức 8x3 + 12x2y + 6xy2 + y3 thành nhân tử ta được
Xem đáp án
Ta có 8x3 + 12x2y + 6xy2 + y3
= (2x)3 + 3.(2x)2y + 3.2x.y2 + y3 = (2x + y)3
Đáp án cần chọn là: B
Câu 3:
Chọn câu đúng.
Xem đáp án
Ta có (5x – 4)2 – 49x2 = (5x – 4)2 – (7x)2
= (5x – 4 + 7x)(5x – 4 – 7x)
= (12x – 4)(-2x – 4) = 4.(3x – 1).(-2)(x + 2)
= -8(3x – 1)(x + 2)
Đáp án cần chọn là: D
Câu 4:
Chọn câu đúng.
Xem đáp án
Ta có (3x – 2y)2 – (2x – 3y)2 = (3x – 2y + 2x – 3y)(3x – 2y – (2x – 3y))
= (5x – 5y)(3x – 2y – 2x + 3y) = 5(x – y)(x + y)
Đáp án cần chọn là: A
Câu 5:
Chọn câu sai.
Xem đáp án
Ta có
+) 4x2 + 4x + 1 = (2x)2 + 2.2x.1 + 12 = (2x + 1)2 nên A đúng
+) 9x2 – 24xy + 16y2 = (3x)2 – 2.3x.4y + (4y)2 = (3x – 4y)2 nên B đúng
+) nên C đúng, D sai
Đáp án cần chọn là: D
Câu 6:
Chọn câu sai.
Xem đáp án
Ta có
+) x2 – 6x + 9 = x2 – 2.3x + 32 = (x – 3)2 nên A đúng
+) 4x2 – 4xy + y2 = (2x)2 – 2.2x.y + y2 = (2x – y)2 nên B đúng
+) nên C đúng
+) -x2 – 2xy – y2 = -(x2 + 2xy + y2) = -(x + y)2 nên D sai
Đáp án cần chọn là: D
Câu 7:
Phân tích (a2 + 9)2 – 36a2 thành nhân tử ta được
Xem đáp án
Ta có (a2 + 9)2 – 36a2 = (a2 + 9)2 – (6a)2
= (a2 + 9 + 6a)(a2 + 9 – 6a) = (a + 3)2(a – 3)2
Đáp án cần chọn là: A
Câu 8:
Cho 8x3 – 64 = (2x – 4)(…). Biểu thức thích hợp điền vào dấu … là
Xem đáp án
Ta có 8x3 – 64 = (2x)3 – 43 = (2x – 4)(4x2 + 8x + 16)
Đáp án cần chọn là: D
Câu 9:
Cho 27x3 – 0,001 = (3x – 0,1)(..). Biểu thức thích hợp điền vào dấu … là
Xem đáp án
Ta có 27x3 – 0,001 = (3x)3 – (0,1)3 = (3x – 0,1)((3x)2 + 3x.0,1 + 0,12)
= (3x – 0,1)(9x2 + 0,3x + 0,01)
Đáp án cần chọn là: C
