Trắc nghiệm chuyên đề Toán 8 Chủ đề 5. Diện tích hình thoi có đáp án
-
301 lượt thi
-
6 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
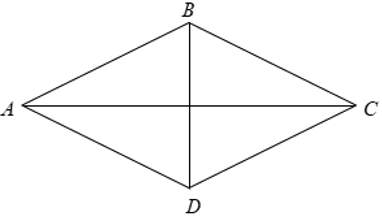
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HA = HC = 5( cm )
Áp dụng định lí Py – to – go ta có:
AB2 = AH2 + HB2 ⇒ BH = √ (AB2 - AH2)
⇒ HB = √ (132 - 52) = 12( cm )
⇒ BD = HB + HD = 2HB = 2.12 = 24( cm )
Khi đó ta có SABCD = AC.BD = .10.24 = 120( cm2 ).
Vậy diện tích của hình thoi là 120( cm2 )
Câu 2:
Xem đáp án
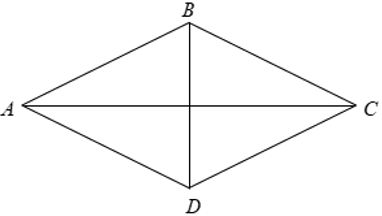
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46( cm )
⇔ ( HB + HD ) + ( HC + HA ) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có: HA + HB = 23 ⇔ ( HA + HB )2 = 232
⇔ HA2 + 2HA.HB + HB2 = 232 ( 1 )
Mặt khác, theo định lí Py–ta–go ta có: AH2 + HB2 = AB2 = 172 ( 2 )
Từ ( 1 ) và ( 2 ) ta có: 172 + 2HA.HB = 232 ⇒ HA.HB = = 120.
Hay = 120 ⇔ .AC.BD = 240 ⇒ SABCD = 240( cm2 )
Vậy diện tích hình thoi là 240cm2.
Câu 3:
Xem đáp án
Chọn đáp án B.
Diện tích của hình thoi là S = d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = .8.10 = 40( cm2 )
Câu 4:
Xem đáp án
Chọn đáp án C.
Diện tích của hình thoi là S = d1.d2
Trong đó d1,d2 lần lượt là độ dài hai đường chéo.
Khi đó, diện tích của hình thoi là Shình thoi = .a√ 2 . a√ 3 = ( cm2 )
Câu 5:
Xem đáp án
Chọn đáp án B.
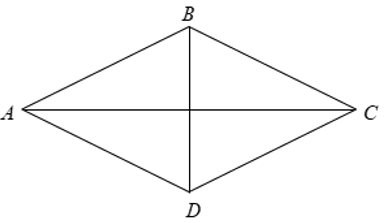
Xét hình thoi ABCD có BACˆ = 600.
Ta có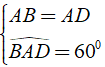 
⇒ Δ ABD đều.
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py–ta–go ta có:
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2)
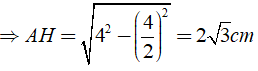
⇒ AC = 2AH = 4√ 3 ( cm )
Do đó SABCD = AC.BD = .4√ 3 .4 = 8√ 3 ( cm2 )
Câu 6:
Xem đáp án
Chọn đáp án C.
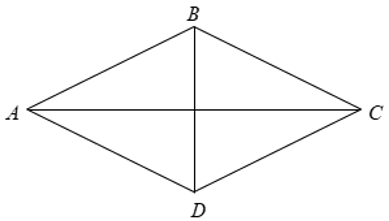
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HB = HD = 4 (cm)
Theo giải thiết ta có:
PABCD = AB + BC + CD + DA = 40
⇒ AB = BC = CD = DA = 10 (cm)
Áp dụng định lý Py – ta – go ta có :
AH2 + HB2 = AB2 ⇒ AH = √ (AB2 - HB2) = √ (102 - 42) = 2√ 21 (cm)
⇒ AC = 2AH = 4√ 21 (cm)
Do đó SABCD = .BD.AC = .4√ (21) .8 = 16√ 21 (cm2)