Trắc nghiệm chuyên đề Toán 8 Chủ đề 3. Diện tích tam giác có đáp án
-
212 lượt thi
-
6 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
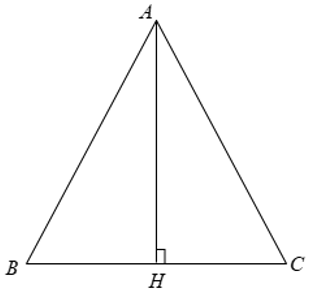
Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC =
Khi đó ta có: SABC =
Áp dụng định lý Py – to – go ta có:
AC2 = AH2 + HC2 ⇒ AH =
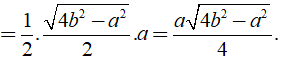
Khi đó SABC =
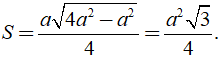
Do đó diện tích của tam giác đều các cạnh bằng a là
Câu 2:
Cho Δ ABC cân tại A có BC = 30cm, đường cao AH = 20cm. Tính đường cao ứng với cạnh bên của tam giác cân đó.
Xem đáp án
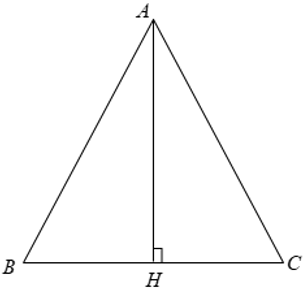
Xét Δ ABC cân tại A có BC = 30( cm )
⇒ BH = CH = 15( cm ).
Áp dụng đinh lý Py – ta – go ta có:
AB = = 25( cm )
Kẻ BK ⊥ AC, giờ ta phải tính BK = ?
Ta có : SABC = AH.BC = .20.30 = 300 ( cm2 )
Mặt khác SABC = .BK.AC = .BK.25
Do đó, ta có .BK.25 = 300 ⇔ BK = = 24( cm ).
Câu 3:
Xem đáp án
Chọn đáp án C.
Ta có diện tích của tam giác: S = b.h.
Trong đó: b là độ dài cạnh đáy, h là độ dài đường cao
Khi đó ta có : S = .AH.BC = BC.BC = .BC2.
Câu 4:
Xem đáp án
Chọn đáp án B.
Câu 5:
Xem đáp án
Chọn đáp án C.
Áp dụng định lý Py – to – go ta có: AB2 + AC2 = BC2 ⇒ AC = √ (BC2 - AB2)
⇒ AC = √ (52 - 42) = 3cm.
Khi đó SABC = AB.AC = .4.3 = 6( cm2 )
Câu 6:
Xem đáp án
Chọn đáp án A.
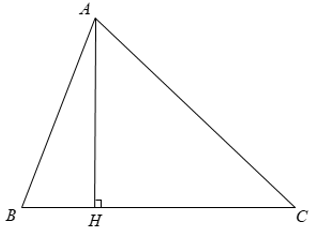
Áp dụng định lý Py – to – go ta có:
+ Xét Δ ABH có AH2 + BH2 = AB2 ⇒ AH = √ (AB2 - BH2)
⇒ AH = √ (152 - 122) = 9 ( cm ).
+ Xét Δ ACH có AC2 = AH2 + HC2 ⇒ HC = √ (AC2 - AH2)
⇒ HC = √ (412 - 92) = 40 ( cm ).
Khi đó SABC = AH.BC = AH( HB + HC ) = .9.( 12 + 40 ) = 234 ( cm2 ).